A természetben előforduló és az ember által előállított szilárd anyagok több mint 90%-a kristályos. A legtöbb szilárd anyag részecskéinek szabályos elrendeződésével alakul ki, mert a részecskék közötti összes vonzó kölcsönhatás maximális, és a teljes intermolekuláris energia minimális, amikor a részecskék a leghatékonyabb módon pakolódnak. Az atomi szintű szabályos elrendeződés gyakran makroszkopikus szinten is tükröződik. Ebben a modulban a fémes és ionos kristályos szilárd testek szerkezetének néhány részletét tárjuk fel, és megtanuljuk, hogyan határozzák meg ezeket a szerkezeteket kísérletileg.

A fémek szerkezete

A kristályos szilárd testek tárgyalását az elemi fémek vizsgálatával kezdjük, amelyek viszonylag egyszerűek, mivel mindegyik csak egyféle atomot tartalmaz. A tiszta fém olyan kristályos szilárd anyag, amelyben a fématomok ismétlődő mintázatban szorosan egymás mellé vannak pakolva. A fémek néhány általános tulajdonsága, mint például az alakíthatóság és a képlékenység, nagyrészt annak köszönhető, hogy az azonos atomok szabályos mintázatban helyezkednek el. Az egyik fémnek a másiktól eltérő tulajdonságai részben az atomok méretétől és térbeli elrendezésük sajátosságaitól függnek. A következő fejezetekben négy leggyakoribb fémkristálygeometria hasonlóságait és különbségeit vizsgáljuk meg.

A fémek egységcellái

A kristályos szilárd anyag – legyen az fém vagy sem – szerkezetét legjobban úgy írhatjuk le, ha a legegyszerűbb ismétlődő egységét tekintjük, amelyet egységcellának nevezünk. Az egységcella rácspontokból áll, amelyek az atomok vagy ionok helyét képviselik. A teljes szerkezet ezután ebből a három dimenzióban ismétlődő egységcellából áll, amint azt az 1. ábra szemlélteti.

1. ábra. Az egységcella a minden irányban ismétlődő rácspontok helyét mutatja.

A kristályok rácsszerkezetének és egységcelláinak vizsgálatát kezdjük a legegyszerűbb szerkezettel és a legegyszerűbb egységcellával. Ennek szemléltetésére képzeljük el, hogy veszünk nagyszámú egyforma gömböt, például teniszlabdát, és egyenletesen elrendezzük őket egy edényben. Ennek legegyszerűbb módja az lenne, ha olyan rétegeket hoznánk létre, amelyekben az egyik rétegben lévő gömbök közvetlenül az alatta lévő rétegben lévők felett helyezkednek el, ahogyan azt a 2. ábra szemlélteti. Ezt az elrendezést egyszerű köbös szerkezetnek, az egységcellát pedig egyszerű köbös egységcellának vagy primitív köbös egységcellának nevezzük.

2. ábra. Ha a fématomok úgy vannak elrendezve, hogy az egyik rétegben lévő gömbök közvetlenül egy másik rétegben lévő gömbök felett vagy alatt helyezkednek el, a rácsszerkezetet egyszerű köbösnek nevezzük. Vegyük észre, hogy a gömbök érintkeznek.

Az egyszerű köbös szerkezetben a gömbök nincsenek olyan szorosan egymás mellé pakolva, mint ahogyan lehetne, és a tartály térfogatának csak mintegy 52%-át “töltik ki”. Ez egy viszonylag gazdaságtalan elrendeződés, és csak egy fém (polónium, Po) kristályosodik egyszerű köbös szerkezetben. Amint a 3. ábrán látható, egy ilyen elrendezésű szilárd anyag olyan síkokból (vagy rétegekből) áll, amelyekben minden atom csak a négy legközelebbi szomszédjával érintkezik a saját rétegében; egy atom közvetlenül fölötte a fölötte lévő rétegben; és egy atom közvetlenül alatta az alatta lévő rétegben. A kristályos szilárd anyagban az egyes részecskék által a többi részecskével érintkező részecskék számát koordinációs számnak nevezzük. Egy polónium atom esetében egy egyszerű köbös elrendezésben a koordinációs szám tehát hat.

3. ábra. Egy egyszerű köbös rácsszerkezetben egy atom hat másik atommal érintkezik, így koordinációs száma hat.

Az egyszerű köbös rácsban a minden irányban ismétlődő egységcella egy nyolc atom középpontja által meghatározott kocka, amint az a 4. ábrán látható. Ennek az egységcellának a szomszédos sarkaiban lévő atomok érintkeznek egymással, így ennek a cellának az élhossza két atomsugárral, azaz egy atomátmérővel egyenlő. A köbös egységcella csak ezen atomok azon részeit tartalmazza, amelyek benne vannak. Mivel egy egyszerű köbös egységcella egyik sarkában lévő atomot összesen nyolc egységcella tartalmazza, ennek az atomnak csak egy nyolcada van egy adott egységcellán belül. És mivel minden egyes egyszerű köbös egységcellának mind a nyolc “sarkában” van egy-egy atom, egy egyszerű köbös egységcellán belül 8 \times \frac{1}{8}=1 atom van.

4. ábra. Egy egyszerű kocka rácsos egységcella mind a nyolc sarkában egy-egy atom nyolcadát tartalmazza, tehát összesen egy atomot tartalmaz.

1. példa: Atomsugár és sűrűség számítása fémeknél, 1. rész

Az alfa-polónium egységcellájának élhossza 336 pm.

1. Meghatározzuk a polónium atom sugarát.
2. Meghatározzuk az alfa-polónium sűrűségét.

Megoldás megjelenítése

Az alfa-polónium egyszerű kocka egységcellában kristályosodik:

1. Két szomszédos Po atom érintkezik egymással, így ennek a cellának az élhossza egyenlő két Po atom sugarával: l=2r. Ezért a Po sugara r=\dfrac{\text{l}}{2}=\dfrac{\text{336 pm}}{2}=\text{168 pm}.
2. A sűrűséget a \text{sűrűség}=\dfrac{\text{tömeg}}{\text{térfogat}} adja. A polónium sűrűsége az egységcellájának sűrűségét (az egységcellában található tömeg osztva az egységcella térfogatával) meghatározva állapítható meg. Mivel egy Po egységsejt mind a nyolc sarkában egy nyolcad Po atomot tartalmaz, egy egységsejt egy Po atomot tartalmaz.

A Po egységsejt tömege a következő módon határozható meg:

\text{1 Po egységsejt}\times \dfrac{\text{1 Po atom}}{\text{1 Po egységsejt}}\times \dfrac{\text{1 mol Po}}{6.022\times {10}^{23}\text{Po atomok}}\times \dfrac{208.998\text{g}}{\text{1 mol Po}}=3.47\times {10}^{-22}\text{g}

A Po egységcella térfogata a következőképpen határozható meg:

V={l}^{3}={(336\times {10}^{-10}\text{cm})}^{3}=3.79\times {10}^{-23}{\text{cm}}^{3}

(Megjegyzendő, hogy az élhosszúságot pm-ről cm-re számoltuk át, hogy megkapjuk a sűrűség szokásos térfogategységét.)

Ezért a sűrűség \text{Po}=\dfrac{3.471\times {10}^{-22}\text{g}}{3.79\times {10}^{-23}{\text{cm}}^{3}}={\text{9.16 g/cm}}^{3}

Check Your Learning

A nikkel egységcellájának élhossza 0,3524 nm. A Ni sűrűsége 8,90 g/cm3 . A nikkel egyszerű köbös szerkezetben kristályosodik? Magyarázza meg.

Megoldás megjelenítése

Nem. Ha a Ni egyszerű köbös lenne, akkor a sűrűsége a következő lenne:

\text{1 Ni atom}\times \dfrac{\text{1 mol Ni}}{6.022\times {10}^{23}\text{Ni atomok}}\times \dfrac{58.693\text{g}}{\text{1 mol Ni}}=9.746\times {10}^{-23}\text{g}
V={l}^{3}={(3.524\times {10}^{-8}\text{cm})}^{3}=4.376\times {10}^{-23}{\text{cm}}^{3}

Ezután a Ni sűrűsége =\dfrac{9.746\times {10}^{-23}\text{g}}{4.376\times {10}^{-23}{\text{cm}}^{3}}={\text{2.23 g/cm}}^{3}

Mivel a Ni tényleges sűrűsége nem közelíti meg ezt, a Ni nem alkot egyszerű köbös szerkezetet.

A legtöbb fémkristály a négy fő egységcellatípus valamelyikét alkotja. Egyelőre a három köbös egységcellára összpontosítunk: az egyszerű köbösre (amelyet már láttunk), a testközpontú köbös egységcellára és az arcközpontú köbös egységcellára – mindegyiket az 5. ábra szemlélteti. (Megjegyezzük, hogy valójában hét különböző rácsrendszer létezik, amelyek közül néhánynak egynél több rácstípusa van, így összesen 14 különböző típusú egységcella létezik. A bonyolultabb geometriákat későbbre hagyjuk ebben a modulban.)

5. ábra. A fémek köbös egységcellái (a felső ábrákon) a rácspontok helyét, és (az alsó ábrákon) az egységcellában elhelyezkedő fématomokat mutatják.

Néhány fém olyan elrendezésben kristályosodik, amelynek köbös egységcellája minden sarkon atomokkal és egy atommal a középpontban van, ahogy a 6. ábrán látható. Ezt nevezzük testközpontú köbös (BCC) szilárdtestnek. A BCC egységcella sarkaiban lévő atomok nem érintkeznek egymással, hanem a középpontban lévő atommal érintkeznek. Egy BCC egységcella két atomot tartalmaz: a nyolc sarok mindegyikében egy-egy atom nyolcadát ( 8\times \frac{1}{8}=1 atom a sarkokból), valamint egy atomot a középpontból. Ebben a szerkezetben bármely atom négy atomot érint a felette lévő rétegben és négy atomot az alatta lévő rétegben. Így egy BCC szerkezetben lévő atom koordinációs száma nyolc.

6. ábra. Testközpontú kockaszerkezetben az adott rétegben lévő atomok nem érnek egymáshoz. Minden atom négy atomot érint a felette lévő rétegben és négy atomot az alatta lévő rétegben.

A BCC elrendezésben az atomok sokkal hatékonyabban vannak elhelyezve, mint egy egyszerű köbös szerkezetben, a teljes térfogat mintegy 68%-át foglalják el. A BCC szerkezetű izomorf fémek közé tartozik a K, Ba, Cr, Mo, W és Fe szobahőmérsékleten. (Az azonos szerkezetben kristályosodó elemeket vagy vegyületeket izomorfnak nevezzük.)

Sok más fém, például az alumínium, a réz és az ólom olyan elrendezésben kristályosodik, amely kockaelemes egységcellával rendelkezik, amelynek minden sarkában és minden oldal középpontjában atomok vannak, amint azt a 7. ábra szemlélteti. Ezt az elrendezést nevezzük arcközpontú köbös (FCC) szilárdtestnek. Egy FCC egységcella négy atomot tartalmaz: egy nyolcad atomot mind a nyolc sarkon ( 8\times \frac{1}{8}=1 atom a sarkoktól) és egy fél atomot mind a hat felületen (6\times \frac{1}{2}=3 atom a felületektől). A sarkok atomjai a kocka átlói mentén érintkeznek a szomszédos oldalak középpontjában lévő atomokkal. Mivel az atomok azonos rácspontokon állnak, azonos környezetük van.

7. ábra. Az arcközpontú köbös szilárd testben az atomok a sarkokban és, ahogy a neve is mutatja, az egységcellák oldalainak középpontjában helyezkednek el.

Az FCC elrendezésben az atomok a lehető legszorosabban vannak egymás mellé pakolva, az atomok a térfogat 74%-át foglalják el. Ezt a szerkezetet a legszorosabb köbös pakolásnak (CCP) is nevezik. A CCP-ben három ismétlődő rétegben hexagonálisan elrendezett atomok találhatók. Minden atom hat atommal érintkezik a saját rétegében, hárommal a felette lévő rétegben és hárommal az alatta lévő rétegben. Ebben az elrendezésben minden atom 12 közeli szomszédjával érintkezik, ezért koordinációs száma 12. Az, hogy az FCC és a CCP elrendezések egyenértékűek, talán nem tűnik fel azonnal, de hogy valójában miért ugyanaz a szerkezet, azt a 8. ábra szemlélteti.

A 8. ábra. A CCP elrendezés három ismétlődő rétegből (ABCABC…) áll, amelyek hatszögletűen elrendezett atomokból állnak. A CCP-szerkezetben az atomok koordinációs száma 12, mivel hat atomot érintkeznek a saját rétegükben, plusz három atomot a felette lévő rétegben és három atomot az alatta lévő rétegben. Ha elforgatjuk a perspektívánkat, láthatjuk, hogy a CCP-szerkezet egy olyan egységcellával rendelkezik, amelynek egyik oldala az egyik sarkában egy atomot tartalmaz az A rétegből, a B réteg atomjait az átló mentén (két sarkon és az oldal közepén), és egy atomot a C rétegből a fennmaradó sarkon. Ez megegyezik az arcközpontú köbös elrendezéssel.

Miatt a szorosabb elrendeződés maximalizálja az atomok közötti összes vonzást és minimalizálja a teljes molekulák közötti energiát, a legtöbb fémben az atomok így helyezkednek el. Az egyszerű fémes kristályszerkezetekben a legszorosabb pakolás két típusát találjuk: A CCP-t, amellyel már találkoztunk, és a 9. ábrán látható hexagonális legszorosabb csomagolást (HCP). Mindkettő hexagonálisan elrendezett atomok ismétlődő rétegeiből áll. Mindkét típusban az első rétegre (A) egy második réteg (B) kerül úgy, hogy a második réteg minden atomja az első réteg három atomjával érintkezik. A harmadik réteget kétféleképpen lehet elhelyezni. A HCP-ben a harmadik réteg atomjai közvetlenül az első réteg atomjai felett helyezkednek el (azaz a harmadik réteg is A-típusú), és az egymásra rétegződés A és B-típusú, szorosan pakolt rétegek váltakozásából áll (azaz ABABAB⋯). A CCP esetében a harmadik réteg atomjai nem helyezkednek el az első két réteg egyikének atomjai felett sem (azaz a harmadik réteg C típusú), és a rétegrend váltakozó A, B és C típusú szorosan pakolt rétegekből áll (azaz ABCABCABCABC⋯). A fémek mintegy kétharmada 12-es koordinációs számú, legszorosabban pakolt rétegsorokban kristályosodik. A HCP szerkezetben kristályosodó fémek közé tartozik a Cd, Co, Li, Mg, Na és Zn, a CCP szerkezetben kristályosodó fémek közé pedig az Ag, Al, Ca, Cu, Ni, Pb és Pt.

2. példa: Atomsugár és sűrűség számítása fémeknél, 2. rész

A kalcium arcközpontú köbös szerkezetben kristályosodik. Egységcellájának élhossza 558,8 pm.

1. Mi a Ca atomsugara ebben a szerkezetben?
2. Kalkulálja ki a Ca sűrűségét.

Megoldás megjelenítése

1. rész

A FCC szerkezetben a Ca atomok a felület átlóján keresztül érintkeznek egymással, így az átló hossza négy Ca atomi sugárral egyenlő (d = 4r). Két szomszédos él és az arc átlója derékszögű háromszöget alkot, amelynek minden oldalának hossza 558,8 pm, a hipotenzus hossza pedig négy Ca atomsugárral egyenlő:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}\longrightarrow {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}}{16}}=\text{197.6 pmg egy Ca sugárra}.

2. rész

A sűrűséget \text{sűrűség}=\dfrac{\text{tömeg}}{\text{térfogat}} adja. A kalcium sűrűségét úgy találhatjuk meg, hogy meghatározzuk az egységcellájának sűrűségét: például az egységcellában található tömeg osztva az egységcella térfogatával. Egy arcközpontú Ca egységcella mind a nyolc sarkán \left(8\times \dfrac{1}{8}=1\text{ atom}\right) egy-egy nyolcad atom van, és egy-egy fél atom a hat oldal mindegyikén \left(6\times \dfrac{1}{2}=3\text{ atom}\right), tehát összesen négy atom van az egységcellában.

Az egységcella tömege a következőképpen határozható meg:

\text{1 Ca egységcella}\times \dfrac{\text{4 Ca atom}}{\text{1 Ca egységcella}}\times \dfrac{\text{1 mol Ca}}{6.022\times {10}^{23}\text{Ca-atomok}}\times \dfrac{40.078\text{g}}{\text{1 mol Ca}}=2.662\times {10}^{-22}\text{g}

A Ca egységcellájának térfogata a következőképpen határozható meg:

V={a}^{3}={(558.8\times {10}^{-10}\text{cm})}^{3}=1.745\times {10}^{-22}{\text{cm}}^{3}

(Megjegyzendő, hogy az élhosszúságot pm-ről cm-re számoltuk át, hogy a sűrűség szokásos térfogategységét kapjuk.)

Az \text{Ca}=\dfrac{2.662\times {10}^{-22}\text{g}}{1.745\times {10}^{-22}{\text{cm}}}^{3}}={\text{1.53 g/cm}}^{3}

Check Your Learning

Az ezüst FCC szerkezetben kristályosodik. Egységcellájának élhossza 409 pm.

1. Melyik az Ag atomsugara ebben a szerkezetben?
2. Kalkulálja ki az Ag sűrűségét.

Megoldások megjelenítése

1. 144 pm
2. 10.5 g/cm3

Az egységcellát általában három tengely (a, b és c) hossza és a köztük lévő szögek (α, β és γ) határozzák meg, amint azt a 10. ábra szemlélteti. A tengelyeket úgy határozzuk meg, mint a térrács pontjai közötti hosszakat. Következésképpen az egységcellák tengelyei azonos környezetű pontokat kötnek össze.

10. ábra. Egy egységcellát a három tengelyének (a, b és c) hossza és a tengelyek közötti szögek (α, β és γ) határozzák meg.

Hét különböző rácsrendszer létezik, amelyek közül néhány több rácstípust is tartalmaz, így összesen tizennégy különböző egységcellát, amelyek a 11. ábrán látható alakúak.

11. ábra. Hét különböző rácsrendszer és 14 különböző egységcella létezik.

Az ionos kristályok szerkezete

Az ionos kristályok két vagy többféle, általában különböző méretű ionból állnak. Ezeknek az ionoknak a kristályszerkezetbe való pakolása bonyolultabb, mint az azonos méretű fématomoké.

A legtöbb egyatomos ion töltött gömbként viselkedik, és az ellentétes töltésű ionok iránti vonzása minden irányban azonos. Következésképpen az ionos vegyületek stabil szerkezete akkor jön létre, (1) ha az egy töltéssel rendelkező ionokat a lehető legtöbb ellentétes töltésű ion veszi körül, és (2) ha a kationok és anionok érintkeznek egymással. A szerkezeteket két fő tényező határozza meg: az ionok relatív mérete és a vegyületben lévő pozitív és negatív ionok számának aránya.

12. ábra felirat jelöli. A kationok kétféle lyukat foglalhatnak el az anionok között: oktaéderes lyukakat vagy tetraéderes lyukakat.

Az egyszerű ionos szerkezetekben általában az anionokat, amelyek általában nagyobbak, mint a kationok, a legszorosabb elrendezésben találjuk. (Mint korábban láttuk, az azonos atommaghoz vonzott több elektron az anionokat nagyobbá, az azonos atommaghoz vonzott kevesebb elektron pedig a kationokat kisebbé teszi azokhoz az atomokhoz képest, amelyekből képződnek.) A kisebb kationok általában az anionok között megmaradó kétféle lyuk (vagy rés) egyikét foglalják el. A kisebbik lyuk az egyik síkban három anion és egy szomszédos síkban egy anion között található. Az ezt a lyukat körülvevő négy anion egy tetraéder sarkaiban helyezkedik el, ezért a lyukat tetraéderes lyuknak nevezzük. A nagyobb lyuk típus egy oktaéder sarkaiban elhelyezkedő hat anion (három az egyik síkban és három a szomszédos síkban) középpontjában található; ezt nevezzük oktaéderes lyuknak. A 12. ábra mindkét lyuktípust szemlélteti.

A kationok és anionok relatív méretétől függően egy ionos vegyület kationjai tetraéderes vagy oktaéderes lyukakat foglalhatnak el, amint azt a 13. ábra szemlélteti. A viszonylag kis kationok tetraéderes lyukakat, a nagyobb kationok pedig oktaéderes lyukakat foglalnak el. Ha a kationok túl nagyok ahhoz, hogy beférjenek az oktaéderes lyukakba, az anionok egy nyitottabb szerkezetet, például egy egyszerű köbös elrendezést vehetnek fel. A nagyobb kationok ekkor elfoglalhatják a nyitottabb térköz által lehetővé tett nagyobb köbös lyukakat.

13. ábra. Egy kation mérete és a vegyület által elfoglalt lyuk alakja közvetlen kapcsolatban áll egymással.

Minden anionhoz két tetraéderes lyuk tartozik, akár HCP, akár CCP aniontömbben. Egy olyan vegyület, amely az anionok legszorosabban pakolt tömbjében kristályosodik, és a tetraéderes lyukakban kationok vannak, maximálisan 2:1 kation:anion arányú lehet; az összes tetraéderes lyuk ebben az arányban van kitöltve. Ilyen például a Li2O, a Na2O, a Li2S és a Na2S. A 2:1-nél kisebb arányú vegyületek is kristályosodhatnak a legszorosabban pakolt anionok és a tetraéderes lyukakban lévő kationok között, ha az ionméretek illeszkednek. Ezekben a vegyületekben azonban a tetraéderes lyukak egy része üresen marad.

A HCP vagy CCP szerkezetben az oktaéderes lyukak és az anionok aránya 1:1 arányú. Így az olyan vegyületek, amelyekben a kationok oktaéderes lyukakban vannak, az anionok legszorosabban pakolt tömbjében a kation:anion arány maximum 1:1 lehet. A NiO-ban, MnS-ben, NaCl-ban és KH-ban például az összes oktaéderes lyuk kitöltött. Az 1:1-nél kisebb arányok akkor figyelhetők meg, ha az oktaéderes lyukak egy része üresen marad.

Az anionok egyszerű kocka alakú tömbjében a tömb minden egyes anionjára jut egy kation által elfoglalható lyuk. A CsCl-ben és más hasonló szerkezetű vegyületekben az összes köbös lyuk foglalt. A SrH2, UO2, SrCl2 és CaF2 esetében a köbös lyukak fele foglalt.

A különböző típusú ionos vegyületek gyakran azonos szerkezetben kristályosodnak, ha ionjaik relatív mérete és sztöchiometriája (a szerkezetet meghatározó két fő jellemző) hasonló.

Ionvegyületek egységcellái

Nagyon sok ionvegyület kristályosodik köbös egységcellákkal, és ezeket a vegyületeket fogjuk használni az ionos szerkezetek általános jellemzőinek leírására.

Ha egy ionvegyület hasonló méretű kationokból és anionokból áll 1:1 arányban, akkor jellemzően egyszerű köbös szerkezetet alkot. Erre példa a cézium-klorid, CsCl (a 14. ábrán látható), amelynek Cs+ és Cl- sugara 174 pm, illetve 181 pm. Ezt úgy is elképzelhetjük, hogy a kloridionok egy egyszerű köbös egységcellát alkotnak, amelynek közepén egy céziumion van; vagy úgy, hogy a céziumionok egy egységcellát alkotnak egy kloridionnal a közepén; vagy úgy, hogy a Cs+ ionok által alkotott egyszerű köbös egységcellák átfedik a Cl-ionok által alkotott egységcellákat. A céziumionok és a kloridionok az egységcellák testátlói mentén érintkeznek. Egy egységcellánként egy céziumion és egy kloridion van jelen, ami a cézium-klorid képlete által megkövetelt l:l sztöchiometriát adja. Vegyük észre, hogy a cella közepén nincs rácspont, és a CsCl nem BCC szerkezet, mert a céziumion nem azonos a kloridionnal.

14. ábra. A hasonló méretű kationokkal és anionokkal rendelkező ionos vegyületek, mint például a CsCl, általában egyszerű kockaszerkezetet alkotnak. Ezek olyan egységcellákkal írhatók le, amelyeknek a sarkaiban vagy kationok, vagy anionok vannak.

Azt mondtuk, hogy a rácspontok elhelyezkedése tetszőleges. Ezt szemlélteti a CsCl szerkezet alternatív leírása, amelyben a rácspontok a céziumionok középpontjaiban helyezkednek el. Ebben a leírásban a céziumionok a cella sarkaiban lévő rácspontokon helyezkednek el, a kloridion pedig a cella közepén. A két egységcella eltérő, de azonos szerkezetet írnak le.

Ha egy ionos vegyület 1:1 arányban jelentősen eltérő méretű kationokból és anionokból áll, akkor jellemzően FCC egységcellával kristályosodik, mint amilyen a 15. ábrán látható. Erre példa a nátrium-klorid, NaCl, amelynek Na+ és Cl- sugarai 102 pm, illetve 181 pm. Ezt úgy képzelhetjük el, hogy a kloridionok egy FCC-cellát alkotnak, ahol a nátriumionok a cella széleinek közepén és a cella közepén lévő oktaéderes lyukakban helyezkednek el. A nátrium- és a kloridionok a cella szélei mentén érintkeznek egymással. Az egységcella négy nátriumiont és négy kloridiont tartalmaz, ami a NaCl képlethez szükséges 1:1 sztöchiometriát adja.

15. ábra. A kationoknál jóval nagyobb anionokkal rendelkező ionos vegyületek, mint például a NaCl, általában FCC-szerkezetet alkotnak. FCC-egységcellákkal írhatók le, amelyekben a kationok az oktaéderes lyukakban helyezkednek el.

A cink-szulfid köbös formája, a cinkblende szintén FCC-egységcellában kristályosodik, amint azt a 16. ábra szemlélteti. Ez a szerkezet szulfidionokat tartalmaz az FCC-rács rácspontjain. (A szulfidionok elrendeződése megegyezik a nátrium-kloridban lévő kloridionok elrendeződésével). Egy cinkion sugara csak körülbelül 40%-a egy szulfidion sugarának, így ezek a kis Zn2+ ionok váltakozó tetraéderes lyukakban helyezkednek el, vagyis a tetraéderes lyukak egyik felében. Az egységcellában négy cinkion és négy szulfidion található, így az empirikus képlet ZnS.

16. ábra. A ZnS, cink-szulfid (vagy cinkblende) egy FCC egységcellát alkot, ahol a szulfidionok a rácspontokon helyezkednek el, és a sokkal kisebb cinkionok a szerkezet tetraéderes lyukainak felét foglalják el.

A 17. ábrán láthatóhoz hasonló kalcium-fluorid egységcella szintén egy FCC egységcella, de ebben az esetben a kationok a rácspontokon helyezkednek el; az FCC-rács rácspontjain egyenértékű kalciumionok helyezkednek el. A kalciumionok FCC-táblázatában az összes tetraéderes helyet fluoridionok foglalják el. Egy egységcellában négy kalciumion és nyolc fluoridion található, ami a CaF2 kémiai képletben előírt l:2 kalcium:fluor arányt jelenti. A 17. ábra alapos vizsgálata a fluoridionok egyszerű köbös elrendezését mutatja, a köbös lyukak egyik felében kalciumionokkal. A szerkezet nem írható le a fluoridionok pontjainak térrácsával, mivel a fluoridionok nem mindegyike rendelkezik azonos környezettel. A négy kalciumion orientációja a fluoridionok körül eltérő.

17. ábra. A kalcium-fluorid, CaF2, egy FCC egységcellát alkot, amelyben a kalciumionok (zöld) a rácspontokban, a fluoridionok (piros) pedig a köztük lévő összes tetraéderes helyet elfoglalják.

Ion-sugarak számítása

Ha ismerjük egy ionos vegyület egységcellájának élhosszát és az ionok helyzetét a cellában, akkor kiszámíthatjuk a vegyületben lévő ionok ion-sugarát, ha feltételezéseket teszünk az egyes ionok alakjára és kontaktusaira vonatkozóan.

5. példa: Ionsugarak számítása

A LiCl (NaCl-szerű szerkezet, FCC) egységcellájának élhossza 0.514 nm vagy 5,14 Å. Feltételezve, hogy a lítiumion elég kicsi ahhoz, hogy a kloridionok érintkezzenek, mint a 15. ábrán, számítsuk ki a kloridion ionrádiuszát.

Megjegyzés: A hosszegység angström, Å, gyakran használják az atomi méretű méretek ábrázolására, és 10-10 m-nek felel meg.

Megoldás megjelenítése

A LiCl egységcella felületén a kloridionok a felület átlóján keresztül érintkeznek egymással:

Az egységcella felületén egy derékszögű háromszöget rajzolva láthatjuk, hogy az átló hossza négy kloridsugárral egyenlő (egy sugár minden sarokkloridtól és egy átmérő – ami két sugárral egyenlő – az oldal közepén lévő kloridiontól), tehát d = 4r. A Pitagorasz-tételből adódik:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}

amiből adódik:

\left(0.514\text{ nm}\right)^{2}+\left(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) Cl- sugár

Check Your Learning

A KCl (NaCl-szerű szerkezet, FCC) egységcellájának élhossza 6,28 Å. Feltételezve anion-kation kontaktust a cella éle mentén, számítsuk ki a káliumion sugarát. A kloridion sugara 1,82 Å.

Megoldás megjelenítése

A káliumion sugara 1,33 Å.

Fontos felismerni, hogy az egységcellák élhosszából számított ionsugarak értékei számos feltételezéstől függnek, például az ionok tökéletes gömb alakjától, amelyek a legjobb esetben is csak közelítések. Ennélfogva az ilyen számított értékek maguk is közelítő jellegűek, és az összehasonlításokat nem lehet túlságosan erőltetni. Mindazonáltal ez a módszer hasznosnak bizonyult az ionrádiuszok kiszámításához kísérleti mérésekből, például röntgenkrisztallográfiai meghatározásokból.

Röntgenkrisztallográfia

Az egységcella mérete és az atomok elrendeződése egy kristályban meghatározható a röntgensugarak kristály általi diffrakciójának méréseiből, amit röntgenkrisztallográfiának nevezünk. A diffrakció az elektromágneses hullám által tapasztalt terjedési irányváltozás, amikor az olyan fizikai akadályba ütközik, amelynek méretei a fény hullámhosszához hasonlóak. A röntgensugár elektromágneses sugárzás, amelynek hullámhossza körülbelül akkora, mint a kristályokban a szomszédos atomok közötti távolság (néhány Å nagyságrendű).

Amikor egy monokromatikus röntgensugárnyaláb becsapódik egy kristályba, a sugarakat a kristályban lévő atomok minden irányba szórják. Amikor az azonos irányban haladó szórt hullámok találkoznak egymással, interferencián mennek keresztül, amely folyamat során a hullámok egyesülnek, és az amplitúdó (intenzitás) növekedését vagy csökkenését eredményezik, attól függően, hogy az egyesülő hullámok maximumai milyen mértékben térnek el egymástól (lásd a 18. ábrát).

18. ábra. Az azonos teret elfoglaló fényhullámok interferenciát tapasztalnak, és egyesülve nagyobb (a) vagy kisebb (b) intenzitású hullámokat eredményeznek, attól függően, hogy a maximumok és a minimumok milyen távolságra vannak egymástól.

Ha egy bizonyos λ hullámhosszúságú röntgensugarakat a szomszédos kristálysíkokban lévő, d távolsággal elválasztott atomok szórnak, akkor konstruktív interferenciát tapasztalhatnak, ha a két hullám által az egyesülésük előtt megtett távolságok közötti különbség a hullámhossz n egész számú tényezője. Ez a feltétel akkor teljesül, ha a szórt sugár szöge, θ, a hullámhosszhoz és az atomok közötti távolsághoz a következő egyenlet szerint viszonyul:

n{\lambda }=2d\text{sin}\theta

Ezt az összefüggést Bragg-egyenletként ismerjük W. H. Bragg angol fizikus tiszteletére, aki először magyarázta meg ezt a jelenséget. A 19. ábra két példát mutat ugyanazon két kristálysíkból származó diffrakciós hullámokra. A bal oldali ábra a Bragg-szögben diffraktált hullámokat ábrázolja, ami konstruktív interferenciát eredményez, míg a jobb oldali ábra a diffrakciót és egy másik, a Bragg-feltételt nem teljesítő szöget mutatja, ami destruktív interferenciát eredményez.

Egy röntgendiffraktométer, mint például a 20. ábrán látható, használható a röntgensugarak diffrakciójának szögeinek mérésére, amikor a fent leírtak szerint kölcsönhatásba lépnek egy kristállyal. Az ilyen mérésekből a Bragg-egyenlet felhasználható az atomok közötti távolságok kiszámítására, amint azt a következő példafeladat bemutatja.

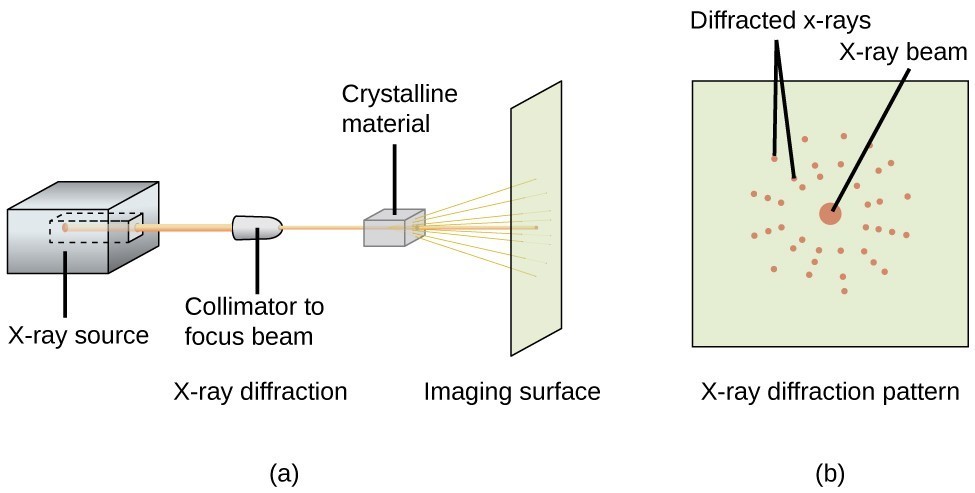
20. ábra. Egy diffraktométerben (a) a röntgensugárnyaláb egy kristályos anyagra esik, és egy röntgendiffrakciós mintázatot hoz létre (b), amelyet elemezve meghatározható a kristályszerkezet.

A “Celebrating Crystallography – An animated adventure” átiratát itt tekintheti meg (új ablakban nyílik meg).

Kémikus portréja: Röntgenkrisztallográfus Rosalind Franklin

21. ábra. Ez az illusztráció egy röntgendiffrakciós képet mutat, amely hasonló ahhoz, amit Franklin talált a kutatásai során. (hitel: National Institutes of Health)

A DNS szerkezetének felfedezése 1953-ban Francis Crick és James Watson által a tudomány történetének egyik legnagyobb eredménye. Ők kapták az 1962-es élettani vagy orvosi Nobel-díjat Maurice Wilkinsszel együtt, aki kísérleti úton bizonyította a DNS szerkezetét. Rosalind Franklin brit kémikus a DNS röntgendiffrakciós képének mérésében végzett munkájával felbecsülhetetlenül sokat tett hozzá ehhez a monumentális eredményhez. Pályafutása elején Franklin a szén szerkezetével kapcsolatos kutatásai hasznosnak bizonyultak a brit háborús erőfeszítések számára. Miután az 1950-es évek elején a biológiai rendszerekre helyezte át a hangsúlyt, Franklin és doktorandusz hallgatója, Raymond Gosling felfedezte, hogy a DNS két formából áll: egy hosszú, vékony szálból, amely nedves állapotban képződik (“B” típus), és egy rövid, széles szálból, amely szárításkor alakul ki (“A” típus). A DNS-ről készített röntgendiffrakciós felvételei (21. ábra) szolgáltatták azokat a döntő fontosságú információkat, amelyek lehetővé tették Watson és Crick számára, hogy megerősítsék, hogy a DNS kettős spirált alkot, és meghatározzák méretének és szerkezetének részleteit.

Franklin úttörő kutatásokat végzett a vírusokkal és a genetikai információikat tartalmazó RNS-szel kapcsolatban is, olyan új információkat tárva fel, amelyek gyökeresen megváltoztatták a terület ismeretanyagát. Miután petefészekrákot kapott, Franklin egészen 1958-ban, 37 évesen bekövetkezett haláláig dolgozott. Munkásságának számos posztumusz elismerése mellett a Finch Egészségtudományi Egyetem chicagói orvosi karának neve 2004-ben Rosalind Franklin Orvosi és Tudományegyetemre változott, és az egyetem hivatalos logójaként elfogadta a DNS-ről készült híres röntgendiffrakciós képét.

Glosszárium

testközpontú köbös (BCC) szilárdtest: olyan kristályos szerkezet, amelynek köbös egységcellája van, amelynek rácspontjai a cellasarkokban és a cella közepén vannak

testközpontú köbös egységcellában: A testközpontú köbös kristály legegyszerűbb ismétlődő egysége; ez egy kocka, amely minden sarkán és a kocka közepén rácspontokat tartalmaz

Bragg-egyenlet: egyenlet, amely összefüggésbe hozza azokat a szögeket, amelyekkel a röntgensugarak a kristályon belüli atomok által megtörnek

koordinációs szám: a kristályban egy adott atomhoz vagy egy komplexben a központi fématomhoz legközelebb eső atomok száma

kubikus legszorosabb pakolás (CCP): Olyan kristályszerkezet, amelyben szorosan pakolt atomok vagy ionok síkjai három, egymást váltó, különböző relatív orientációjú réteg sorozataként vannak egymásra helyezve (ABC)

diffrakció: Az elektromágneses sugárzás átirányítása, amely akkor következik be, amikor az megfelelő méretű fizikai akadályba ütközik

arcközpontú köbös (FCC) szilárdtest: kristályos szerkezet, amely egy köbös egységcellából áll, amelynek rácspontjai minden oldal sarkán és közepén vannak

arcközpontú köbös egységcella: Az arcközpontú köbös kristály legegyszerűbb ismétlődő egysége; ez egy kocka, amely minden sarkon és minden arc közepén rácspontokat tartalmaz

hexagonális legszorosabb pakolás (HCP): olyan kristályszerkezet, amelyben az atomok vagy ionok szorosan csomagolt rétegei két, egymást váltó, különböző relatív orientációjú (AB)

lyuk: (más néven: interstice) tér az atomok között egy kristályon belül

izomorf: azonos kristályszerkezettel rendelkező

oktaéderes lyuk: nyitott tér egy kristályban az oktaéder sarkaiban elhelyezkedő hat részecske középpontjában

egyszerű köbös egységcella: (más néven primitív köbös egységcella) egységcella az egyszerű köbös szerkezetben

egyszerű köbös szerkezet: olyan kristályszerkezet, amelynek köbös egységcellájában csak a sarkokban vannak rácspontok

térrács: egy kristályon belül minden olyan pont, amelynek azonos a környezete

tetraéderes lyuk: négy atom vagy ion által alkotott tetraéderes tér egy kristályban

egységcella: a térrács legkisebb része, amely három dimenzióban megismétlődik a teljes rácsot alkotva

röntgenkrisztallográfia: kísérleti technika a kristályban lévő atomok közötti távolságok meghatározására a röntgensugarak kristályon való áthaladásakor fellépő megtörési szögek mérésével

.