Mire jók a karaktertáblázatok?
Ez a pont egy jó kérdés: mi értelme van a karaktertáblázatokról tanulni? Az egyszerű válasz az, hogy egy molekula szimmetriája és a hozzá tartozó karaktertáblázat felhasználható a kémiailag jelentős spektroszkópiák, valamint a kötések számos aspektusának értelmezésére és előrejelzésére. Ezt a következőkben egy molekula rezgésmódjaira összpontosítva szemléltetjük.
A laboratóriumban infravörös (IR) és Raman-spektroszkópiával gyűjthetünk hasznos kísérleti adatokat. Ezeket az adatokat összehasonlíthatjuk a csoportelmélet és a helyes karaktertáblázat alkalmazásával megjósolt IR és/vagy Raman aktív sávok számával. A kezelés mögött álló matematika (csoportelmélet és mátrixalgebra) szilárd elméleti alapként szolgál. Az alább leírt manipulációk azért működnek, mert egy molekula összes szimmetriaművelete egy matematikai csoportot alkot, és engedelmeskedik a csoport szabályainak. Mint korábban megjegyeztük, nem kell elsajátítanunk a matematikának ezt a területét ahhoz, hogy jól használhassuk a karaktertáblákat.
Szabadságfokok és rezgések a molekulákban
Itt először egy egyszerű molekula (víz) szabadságfokait tárgyaljuk. Nagyon gyorsan látni fogjuk, hogy miért nagyon hasznos a szimmetria alkalmazása, amikor nagyobb molekulákat vizsgálunk.
Egy “N” atomot tartalmazó molekula esetében 3N szabadsági fok van (ne feledjük, hogy az x, y, z koordináták 3 dimenziós világában élünk). Egy nemlineáris molekula esetében 3 szabadságfokot lehet transzlációra – a test egészének mozgására (Tx, Ty, Tz) és 3 szabadságfokot rotációra (Rx, Ry, Rz) felírni. Az atomok többi mozgása az atomok elmozdulása az átlagos helyzetükből – a súlypont nem változik. Ezeket az alaprezgéseket “normálmódusoknak” nevezzük. Így egy nemlineáris molekulának 3N-6 normálmódusa van. A víz esetében a normálmódusok száma 3 (3 x 3 – 6 = 3). Lineáris molekulák esetében 3N-5 normálmódus van.
Víz esetében, amelyet természetesen intenzíven tanulmányoztak, tudjuk, hogy a 3 rezgés a következő:
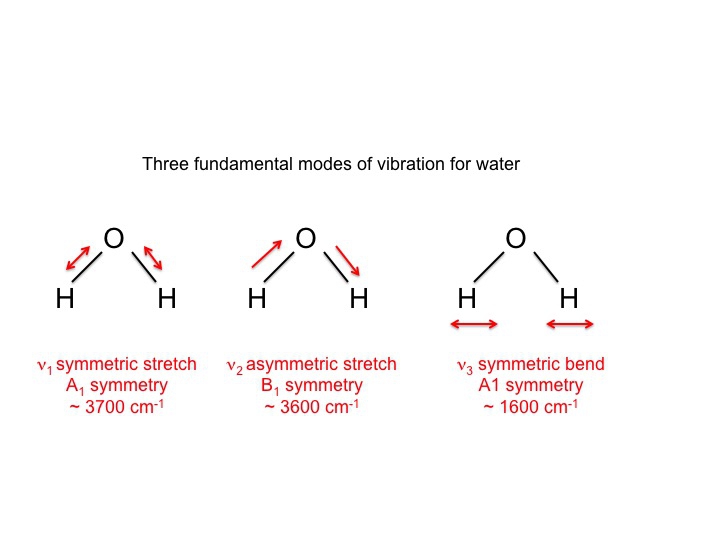
Az e módusok leírására használt szimbólumok (A1, B1) ugyanazok a Mulliken-szimbólumok, amelyekkel a karaktertáblák tárgyalásakor találkoztunk. Más szóval a rezgések, amelyek molekuláris tulajdonságok, szimmetriafajokkal vagy irreducibilis ábrázolásokkal írhatók le. Valójában a rezgésspektroszkópiával foglalkozó irodalom nagy része ezeket a szimbólumokat használja az információ közlésének rövidített módjaként.
Elég nyilvánvalónak kell lennie, hogy a rezgések száma gyorsan növekszik a molekulában lévő atomok számának még szerény növekedésével is. A rezgések fajtáinak meghatározása szemrevételezéssel (ahogyan azt a víz esetében tettük) most már sokkal nehezebbé válik. Vegyük például a következő vegyületeket:
H2O 3 atom 3 rezgés
PH3 4 atom 6 rezgés
CO22- 4 atom 6 rezgés
XeF4 5 atom 9 rezgés
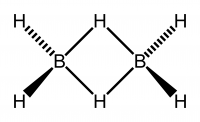
B2H6 8 atom 18 rezgés
A D2h szimmetriájú diborán (B2H6) esetében mind a 18 rezgés természetének és szimmetriafajának kitalálása szemrevételezéssel ijesztő feladat lenne. A D2h karaktertáblázatával és a szimmetriatulajdonságok ismeretével felfegyverkezve azonban az összes rezgés szimmetriafajának meghatározása egyszerű feladat.
Víz esetében a karaktertáblázatot (C2v) a molekuláris tulajdonságok oszlopában felsorolt 3 rezgéssel (ν1, v2, v3) tudnánk bemutatni az alábbiakban látható módon. (ν = görög szimbólum “nu”)

Általában azonban ez a megközelítés nem praktikus. Vegyük például a piridint (C5H5N). A pontcsoport szintén C2v, de a molekula 11 atomból áll. Az alaprezgésmódok száma 27 ( 3 x 11 – 6 = 27).
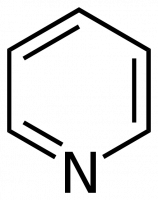
Ebben az esetben egy C2v karaktertáblázatot kellene készítenünk, amely mind a 27 rezgés szimmetriáját megmutatja. Emiatt a rezgések általában nem szerepelnek a karaktertáblázatokban. Ehelyett a felhasználóra (Önre) van bízva, hogy meghatározza a rezgések számát és típusát (a szimmetriafajták által meghatározottak szerint) minden olyan molekula esetében, amellyel találkozik. Hogy ezt hogyan tesszük, azt az alábbiakban ismertetjük.
Redukálható ábrázolások
Amint korábban említettük, a karaktertáblák egyik fontos tulajdonsága, hogy a szimmetriaműveletek egy matematikai csoport tagjai, és fontos kapcsolatok állnak fenn közöttük. Általában ugyanez mondható el a molekuláris tulajdonságok szimmetriafajtáiról vagy irreducibilis reprezentációiról is. Az irreducibilis reprezentációk karaktereinek akár szorzással, akár összeadással/kivonással történő kombinálásából származó termékek szintén a csoport szabályainak engedelmeskednek. Az új ábrázolások már nem a lehető legegyszerűbbek, és “redukálható ábrázolásoknak” nevezzük őket, mert alkotóelemeikre “redukálhatók”.
A víz esetében például a transzlációk (Tx, Ty, Tz) szimmetriái közvetlenül a C2v karaktertáblázatból nyerhetők ki. Ezek a következők: A1, B1 és B2. Mindhárom szabadságfokot ábrázolhatjuk egy ΓT ábrázolással, és felírhatjuk az alábbi kifejezést. (Γ = nagybetűs görög “gamma”).
ΓT = A1 + B1 + B2
Tudjuk, hogy A1, B1 és B2 csupán a szimmetriafajták (irreducibilis reprezentációk) rövidített jelölései. Ezért a ΓT karaktereit egyszerűen felírhatjuk úgy, hogy a C2v karaktertáblából összeadjuk az A1, B1 és B2 egyes karaktereit.
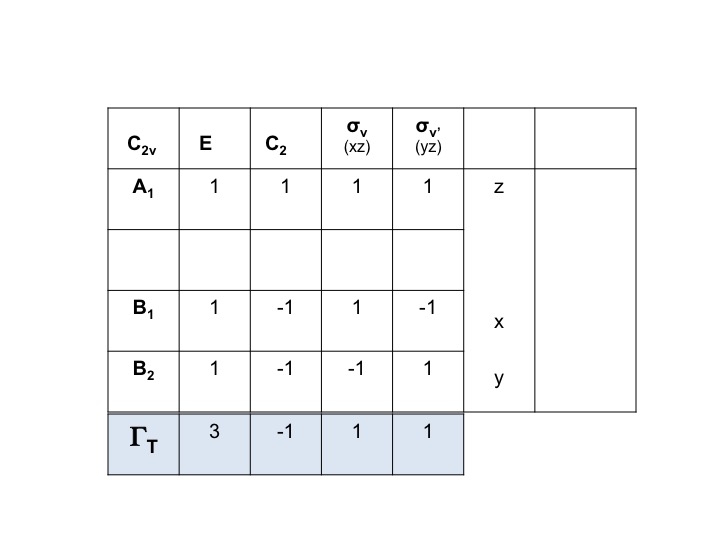
Így ΓT = 3 -1 1 1.
Ez egy érvényes redukálható ábrázolás és a C2v csoport tagja.
Hasonlóképpen felírhatjuk mindhárom forgás és az összes rezgés redukálható ábrázolását.
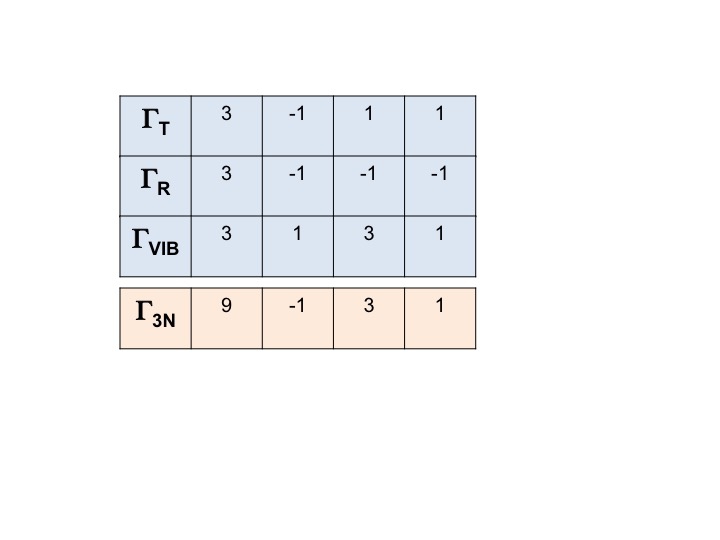
A molekula (3N) MINDEN szabadsági fokára vonatkozó reprezentáció felírható így:
Γ3N = ΓT + ΓR + ΓVIB
és a redukálható reprezentációját úgy kapjuk meg, hogy egyszerűen összeadjuk a ΓT, ΓR és ΓVIB karaktereket.
Γ3N = 9 -1 3 1
Jegyezzük fel ezt – később még szóba fog kerülni!
Bár a 9 -1 3 1 karakterhalmaz a C2v csoport érvényes tagja, a molekuláris tulajdonságok tárgyalásakor nem különösebben hasznos. Amire igazán szükség van, az a rövidített szimmetriafajták nyelve (Mulliken-szimbólumok, A1, B1 stb.). Más szóval a Γ3N-t az A1, B1 stb. kifejezésekkel akarjuk kifejezni. A fentiekben tárgyalt információkból szemrevételezéssel könnyen kimutatható, hogy:
Γ3N = 3A1 +A2 + 3B1 +2B2
A jó hír, hogy más, bonyolultabb molekulák esetében ezt a feladatot nem kell szemrevételezéssel elvégeznünk, mert:
1. Könnyen előállíthatjuk a Γ3N redukálható ábrázolását egy molekulának (ha ismerjük a pontcsoport-szimmetriáját).
2. A Γ3N redukálható ábrázolását könnyen átalakíthatjuk a szimmetriafajták (Mulliken-szimbólumok) összegévé egy “egyszerű” képlet, az úgynevezett redukciós képlet segítségével.
Általános módszer a Γ3N előállítására
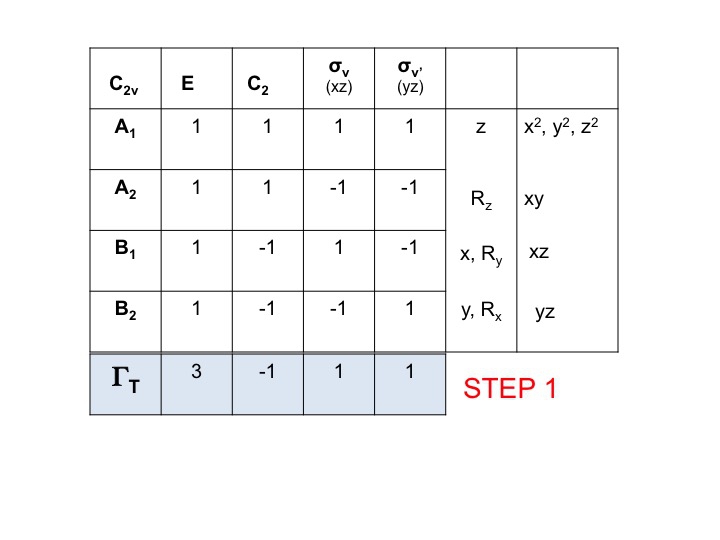
1. lépés
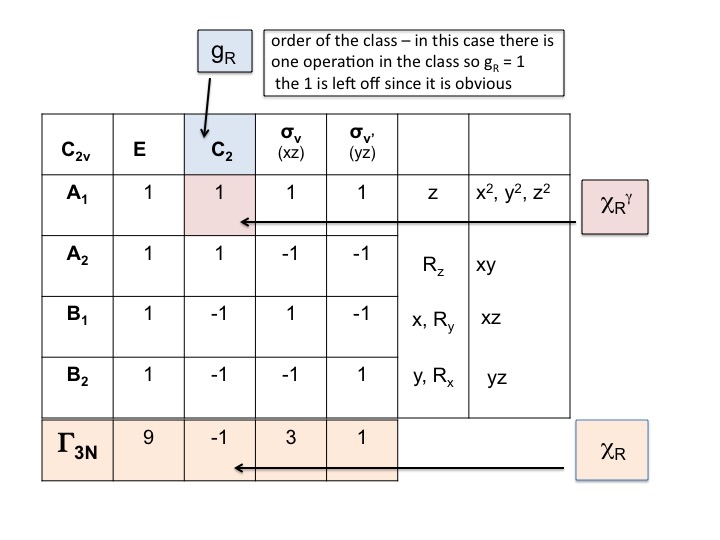
Vegyük a molekula karaktertáblázatát, és adjunk hozzá egy sort az alján. Ebben a sorban hozzuk létre a ΓT (vagy Γxyz) redukálható ábrázolását, ahogy fentebb tettük, egyszerűen az egyes műveletekhez tartozó karakterek hozzáadásával, amelyek megfelelnek az x, y és z molekula tulajdonságainak. A C2v esetében már megmutattuk, hogy ezek az A1-nek, B1-nek és B2-nek megfelelő karakterek.
2. lépés
Tegyünk még egy sort a ΓT alá, és írjuk fel azoknak az atomoknak a számát, amelyek NEM VÁLTOZNAK a helyükön az egyes szimmetriaoperációk során. Itt jön rá, hogy mennyire hasznos egy valódi molekulamodellkészlet. Ehhez az is szükséges, hogy tudd, hol vannak a szimmetriaelemek, és hogyan hatnak a szimmetriaműveletek a molekulára. Természetesen már tudod, hogyan kell ezt megtenni, mert tanultad a Schönflies jelölést, és tudod, hogyan kell hozzárendelni egy molekula pontcsoportját. A karaktertáblázatban a felső sor mentén az összes szimmetriaművelet is osztályonként van felsorolva.
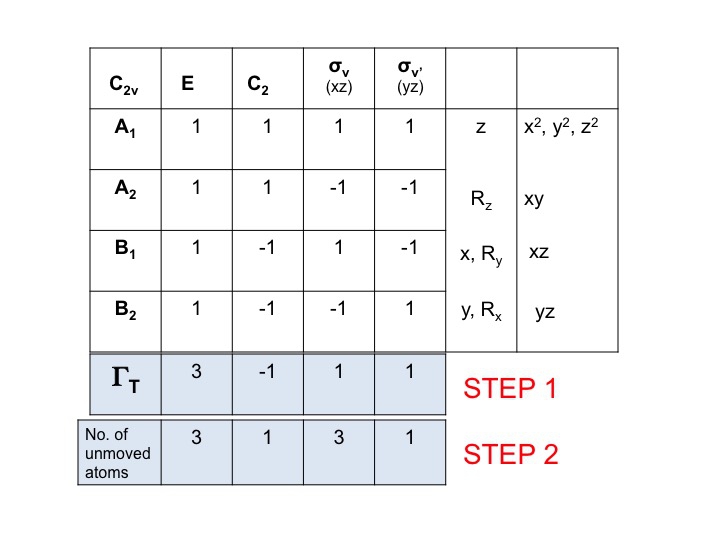
Így a víz esetében (3 atom) az E alatt 3 mozdulatlan atom van, a C2 esetében viszont mindkét H mozog, de mivel az O atom a C2 tengelyen ül, nem változtatja meg a helyét, ezért a C2 oszlop alatt 1-et írunk be. A 2. lépésben előállított új számhalmaz (3 1 3 1) szintén redukálható ábrázolás a C2v-ben, és engedelmeskedik a csoport szabályainak.
3. lépés
Ebben a lépésben egyszerűen összeszorozzuk az 1. és 2. lépésben előállított karaktereket. Az eredmény (harmadik sor) a Γ3N (vagy ΓTOT) redukálható ábrázolása. Ilyen egyszerű.
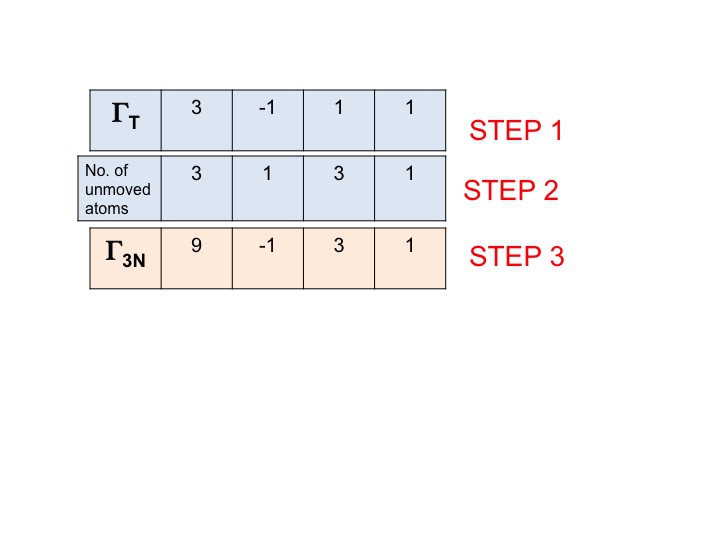
Megfigyelhetjük, hogy az új redukálható ábrázolás (9 -1 1 3) megegyezik a Γ3N ábrázolásával, amelyet korábban szemrevételezéssel kaptunk.
Redukálható reprezentáció redukálása
Hogy MINDEN redukálható reprezentációt redukálhatatlan reprezentációinak (szimmetriafajták vagy Mulliken-szimbólumok) összegévé alakítsunk át, egy redukciós képletet használunk:

Ezt az információt könnyen megtalálhatjuk a karaktertáblázatban:
Visszatérve a vízre vonatkozó példánkhoz: C2v pontcsoport, rend (g) = 4
A redukálható ábrázolás a Γ3N = 9 -1 3 1
Az A1-nek ebben az ábrázolásban való előfordulásának száma tehát
aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3
tehát Γ3N 3 A1 szimmetriájú fajt tartalmaz. A többi szimmetriafaj számát a következőképpen számoljuk ki:
aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 egy A2 van jelen
aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 B1 jelen
aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1.1} = 2 2 B2 jelen
Most felírhatjuk Γ3N = 3A1 + A2 + 3B1 + 2B2 (pontosan azt, amit a fenti “ellenőrzéssel” kaptunk. Most már kivonhatjuk a transzlációk és rotációk szimmetriafajtáit, és így megkapjuk az alaprezgésmódok számát és szimmetriafajtáit. A ΓT és ΓR értékeket közvetlenül a karaktertáblázatból kaphatjuk meg.
Γ3N = 3A1 + A2 + 3B1 + 2B2
ΓT = A1 + B1 + B2
ΓR = A2 + B1 + B2
ΓVIB = Γ3N – ΓT – ΓR = 2A1 +B1
A víz három normálrezgésmódja tehát A1 szimmetriájú, A1 és B1.
Most már rendelkezünk egy általános módszerrel egy molekula összes alaprezgésmódjának meghatározására, és e módusok kifejezésére a Mulliken-szimbólumok rövidített nyelvén. Ez az egyik olyan feladat, amelyből az 1. vizsgán vizsgázni fog. A legjobb módja annak, hogy magabiztossá válj ebben a módszerben, ha minél több lehetséges példát gyakorolsz!”
Következő: Válogatási szabályok