Az entitások közötti fontosságot, hatalmat vagy befolyást vizsgáló tudósok egyik növekvő érdeklődési területe az úgynevezett gráfelmélet. A gráfelmélet gyökerei 1736-ban kezdődtek, amikor Carl Ehler matematikus bemutatta Leonhard Eulernek a Königsberg hídjai problémát.

A Königsberg hídjai probléma alapja az egykori német város, Königsberg, amely a Pregel folyó két oldalán fekszik. Középen két nagy sziget volt, amelyeket hét híd kötött össze egymással és a folyóparttal. Carl Ehler megszállottja lett annak, hogy olyan útvonalat találjon, amelyen keresztül mind a hét hídon át lehet menni anélkül, hogy bármelyiken is többször átsétálna. Ehler felkereste Leonhard Eulert, egy svájci matematikust. Euler megerősítette Ehler hipotézisét, miszerint a problémának nincs megoldása, és Euler magyarázata egy új matematikai paradigma, a Helyzetgeometria alapjául szolgált.

Euler új geometriai paradigmája azt állította, hogy a hidak elhelyezkedése nem számít. A probléma ehelyett egyszerűsíthető, ha minden hidat ponttá (csomóponttá) alakítunk, a köztük lévő kapcsolatokat pedig vonalak (élek) jelképezik. A csomópontok és élek használatának ezt a gyakorlatát ma már gráfelméletként ismerjük.

A királyhegyi hidak problémájáról itt olvashat bővebben.

A gráfelmélet kezdetben nem sok célt szolgált a problémamegoldásban, és a matematikusok nem tartották nagyra. A nagy permutációk feldolgozására alkalmas modern számítási teljesítmény azonban gyakorlatiasabbá tette a gráfelmélet elveit. Ez a cikk megtanítja a Gráfelmélet elveinek alkalmazását Python-alapú elemzésekben.

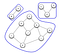
Nem minden hálózat egy Gráf rendszerben összekapcsolódik. Ez az összekapcsolatlanság az, amikor komponensek alakulnak ki. Ahogy az alábbi gráf mutatja, csak akkor alakul ki komponens, ha minden csomópontnak van útja más csomópontokhoz.

Alkalmazott gráfelmélet Pythonban

A Pythonban a networkx-et gyakran használják alkalmazott gráfelméletre, más néven hálózatelemzésre . A csomag hasznos funkciókkal rendelkezik egy gráf jellemzőinek gyors összegzésére. Átnézheti az alábbi lépéseket, és követheti, ahogy létrehozunk egy gráfot, és megértjük a felépítését.

Az alábbi kód először létrehoz egy P üres gráf objektumot. A következő lépések csomópontokat adnak hozzá, és leírják az éleket.

Az olyan eszközök, mint a <object>.nodes() vagy a <object>.edges() gyors lehetőséget nyújtanak a gráfrendszer összes csomópontjának és élének megtekintésére.

print(P.nodes())print(P.edges())

Végül a nx.draw a hálózat megjelenítésére szolgál.

%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)

GYakorlatok 1:

Most, hogy a gráfok alapfogalmait megbeszéltük, a következő feladatok jó módszer a gyakorlásra:

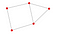
• Hány csomópont van a fenti gráfban?
• Hány él van a fenti gráfban?
• Melyik az E és C geodézia?
• Egynél több komponens van a gráfban?

Valós adatok felhasználása

Az alábbi feladat az Egyesült Államokon belüli 2015-ös járatok adatait használja. Az adatkészlet tartalmazza a kiindulási és célrepülőtereket, valamint a járatot leíró attribútumokat, beleértve a repülési időt és a késéseket (időjárási, biztonsági vagy légitársasággal kapcsolatos).

Mivel az adatkészlet nagy, a gyakorlat a Los Angeles környéki repülőterekről (Los Angeles (LAX), Burbank (BUR), Orange County (SNA) és San Bernardino County (ONT)) induló járatokra koncentrál. Ezenkívül a hangsúly az olyan járatok áttekintésén lesz, amelyek hasonlítanak az én Deloitte utazási ütemtervemhez – vasárnap repülök ki és csütörtökön jövök vissza.

Mivel már rendelkezünk kiindulási és célállomás adatokkal, a ****fields ORIGIN_AIRPORT és DESTINATION_AIRPORT a csomópontok és élek forrásmezőiként szolgálnak – nincs szükség csomópontok és élek létrehozására, ahogy azt az első gyakorlatban tettük. Miután a csomópontok definiálva vannak, a <object>.edges() biztosítja a köztük lévő összes páronkénti kapcsolatot. Végül a nx.draw segít létrehozni egy gráfot az élekhez.

FG.edges()

nx.draw(FG, with_labels = True)

A fenti kimenet, a csomópontok repülőtéri kódokkal vannak jelölve. Minden él a négy Los Angeles környéki repülőtér valamelyikére vezet, mivel csak ezt a négyet választottuk ki ehhez a feladathoz. A Los Angeles International (LAX) a legnagyobb repülőtér a négy közül, és a grafikonon jól látható, hogy sok város csak az LAX-ről érhető el, más kisebb repülőterekről nem. Ez jól mutatja az LAX összekapcsoltságát, vagyis fokozati centralitását. A networkx-ben nx.algorithms.degree_centrality(<object>) ****a gráfrendszerben az egyes csomópontok centralitásának megtalálására használjuk.

# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)

Mehetünk szemléletesebbek is, és egy rövid “for loop” segítségével éleket állíthatunk elő két érdekes terület között. Például a következő kódot arra használjuk, hogy megtaláljuk az összes lehetséges járatot San Bernardino megyéből (ONT) Newarkba (EWR) vasárnap vagy csütörtökön.

A San Bernardino megye és Newark közötti számos járatlehetőség közül a nx.dijkstra_path segítségével megtalálhatjuk az euklideszi utat (vagy a legrövidebb utat).

#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path

gyakorlatok 2:

• A nx.draw() segítségével állítsuk elő a következő gráfot. Megjegyzés: a hálózatod nem biztos, hogy pontosan ugyanúgy néz ki, de az utaknak, éleknek és csomópontoknak meg kell egyezniük az alábbi hálózatéval.
• Nyomtasd ki az összes élt.
• Melyik a legrövidebb út L-ből F-be?