Moins…
![]()
![]()
Un triplet pythagoricien est un triplet d’entiers positifs ![]() ,
, ![]() , et
, et ![]() tel qu’il existe un triangle rectangle avec des branches
tel qu’il existe un triangle rectangle avec des branches ![]() et une hypoténuse
et une hypoténuse ![]() . Par le théorème de Pythagore, cela revient à trouver des entiers positifs
. Par le théorème de Pythagore, cela revient à trouver des entiers positifs ![]() ,
, ![]() , et
, et ![]() satisfaisant
satisfaisant
|
(1)
|
Le plus petit et le plus connu des triplés pythagoriciens est ![]() . Le triangle rectangle ayant ces longueurs de côté est parfois appelé le triangle 3, 4, 5.
. Le triangle rectangle ayant ces longueurs de côté est parfois appelé le triangle 3, 4, 5.
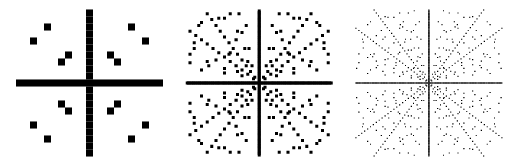
Les tracés des points dans le plan ![]() tels que
tels que ![]() est un triple de Pythagore sont montrés ci-dessus pour des bornes successivement plus grandes. Ces tracés incluent les valeurs négatives de
est un triple de Pythagore sont montrés ci-dessus pour des bornes successivement plus grandes. Ces tracés incluent les valeurs négatives de ![]() et
et ![]() , et sont donc symétriques par rapport aux axes x et y.
, et sont donc symétriques par rapport aux axes x et y.

De même, les tracés des points dans le plan ![]() tels que
tels que ![]() est un triplet pythagoricien sont montrés ci-dessus pour des bornes successivement plus grandes.
est un triplet pythagoricien sont montrés ci-dessus pour des bornes successivement plus grandes.

Il est habituel de ne considérer que les triplets pythagoriciens primitifs (appelés aussi triplets « réduits ») dans lesquels ![]() et
et ![]() sont relativement premiers, puisque d’autres solutions peuvent être générées trivialement à partir des primitifs. Les triples primitifs sont illustrés ci-dessus, et on peut voir immédiatement que les lignes radiales correspondant aux triples imprimitifs dans le tracé original sont absentes dans cette figure. Pour les solutions primitives, l’un des
sont relativement premiers, puisque d’autres solutions peuvent être générées trivialement à partir des primitifs. Les triples primitifs sont illustrés ci-dessus, et on peut voir immédiatement que les lignes radiales correspondant aux triples imprimitifs dans le tracé original sont absentes dans cette figure. Pour les solutions primitives, l’un des ![]() ou
ou ![]() doit être pair, et l’autre impair (Shanks 1993, p. 141),
doit être pair, et l’autre impair (Shanks 1993, p. 141), ![]() étant toujours impair.
étant toujours impair.
En outre, un côté de chaque triple pythagoricien est divisible par 3, un autre par 4, et un autre par 5. Un côté peut avoir deux de ces diviseurs, comme dans (8, 15, 17), (7, 24, 25), et (20, 21, 29), ou même les trois, comme dans (11, 60, 61).
Donné un triplet primitif ![]() , trois nouveaux triplets primitifs sont obtenus à partir de
, trois nouveaux triplets primitifs sont obtenus à partir de
|
(2)
|
|||
|
(3)
|
|||
|
(4)
|
où
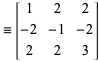 |
(5)
|
|
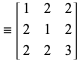 |
(6)
|
|
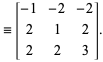 |
(7)
|
Hall (1970) et Roberts (1977) prouvent que ![]() est un triple primitif pythagoricien si
est un triple primitif pythagoricien si
|
(8)
|
où ![]() est un produit fini des matrices
est un produit fini des matrices ![]() ,
, ![]() ,
, ![]() . Il s’ensuit donc que tout triple primitif pythagoricien doit être un membre du tableau infini
. Il s’ensuit donc que tout triple primitif pythagoricien doit être un membre du tableau infini
 |
(9)
|
Pythagore et les Babyloniens ont donné une formule pour générer des triples (pas nécessairement primitifs) comme
|
(10)
|
pour ![]() , ce qui génère un ensemble de triplets distincts ne contenant ni tous les triplets primitifs ni tous les triplets imprimitifs (et où dans le cas particulier
, ce qui génère un ensemble de triplets distincts ne contenant ni tous les triplets primitifs ni tous les triplets imprimitifs (et où dans le cas particulier ![]() ,
, ![]() ).
).
Les Grecs anciens donnaient
|
(11)
|
où ![]() et
et ![]() sont relativement premiers et de parité opposée (Shanks 1993, p. 141), ce qui génère un ensemble de triplets distincts contenant précisément les triplets primitifs (après avoir trié de manière appropriée
sont relativement premiers et de parité opposée (Shanks 1993, p. 141), ce qui génère un ensemble de triplets distincts contenant précisément les triplets primitifs (après avoir trié de manière appropriée ![]() et
et ![]() ).
).
Laissez ![]() être un nombre de Fibonacci. Alors
être un nombre de Fibonacci. Alors
|
(12)
|
génère des triples de Pythagore distincts (Dujella 1995), bien que de manière non exhaustive pour les triples primitifs ou imprimitifs. Plus généralement, en partant des entiers positifs ![]() ,
, ![]() , et en construisant la suite de type Fibonacci
, et en construisant la suite de type Fibonacci ![]() avec les termes
avec les termes ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , …. génère des triplets pythagoriciens distincts
, …. génère des triplets pythagoriciens distincts
|
(13)
|
(Horadam 1961), où
|
(24)
|
(Beiler 1966, p. 116). Notez que ![]() si
si ![]() est premier ou deux fois premier. Les premiers nombres pour
est premier ou deux fois premier. Les premiers nombres pour ![]() , 2, … sont 0, 0, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 4, 1, …. (OEIS A046079).
, 2, … sont 0, 0, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 4, 1, …. (OEIS A046079).
Pour trouver le nombre de façons ![]() dont un nombre
dont un nombre ![]() peut être l’hypoténuse d’un triangle rectangle primitif, écrire sa factorisation comme
peut être l’hypoténuse d’un triangle rectangle primitif, écrire sa factorisation comme
|
(25)
|
où les ![]() s sont de la forme
s sont de la forme ![]() et les
et les ![]() s sont de la forme
s sont de la forme ![]() . Le nombre de triangles droits primitifs possibles est alors
. Le nombre de triangles droits primitifs possibles est alors
|
(26)
|
Par exemple, ![]() puisque
puisque
|
(27)
|
|||
|
(28)
|
Les valeurs de ![]() pour
pour ![]() , 2, … sont 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, …. (OEIS A024362). Les quelques premiers nombres premiers de la forme
, 2, … sont 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, …. (OEIS A024362). Les quelques premiers nombres premiers de la forme ![]() sont 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, …. (OEIS A002144), donc les plus petites longueurs de côté qui sont les hypoténuses de 1, 2, 4, 8, 16, … triangles droits primitifs sont 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).
sont 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, …. (OEIS A002144), donc les plus petites longueurs de côté qui sont les hypoténuses de 1, 2, 4, 8, 16, … triangles droits primitifs sont 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).
Le nombre de triangles rectangles primitifs ou non primitifs possibles ayant ![]() comme hypoténuse est
comme hypoténuse est
|
(29)
|
|||
|
(30)
|
(correction de la coquille de Beiler 1966, p. 117, qui indique que cette formule ne donne que le nombre de solutions non primitives), où ![]() est la fonction somme des carrés. Par exemple, il existe quatre triangles entiers distincts dont l’hypoténuse est 65, puisque
est la fonction somme des carrés. Par exemple, il existe quatre triangles entiers distincts dont l’hypoténuse est 65, puisque
|
(31)
|
Les premiers nombres pour ![]() , 2, … sont 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, …. (OEIS A046080). Les plus petits hypoténus ayant
, 2, … sont 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, …. (OEIS A046080). Les plus petits hypoténus ayant ![]() triples distincts sont 1, 5, 25, 125, 65, 3125, …. (OEIS A006339). Le tableau suivant donne les hypoténuses pour lesquelles il existe exactement
triples distincts sont 1, 5, 25, 125, 65, 3125, …. (OEIS A006339). Le tableau suivant donne les hypoténuses pour lesquelles il existe exactement ![]() triangles entiers droits distincts pour
triangles entiers droits distincts pour ![]() , 1, …, 5.
, 1, …, 5.
| OEIS | hypoténuses pour lesquelles il existe |
|
| 0 | A004144 | 1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, …. |
| 1 | A084645 | 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, … |
| 2 | A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, ….. |
| 3 | A084647 | 125, 250, 375, 500, 750, 875, 1000, 1125, 1375, … |
| 4 | A084648 | 65, 85, 130, 145, 170, 185, 195, 205, 221, 255, …. |
| 5 | A084649 | 3125, 6250, 9375, 12500, 18750, 21875, 25000, … |
Donc, le nombre total de façons dont ![]() peut être soit un pied soit une hypoténuse d’un triangle rectangle est donné par
peut être soit un pied soit une hypoténuse d’un triangle rectangle est donné par
|
(32)
|
Les valeurs de ![]() , 2, … sont 0, 0, 1, 1, 1, 2, 1, 1, 2, 2, 2, 1, 4, 2, 1, 5, 3, …. (OEIS A046081). Les plus petits nombres
, 2, … sont 0, 0, 1, 1, 1, 2, 1, 1, 2, 2, 2, 1, 4, 2, 1, 5, 3, …. (OEIS A046081). Les plus petits nombres ![]() qui peuvent être les côtés de
qui peuvent être les côtés de ![]() triangles droits généraux pour
triangles droits généraux pour ![]() , 2, … sont 3, 5, 16, 12, 15, 125, 24, 40, …. (OEIS A006593 ; Beiler 1966, p. 114).
, 2, … sont 3, 5, 16, 12, 15, 125, 24, 40, …. (OEIS A006593 ; Beiler 1966, p. 114).
Il existe 50 triplets pythagoriciens dont l’hypoténuse est inférieure à 100, dont les premiers, triés par ![]() croissants, sont (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084, et A009000).
croissants, sont (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084, et A009000).
Parmi ceux-ci, seuls 16 sont des triplets primitifs dont l’hypoténuse est inférieure à 100 : (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89), et (65, 72, 97) (OEIS A046086, A046087, et A020882).
Disons que le nombre de triplets avec hypoténuse ![]() est noté
est noté ![]() , le nombre de triplets avec hypoténuse
, le nombre de triplets avec hypoténuse ![]() est noté
est noté ![]() , et le nombre de triplets primitifs inférieurs à
, et le nombre de triplets primitifs inférieurs à ![]() est noté
est noté ![]() . Puis le tableau suivant résume les valeurs des puissances de 10.
. Puis le tableau suivant résume les valeurs des puissances de 10.
| OEIS | |
|
| A101929 | 1, 50, 878, 12467, … | |
| A101930 | 2, 52, 881, 12471, ….. | |
| A101931 | 1, 16, 158, 1593, … |
Lehmer (1900) a prouvé que le nombre de solutions primitives avec hypoténuse inférieure à ![]() satisfait
satisfait
|
(33)
|
(OEIS A086201).

Les inradii des quelques premiers triangles de Pythagore primitifs ordonnés par ![]() croissants sont donnés par 1, 2, 3, 3, 6, 5, 4, 10, 5, …. (OEIS A014498).
croissants sont donnés par 1, 2, 3, 3, 6, 5, 4, 10, 5, …. (OEIS A014498).
Il existe une méthode générale pour obtenir des triplets de triangles de Pythagore avec des aires égales. Prenez les trois ensembles de générateurs comme
|
(34)
|
|||
|
(35)
|
|||
|
(36)
|
|||
|
(37)
|
|||
|
(38)
|
|||
|
(39)
|
Alors le triangle rectangle engendré par chaque triple (![]() ) a une aire commune
) a une aire commune
|
(40)
|
(Beiler 1966, pp. 126-127). Le seul extremum de cette fonction se produit à ![]() . Puisque
. Puisque ![]() pour
pour ![]() , la plus petite aire partagée par trois triangles droits non primitifs est donnée par
, la plus petite aire partagée par trois triangles droits non primitifs est donnée par ![]() , ce qui donne une aire de 840 et correspond aux triplets (24, 70, 74), (40, 42, 58), et (15, 112, 113) (Beiler 1966, p. 126).
, ce qui donne une aire de 840 et correspond aux triplets (24, 70, 74), (40, 42, 58), et (15, 112, 113) (Beiler 1966, p. 126).
Les triangles droits dont les aires consistent en un seul chiffre comprennent ![]() (aire de 6) et
(aire de 6) et ![]() (aire de 666666 ; Wells 1986, p. 89).
(aire de 666666 ; Wells 1986, p. 89).
En 1643, Fermat a mis au défi Mersenne de trouver un triplet pythagoricien dont l’hypoténuse et la somme des jambes étaient des carrés. Fermat a trouvé la plus petite solution de ce type :
|
(41)
|
|||
|
(42)
|
|||
|
(43)
|
avec
|
(44)
|
|||
|
(45)
|
Un problème connexe consiste à déterminer si un entier spécifié ![]() peut être l’aire d’un triangle rectangle avec des côtés rationnels. 1, 2, 3 et 4 ne sont les aires d’aucun triangle rectangle à côtés rationnels, mais 5 est (3/2, 20/3, 41/6), tout comme 6 (3, 4, 5). La solution du problème implique la courbe elliptique
peut être l’aire d’un triangle rectangle avec des côtés rationnels. 1, 2, 3 et 4 ne sont les aires d’aucun triangle rectangle à côtés rationnels, mais 5 est (3/2, 20/3, 41/6), tout comme 6 (3, 4, 5). La solution du problème implique la courbe elliptique
|
(46)
|
Une solution (![]() ,
, ![]() ,
, ![]() ) existe si (46) a une solution rationnelle, auquel cas
) existe si (46) a une solution rationnelle, auquel cas
|
(47)
|
|||
|
(48)
|
(Koblitz 1993). Il n’existe pas de méthode générale connue pour déterminer s’il existe une solution pour des ![]() arbitraires, mais une technique conçue par J. Tunnell en 1983 permet d’écarter certaines valeurs (Cipra 1996).
arbitraires, mais une technique conçue par J. Tunnell en 1983 permet d’écarter certaines valeurs (Cipra 1996).
.