Un domaine d’intérêt croissant pour les scientifiques qui explorent l’importance, le pouvoir ou l’influence entre les entités est appelé la théorie des graphes. Les racines de la théorie des graphes ont commencé en 1736 lorsque le mathématicien Carl Ehler a présenté à Leonhard Euler le problème des ponts de Konigsberg.
Le problème des ponts de Konigsberg est basé sur l’ancienne ville allemande de Konigsberg qui s’étend sur les deux côtés de la rivière Pregel. Au centre, il y avait deux grandes îles qui étaient reliées l’une à l’autre et aux berges de la rivière par sept ponts. Carl Ehler est devenu obsédé par la recherche d’un itinéraire permettant de traverser chacun des sept ponts sans enjamber aucun plus d’une fois. Ehler a contacté Leonhard Euler, un mathématicien suisse. Euler a confirmé l’hypothèse d’Ehler selon laquelle le problème n’avait pas de solution, et l’explication d’Euler a informé un nouveau paradigme mathématique appelé géométrie de position.
Le nouveau paradigme de géométrie d’Euler a déclaré que l’emplacement des ponts n’avait pas d’importance. Le problème, au contraire, peut être simplifié en transformant chaque pont en un point (nœud) avec des lignes (arêtes) pour représenter les liens entre eux. Cette pratique de l’utilisation des nœuds et des arêtes est maintenant connue sous le nom de théorie des graphes.
Vous pouvez en savoir plus sur le problème des ponts de Konigsberg ici.
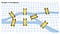
A l’origine, la théorie des graphes ne servait pas beaucoup à la résolution de problèmes et n’était pas très appréciée des mathématiciens. Cependant, la puissance de calcul moderne permettant de traiter de grandes permutations a rendu les principes de la théorie des graphes plus pratiques. Cet article vous apprend à appliquer les principes de la Théorie des graphes à l’analyse basée sur Python.


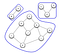
Les réseaux d’un système graphique ne sont pas tous interconnectés. Cette déconnexion est le moment où les composants sont formés. Comme le montre le graphique ci-dessous, une composante est formée uniquement lorsque chaque nœud a un chemin vers d’autres nœuds.
Théorie appliquée des graphes en Python
En Python, networkx est souvent utilisé pour la théorie appliquée des graphes également connue sous le nom d’analyse de réseau . Le paquet a des fonctionnalités utiles pour résumer rapidement les caractéristiques d’un graphe. Vous pouvez revoir les étapes ci-dessous et suivre la création d’un graphe et la compréhension de sa composition.
D’abord, le code ci-dessous crée un objet vide de graphe P. Les étapes suivantes ajoutent des nœuds et décrivent les arêtes.
Des arguments tels que <object>.nodes() ou <object>.edges() sont des moyens rapides de visualiser tous les nœuds et arêtes du système de graphe.
print(P.nodes())print(P.edges())
Enfin, nx.draw est utilisé pour visualiser le réseau.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
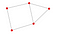
Exercices 1:
Maintenant que les concepts de base des graphes sont discutés, les exercices suivants sont une bonne méthode pour s’exercer:
- Combien de nœuds y a-t-il dans le graphe ci-dessus ?
- Combien d’arêtes y a-t-il dans le graphe ci-dessus ?
- Quel est le géodésique pour E et C ?
- Y a-t-il plus d’une composante dans le graphe ?
Utilisation de données réelles
L’exercice ci-dessous utilisera des données pour les vols à l’intérieur des États-Unis en 2015. L’ensemble de données comprend les aéroports d’origine et de destination en plus des attributs qui décrivent le vol, notamment le temps de vol et les retards (liés à la météo, à la sécurité ou à la compagnie aérienne).
Parce que l’ensemble de données est important, l’exercice se concentrera sur les vols en provenance des aéroports de la région de Los Angeles (Los Angeles (LAX), Burbank (BUR), Orange County (SNA) et San Bernardino County (ONT)). En outre, l’accent sera mis sur l’examen des vols qui ressemblent à mon horaire de voyage chez Deloitte, soit un départ le dimanche et un retour le jeudi.
Puisque nous avons déjà des données d’origine et de destination, ****fields ORIGIN_AIRPORT et DESTINATION_AIRPORT serviront de champs sources pour les nœuds et les arêtes – il n’est pas nécessaire de créer des nœuds ou des arêtes comme nous l’avons fait dans le premier exercice. Une fois les nœuds définis, <object>.edges() fournira toutes les relations par paires entre eux. Enfin, nx.draw aidera à produire un graphique aux bords.

FG.edges()

nx.draw(FG, with_labels = True)

Dans la sortie ci-dessus, les noeuds sont étiquetés avec les codes des aéroports. Toutes les arêtes mènent à l’un des quatre aéroports de la région de Los Angeles, car ces quatre aéroports ont été les seuls sélectionnés pour cet exercice. Los Angeles International (LAX) est le plus grand aéroport parmi les quatre et le graphique montre clairement que de nombreuses villes ne sont accessibles que par LAX et non par d’autres aéroports plus petits. Cela met en évidence la connectivité, ou la centralité de degré, de LAX. Dans networkx, nx.algorithms.degree_centrality(<object>) ****est utilisé pour trouver la centralité de chaque nœud dans le système de graphe.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
Nous pouvons aller plus granulairement et utiliser une courte ‘boucle for’ pour produire des arêtes entre deux zones d’intérêt. Par exemple, le code suivant est utilisé pour trouver tous les vols possibles entre le comté de San Bernardino (ONT) et Newark (EWR) le dimanche ou le jeudi.
Parmi les plusieurs options de vol entre le comté de San Bernardino et Newark, le nx.dijkstra_path peut être utilisé pour trouver le chemin euclidien (ou le chemin le plus court).
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
Exercices 2:
- Produisez le graphe suivant en utilisant
nx.draw(). Note : votre réseau peut ne pas avoir exactement la même apparence mais les chemins, les arêtes et les nœuds doivent correspondre au réseau ci-dessous. - Imprimez toutes les arêtes.
- Quel est le chemin le plus court de L à F ?

.