Objectifs d’apprentissage
À la fin de cette section, vous serez en mesure de :
- Identifier les relations mathématiques entre les diverses propriétés des gaz
- Utiliser la loi combinée des gaz, et les lois des gaz connexes, pour calculer les valeurs de diverses propriétés des gaz dans des conditions spécifiées
Au cours du dix-septième et surtout du dix-huitième siècle, poussés à la fois par le désir de comprendre la nature et par la quête de la fabrication de ballons dans lesquels ils pourraient voler (figure 1), un certain nombre de scientifiques ont établi les relations entre les propriétés physiques macroscopiques des gaz, à savoir la pression, le volume, la température et la quantité de gaz. Bien que leurs mesures ne soient pas précises selon les normes actuelles, ils ont pu déterminer les relations mathématiques entre les paires de ces variables (par exemple, pression et température, pression et volume) qui sont valables pour un gaz idéal – une construction hypothétique que les gaz réels approchent dans certaines conditions. Finalement, ces lois individuelles ont été combinées en une seule équation – la loi des gaz idéaux – qui relie les quantités de gaz pour les gaz et est assez précise pour les basses pressions et les températures modérées. Nous allons considérer les développements clés des relations individuelles (pour des raisons pédagogiques, pas tout à fait dans l’ordre historique), puis les rassembler dans la loi des gaz idéaux.

Figure 1. En 1783, le premier (a) vol en ballon rempli d’hydrogène, (b) vol en ballon à air chaud habité, et (c) vol en ballon rempli d’hydrogène habité ont eu lieu. Lors de l’atterrissage du ballon à hydrogène représenté en (a), les villageois de Gonesse, effrayés, l’auraient détruit avec des fourches et des couteaux. Le lancement de ce dernier aurait été vu par 400 000 personnes à Paris.
Pression et température : Loi de Gay-Lussac
Imaginez que vous remplissez de gaz un récipient rigide fixé à un manomètre, puis que vous fermez le récipient de façon à ce qu’aucun gaz ne puisse s’échapper. Si le récipient est refroidi, le gaz à l’intérieur devient également plus froid et on observe que sa pression diminue. Comme le récipient est rigide et hermétiquement fermé, le volume et le nombre de moles de gaz restent constants. Si on chauffe la sphère, le gaz à l’intérieur devient plus chaud (figure 2) et la pression augmente.

Figure 2. L’effet de la température sur la pression du gaz : Lorsque la plaque chauffante est éteinte, la pression du gaz dans la sphère est relativement faible. Lorsque le gaz est chauffé, la pression du gaz dans la sphère augmente.
Cette relation entre la température et la pression est observée pour tout échantillon de gaz confiné dans un volume constant. Un exemple de données expérimentales de pression-température est présenté pour un échantillon d’air dans ces conditions à la figure 3. On constate que la température et la pression sont liées linéairement, et si la température est sur l’échelle kelvin, alors P et T sont directement proportionnels (encore une fois, lorsque le volume et les moles de gaz sont maintenus constants) ; si la température sur l’échelle kelvin augmente d’un certain facteur, la pression du gaz augmente du même facteur.
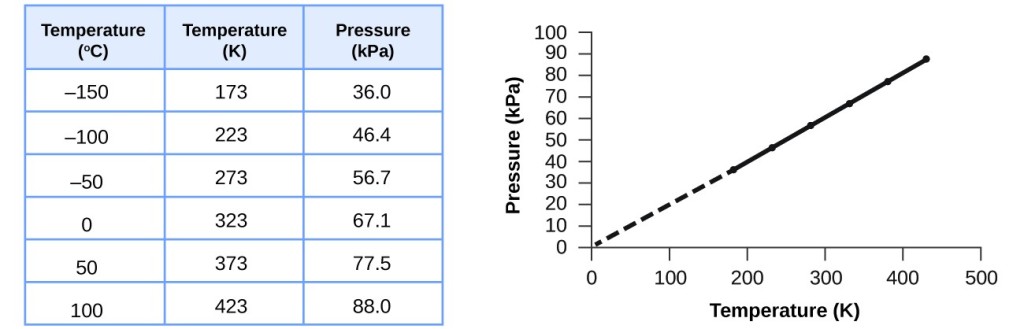
Figure 3. Pour un volume et une quantité d’air constants, la pression et la température sont directement proportionnelles, à condition que la température soit en kelvin. (Les mesures ne peuvent pas être faites à des températures plus basses à cause de la condensation du gaz). Lorsque cette droite est extrapolée à des pressions plus basses, elle atteint une pression de 0 à -273 °C, soit 0 sur l’échelle des kelvins et la température la plus basse possible, appelée zéro absolu.
Guillaume Amontons a été le premier à établir empiriquement la relation entre la pression et la température d’un gaz (~1700), et Joseph Louis Gay-Lussac a déterminé cette relation de façon plus précise (~1800). De ce fait, la relation P-T pour les gaz est connue sous le nom de loi de Gay-Lussac ou de loi d’Amontons. Sous l’une ou l’autre de ces appellations, elle indique que la pression d’une quantité donnée de gaz est directement proportionnelle à sa température sur l’échelle des kelvins lorsque le volume est maintenu constant. Mathématiquement, cela peut s’écrire :
\large P\propto T
\large P=\text{constant}\times T
\large P=k\times T
où ∝ signifie « est proportionnel à », et k est une constante de proportionnalité qui dépend de l’identité, de la quantité et du volume du gaz.
\large\frac{{P}_{1}}{{T}}_{1}}=\frac{{P}_{2}}{{T}_{2}}
Cette équation est utile pour les calculs de pression-température pour un gaz confiné à volume constant. Notez que les températures doivent être sur l’échelle kelvin pour tout calcul de la loi des gaz (0 sur l’échelle kelvin et la température la plus basse possible est appelée zéro absolu). (Notez également qu’il existe au moins trois façons de décrire l’évolution de la pression d’un gaz en fonction de sa température : Nous pouvons utiliser un tableau de valeurs, un graphique ou une équation mathématique.)
Volume et température : Loi de Charles
Si nous remplissons un ballon d’air et que nous le scellons, le ballon contient une quantité spécifique d’air à la pression atmosphérique, disons 1 atm. Si nous mettons le ballon dans un réfrigérateur, le gaz à l’intérieur se refroidit et le ballon rétrécit (bien que la quantité de gaz et sa pression restent constantes). Si nous rendons le ballon très froid, il se rétrécit beaucoup, et il se dilate à nouveau lorsqu’il se réchauffe.
Cette vidéo montre comment le refroidissement et le chauffage d’un gaz entraînent respectivement une diminution ou une augmentation de son volume.
Ces exemples de l’effet de la température sur le volume d’une quantité donnée d’un gaz confiné à pression constante sont vrais en général : Le volume augmente lorsque la température augmente, et diminue lorsque la température diminue. Les données de volume-température pour un échantillon de 1 mole de gaz méthane à 1 atm sont énumérées et représentées graphiquement dans la figure 4.

Figure 4. Le volume et la température sont linéairement liés pour 1 mole de gaz méthane à une pression constante de 1 atm. Si la température est en kelvin, le volume et la température sont directement proportionnels. La ligne s’arrête à 111 K car le méthane se liquéfie à cette température ; lorsqu’on l’extrapole, elle coupe l’origine du graphique, représentant une température de zéro absolu.
La relation entre le volume et la température d’une quantité donnée de gaz à pression constante est connue sous le nom de loi de Charles en reconnaissance du scientifique français et pionnier du vol en ballon Jacques Alexandre César Charles. La loi de Charles stipule que le volume d’une quantité donnée de gaz est directement proportionnel à sa température sur l’échelle des kelvins lorsque la pression est maintenue constante.
Mathématiquement, cela peut s’écrire ainsi :
\large V\propto T
\large V=\text{constant}\cdot T
\large V=k\cdot T
avec k étant une constante de proportionnalité qui dépend de la quantité et de la pression du gaz.
\large\frac{{V}_{1}}{T}_{1}}=\frac{{V}_{2}}{{T}_{2}}
Volume et pression : loi de Boyle
Si nous remplissons partiellement une seringue hermétique avec de l’air, la seringue contient une quantité spécifique d’air à température constante, disons 25 °C. Si nous enfonçons lentement le piston tout en maintenant la température constante, le gaz contenu dans la seringue est comprimé dans un plus petit volume et sa pression augmente ; si nous retirons le piston, le volume augmente et la pression diminue. Cet exemple de l’effet du volume sur la pression d’une quantité donnée d’un gaz confiné est vrai en général. Diminuer le volume d’un gaz confiné augmentera sa pression, et augmenter son volume diminuera sa pression. En fait, si le volume augmente d’un certain facteur, la pression diminue du même facteur, et vice versa. Les données de volume et de pression d’un échantillon d’air à température ambiante sont représentées graphiquement sur la figure 5.

Figure 5. Lorsqu’un gaz occupe un plus petit volume, il exerce une pression plus élevée ; lorsqu’il occupe un plus grand volume, il exerce une pression plus faible (en supposant que la quantité de gaz et la température ne changent pas). Comme P et V sont inversement proportionnels, un graphique de 1/P en fonction de V est linéaire.
Contrairement aux relations P-T et V-T, la pression et le volume ne sont pas directement proportionnels l’un à l’autre. Au lieu de cela, P et V présentent une proportionnalité inverse : L’augmentation de la pression entraîne une diminution du volume du gaz. Mathématiquement, cela peut s’écrire :
\large P\propto 1\text{/}V\text{ ou }P=k\cdot 1\text{/}V\text{ ou }P\cdot V=k\text{ ou }{P}_{1}{V}_{1}={P}_{2}{V}_{2}
avec k étant une constante. Graphiquement, cette relation est illustrée par la ligne droite qui résulte du tracé de l’inverse de la pression \large\left(\frac{1}{P}\right) en fonction du volume (V), ou de l’inverse du volume \large\left(\frac{1}{V}\right) en fonction de la pression (V). Les graphiques avec des lignes courbes sont difficiles à lire avec précision pour les valeurs faibles ou élevées des variables, et ils sont plus difficiles à utiliser pour adapter les équations et les paramètres théoriques aux données expérimentales. Pour ces raisons, les scientifiques essaient souvent de trouver un moyen de « linéariser » leurs données. Si nous traçons P en fonction de V, nous obtenons une hyperbole (voir figure 6).
La relation entre le volume et la pression d’une quantité donnée de gaz à température constante a été publiée pour la première fois par le philosophe naturel anglais Robert Boyle il y a plus de 300 ans. Elle est résumée dans l’énoncé connu aujourd’hui sous le nom de loi de Boyle : Le volume d’une quantité donnée de gaz maintenu à température constante est inversement proportionnel à la pression sous laquelle il est mesuré.
La chimie en action : La respiration et la loi de Boyle
Que faites-vous environ 20 fois par minute pendant toute votre vie, sans interruption, et souvent sans même en avoir conscience ? La réponse, bien sûr, est la respiration, ou la respiration. Comment cela fonctionne-t-il ? Il s’avère que les lois des gaz s’appliquent ici. Vos poumons absorbent le gaz dont votre corps a besoin (l’oxygène) et se débarrassent des déchets gazeux (le dioxyde de carbone). Les poumons sont constitués d’un tissu spongieux et extensible qui se dilate et se contracte lorsque vous respirez. Lorsque vous inspirez, votre diaphragme et vos muscles intercostaux (les muscles situés entre vos côtes) se contractent, ce qui élargit votre cavité thoracique et augmente le volume de vos poumons. L’augmentation du volume entraîne une diminution de la pression (loi de Boyle). L’air s’écoule alors dans les poumons (de la haute pression vers la basse pression). Lorsque vous expirez, le processus s’inverse : Les muscles de votre diaphragme et de vos côtes se détendent, votre cage thoracique se contracte et le volume de vos poumons diminue, ce qui entraîne une augmentation de la pression (loi de Boyle à nouveau), et l’air s’échappe des poumons (de la haute pression à la basse pression). Vous inspirez et expirez ensuite, encore et encore, répétant ce cycle de la loi de Boyle pour le reste de votre vie (figure 7).
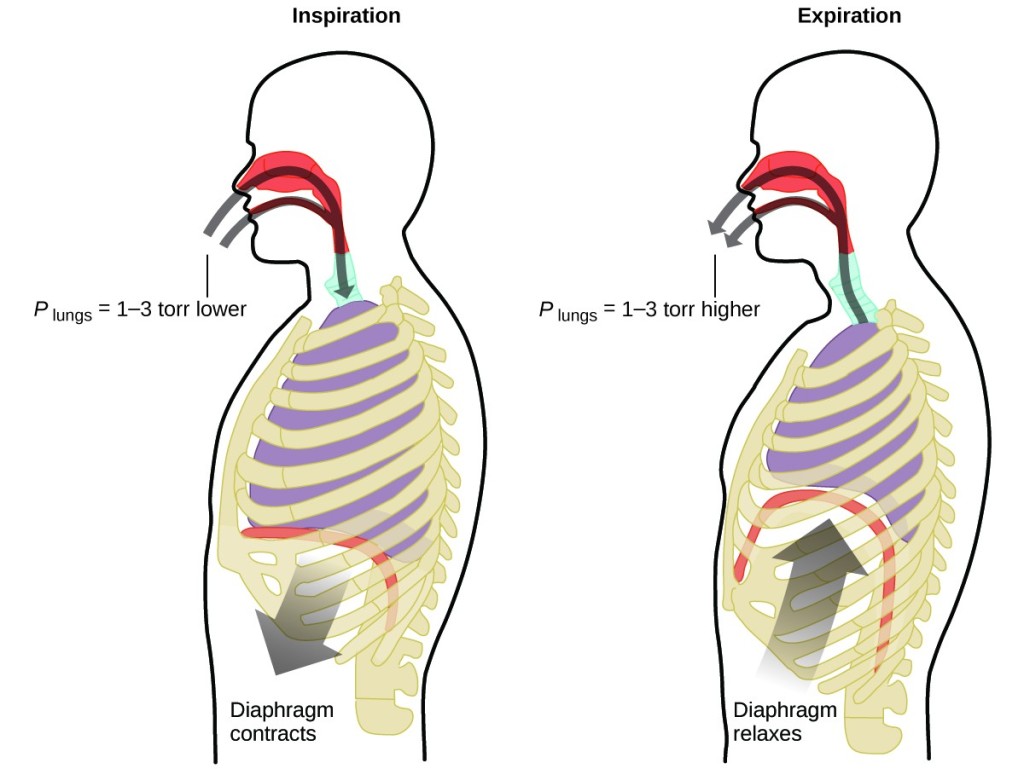
Figure 7. La respiration se produit parce que l’expansion et la contraction du volume des poumons créent de petites différences de pression entre vos poumons et votre environnement, provoquant l’aspiration et l’expulsion de l’air de vos poumons.
Moles de gaz et volume : Loi d’Avogadro
Le scientifique italien Amedeo Avogadro a avancé une hypothèse en 1811 pour rendre compte du comportement des gaz, affirmant que des volumes égaux de tous les gaz, mesurés dans les mêmes conditions de température et de pression, contiennent le même nombre de molécules. Au fil du temps, cette relation a été confirmée par de nombreuses observations expérimentales et exprimée par la loi d’Avogadro : Pour un gaz confiné, le volume (V) et le nombre de moles (n) sont directement proportionnels si la pression et la température restent toutes deux constantes.
Sous forme d’équation, cela s’écrit comme suit :
\large\begin{array}{ccccc}V\propto n& \text{or}& V=k\times n& \text{or}& \frac{{V}_{1}}{{n}_{1}}=\frac{{V}_{2}}{{n}_{2}}\end{array}
Des relations mathématiques peuvent également être déterminées pour les autres paires de variables, comme P par rapport à n, et n par rapport à T.
Glossaire
zéro absolu : température à laquelle le volume d’un gaz serait nul selon la loi de Charles.
La loi d’Avogadro : le volume d’un gaz à température et pression constantes est proportionnel au nombre de molécules de gaz
La loi de Boyle : le volume d’un nombre donné de moles de gaz maintenu à température constante est inversement proportionnel à la pression sous laquelle il est mesuré
La loi de Charles : le volume d’un nombre donné de moles de gaz est directement proportionnel à sa température kelvin lorsque la pression est maintenue constante
La loi de Gay-Lussac : (également, loi d’Amontons) la pression d’un nombre donné de moles de gaz est directement proportionnelle à sa température kelvine lorsque le volume est maintenu constant
.