Chimie pour les majeures

août 5, 2021
| Aucun commentaire

Résultats d’apprentissage

  • Décrire l’arrangement des atomes et des ions dans les structures cristallines
  • Calculer les rayons ioniques en utilisant les dimensions des cellules unitaires
  • Expliquer l’utilisation des mesures de diffraction des rayons X pour déterminer les structures cristallines

Plus de 90% des solides naturels et artificiels sont cristallins.pour déterminer les structures cristallines

Plus de 90% des solides naturels et artificiels sont cristallins. La plupart des solides se forment avec un arrangement régulier de leurs particules car les interactions attractives globales entre les particules sont maximisées, et l’énergie intermoléculaire totale est minimisée, lorsque les particules s’entassent de la manière la plus efficace. L’arrangement régulier au niveau atomique se reflète souvent au niveau macroscopique. Dans ce module, nous allons explorer certains détails sur les structures des solides cristallins métalliques et ioniques, et apprendre comment ces structures sont déterminées expérimentalement.

Les structures des métaux

Nous commencerons notre discussion sur les solides cristallins en considérant les métaux élémentaires, qui sont relativement simples parce que chacun ne contient qu’un seul type d’atome. Un métal pur est un solide cristallin dont les atomes métalliques sont serrés les uns contre les autres selon un motif répétitif. Certaines des propriétés des métaux en général, telles que leur malléabilité et leur ductilité, sont en grande partie dues à la présence d’atomes identiques disposés selon un schéma régulier. Les différentes propriétés d’un métal par rapport à un autre dépendent en partie de la taille de leurs atomes et des spécificités de leur disposition spatiale. Nous allons explorer les similitudes et les différences de quatre des géométries cristallines métalliques les plus courantes dans les sections qui suivent.

Cellules unitaires des métaux

La structure d’un solide cristallin, qu’il s’agisse d’un métal ou non, est mieux décrite en considérant son unité répétitive la plus simple, que l’on appelle sa cellule unitaire. La cellule unitaire est constituée de points du réseau qui représentent les emplacements des atomes ou des ions. La structure entière consiste alors en cette cellule unitaire se répétant en trois dimensions, comme l’illustre la figure 1.

Deux dessins sont donnés. A gauche, un cube est rendu avec des points de réseau à chaque coin, et des cellules unitaires comme côtés. A droite, le même cube est représenté répliqué en caractères grisés, pour montrer un réseau infini de cubes similaires.

Figure 1. Une cellule unitaire montre les emplacements des points du réseau qui se répètent dans toutes les directions.

Débutons notre étude de la structure du réseau cristallin et des cellules unitaires par la structure la plus simple et la cellule unitaire la plus basique. Pour visualiser cela, imaginez que vous prenez un grand nombre de sphères identiques, comme des balles de tennis, et que vous les disposez uniformément dans un récipient. La façon la plus simple de procéder consiste à former des couches dans lesquelles les sphères d’une couche sont directement au-dessus de celles de la couche inférieure, comme l’illustre la figure 2. Cet arrangement est appelé structure cubique simple, et la cellule unitaire est appelée cellule unitaire cubique simple ou cellule unitaire cubique primitive.

Trois dessins du même cube de 10,44. A gauche, des cercles sont dessinés autour des points de treillis. Au milieu, ces cercles de points de treillis deviennent des sphères brunes imposées à la boîte. A droite, on voit le même rendu des boîtes infinies que dans 10.44.

Figure 2. Lorsque les atomes métalliques sont disposés avec des sphères dans une couche directement au-dessus ou au-dessous des sphères dans une autre couche, la structure du réseau est appelée cubique simple. Notez que les sphères sont en contact.

Dans une structure cubique simple, les sphères ne sont pas emballées aussi étroitement qu’elles pourraient l’être, et elles ne « remplissent » qu’environ 52% du volume du récipient. C’est un arrangement relativement inefficace, et seul un métal (le polonium, Po) cristallise dans une structure cubique simple. Comme le montre la figure 3, un solide présentant ce type d’agencement est constitué de plans (ou couches) dans lesquels chaque atome n’entre en contact qu’avec les quatre voisins les plus proches de sa couche, un atome directement au-dessus de lui dans la couche supérieure et un atome directement au-dessous de lui dans la couche inférieure. Le nombre d’autres particules avec lesquelles chaque particule d’un solide cristallin est en contact est appelé le nombre de coordination. Pour un atome de polonium dans un réseau cubique simple, le nombre de coordination est donc de six.

Deux dessins sont présentés. A gauche, la pile infinie de cubes de 10.44 apparaît, cette fois-ci uniquement en noir et blanc. L'accent est mis sur un point du treillis et les lignes qui lui sont immédiatement adjacentes sur les bords des cubes. A droite, le même dessin apparaît, cette fois avec le point de réseau en rouge, et les lignes rayonnantes qui en partent étiquetées 1-6.

Figure 3. Un atome dans une structure de réseau cubique simple est en contact avec six autres atomes, il a donc un nombre de coordination de six.

Dans un réseau cubique simple, la cellule unitaire qui se répète dans toutes les directions est un cube défini par les centres de huit atomes, comme le montre la figure 4. Les atomes des coins adjacents de cette cellule unitaire sont en contact les uns avec les autres, de sorte que la longueur de l’arête de cette cellule est égale à deux rayons atomiques, ou à un diamètre atomique. Une cellule unitaire cubique ne contient que les parties de ces atomes qui s’y trouvent. Étant donné qu’un atome situé à un coin d’une cellule unitaire cubique simple est contenu par un total de huit cellules unitaires, seul un huitième de cet atome se trouve dans une cellule unitaire spécifique. Et puisque chaque cellule unitaire cubique simple possède un atome à chacun de ses huit « coins », il y a 8 \times \frac{1}{8}=1 atome à l’intérieur d’une cellule unitaire cubique simple.

Deux dessins sont présentés. À gauche, l

Figure 4. Une cellule unitaire de réseau cubique simple contient un huitième d’atome à chacun de ses huit coins, elle contient donc un atome au total.

Exemple 1 : Calcul du rayon atomique et de la densité pour les métaux, partie 1

La longueur d’arête de la cellule unitaire du polonium alpha est de 336 pm.

  1. Déterminez le rayon d’un atome de polonium.
  2. Déterminez la densité du polonium alpha.
Afficher la solution

Le polonium alpha cristallise dans une cellule unitaire cubique simple:

Un diagramme montre un cube avec une portion d'un huitième de huit sphères à l'intérieur du cube, une section dans chaque coin. Le long du côté inférieur droit du cube se trouvent deux flèches à double extrémité qui s'étirent chacune le long de la moitié de la distance totale à travers le cube. Chaque flèche est étiquetée
  1. Deux atomes de Po adjacents se contactent, donc la longueur du bord de cette cellule est égale à deux rayons atomiques de Po : l=2r. Par conséquent, le rayon de Po est r=\dfrac{\text{l}{2}=\dfrac{\text{336 pm}{2}=\text{168 pm}.
  2. La densité est donnée par \text{densité}=\text{masse}{\text{volume}}. La densité du polonium peut être trouvée en déterminant la densité de sa cellule unitaire (la masse contenue dans une cellule unitaire divisée par le volume de la cellule unitaire). Comme une cellule unitaire de Po contient un huitième d’un atome de Po à chacun de ses huit coins, une cellule unitaire contient un atome de Po.

La masse d’une cellule unitaire de Po peut être trouvée par :

\text{1 cellule unitaire de Po}\times \dfrac{\text{1 atome de Po}{\text{1 cellule unitaire de Po}\times \dfrac{\text{1 mol de Po}}{6.022\times {10}^{23}\text{Po atoms}\times \dfrac{208.998\text{g}{\text{1 mol Po}}=3.47\times {10}^{-22}\text{g}

Le volume d’une cellule unitaire de Po peut être trouvé par:

V={l}^{3}={(336\times {10}^{-10}\text{cm})}^{3}=3.79\times {10}^{-23}{\text{cm}}^{3}

(Notez que la longueur du bord a été convertie de pm en cm pour obtenir les unités de volume habituelles pour la densité.)

Donc, la densité de \text{Po}=\dfrac{3.471\times {10}^{-22}\text{g}{3,79\times {10}^{-23}{\text{cm}}^{3}}={\text{9,16 g/cm}}^{3}

Check Your Learning

La longueur de l’arête de la cellule unitaire du nickel est de 0,3524 nm. La densité du Ni est de 8,90 g/cm3. Le nickel cristallise-t-il dans une structure cubique simple ? Expliquez.

Montrer la solution

Non. Si le Ni était cubique simple, sa densité serait donnée par:

\text{1 atome de Ni}\times \dfrac{\text{1 mol Ni}}{6.022\times {10}^{23}\text{Ni atoms}\times \dfrac{58.693\text{g}{\text{1 mol Ni}}=9.746\times {10}^{-23}\text{g}
V={l}^{3}={(3.524\times {10}^{-8}\text{cm})}^{3}=4.376\times {10}^{-23}{\text{cm}}^{3}

Alors la densité du Ni serait =\dfrac{9.746\times {10}^{-23}\text{g}}{4.376\times {10}^{-23}{\text{cm}}^{3}={\text{2.23 g/cm}}^{3}

Puisque la densité réelle du Ni n’est pas proche de celle-ci, le Ni ne forme pas une structure cubique simple.

La plupart des cristaux métalliques constituent l’un des quatre grands types de cellules unitaires. Pour l’instant, nous nous concentrerons sur les trois cellules unitaires cubiques : cubique simple (que nous avons déjà vu), cellule unitaire cubique centrée sur le corps et cellule unitaire cubique centrée sur la face – toutes illustrées à la figure 5. (Notez qu’il existe en fait sept systèmes de treillis différents, dont certains ont plus d’un type de treillis, pour un total de 14 types différents de cellules unitaires. Nous laissons les géométries plus compliquées pour plus tard dans ce module.)

La première rangée de dessins est étiquetée "emplacements des points de treillis". En dessous, il y a trois images. À gauche, le cube unitaire simple avec 6 points de treillis. Au milieu se trouve un cube unitaire légèrement plus grand avec un point rouge au milieu. À droite, une unité cubique encore plus grande avec 6 points rouges à l

Figure 5. Les cellules unitaires cubiques des métaux montrent (dans les figures supérieures) les emplacements des points du réseau et (dans les figures inférieures) les atomes de métal situés dans la cellule unitaire.

Certains métaux cristallisent dans un arrangement qui a une cellule unitaire cubique avec des atomes à tous les coins et un atome au centre, comme le montre la figure 6. C’est ce qu’on appelle un solide cubique centré sur le corps (BCC). Les atomes des coins d’une cellule unitaire BCC ne sont pas en contact les uns avec les autres mais avec l’atome du centre. Une cellule unitaire BCC contient deux atomes : un huitième d’un atome à chacun des huit coins ( 8\times \frac{1}{8}=1 atome des coins) plus un atome du centre. Tout atome de cette structure touche quatre atomes de la couche qui le précède et quatre atomes de la couche qui le suit. Ainsi, un atome dans une structure BCC a un nombre de coordination de huit.

Trois dessins apparaissent. À gauche, le même dessin d'une unité cubique avec un point rouge au centre, de la figure 10.48. Au milieu, c'est le même cube avec des molécules grises superposées, avec une molécule rouge au centre, comme la rangée du bas de la figure 10.48. A gauche, nous voyons les parties des molécules à l'extérieur du cube rasées, et seuls des morceaux des molécules grises et la molécule rouge entière restant.

Figure 6. Dans une structure cubique centrée sur le corps, les atomes d’une couche spécifique ne se touchent pas. Chaque atome touche quatre atomes dans la couche au-dessus de lui et quatre atomes dans la couche en dessous.

Les atomes dans les arrangements BCC sont emballés beaucoup plus efficacement que dans une structure cubique simple, occupant environ 68% du volume total. Les métaux isomorphes ayant une structure BCC comprennent K, Ba, Cr, Mo, W et Fe à température ambiante. (On dit que les éléments ou les composés qui cristallisent avec la même structure sont isomorphes.)

De nombreux autres métaux, comme l’aluminium, le cuivre et le plomb, cristallisent selon un arrangement qui présente une cellule unitaire cubique avec des atomes à tous les coins et au centre de chaque face, comme l’illustre la figure 7. Cet arrangement est appelé un solide cubique à faces centrées (FCC). Une cellule unitaire FCC contient quatre atomes : un huitième d’un atome à chacun des huit coins (8 fois \frac{1}{8}=1 atome des coins) et un demi-atome sur chacune des six faces (6 fois \frac{1}{2}=3 atomes des faces). Les atomes des coins touchent les atomes des centres des faces adjacentes le long des diagonales des faces du cube. Comme les atomes sont sur des points de réseau identiques, ils ont des environnements identiques.

Trois dessins apparaissent. À gauche, on voit la même unité cubique avec 6 points rouges à l'intérieur, comme dans la figure 10.48. Au milieu, la même unité cubique avec des molécules sphériques superposées, comme dans la rangée du bas de la figure 10.48. A droite, les molécules grises qui sont à l'extérieur du cube sont rasées, ne laissant que des portions de molécules grises et six moitiés de molécules rouges (puisqu'elles ont été divisées en deux).

Figure 7. Un solide cubique à faces centrées a des atomes aux coins et, comme son nom l’indique, au centre des faces de ses cellules unitaires.

Les atomes dans un arrangement FCC sont emballés aussi étroitement que possible, les atomes occupant 74% du volume. Cette structure est également appelée cubic closest packing (CCP). Dans la structure CCP, il y a trois couches répétées d’atomes disposés de façon hexagonale. Chaque atome touche six atomes dans sa propre couche, trois dans la couche supérieure et trois dans la couche inférieure. Dans cet arrangement, chaque atome touche 12 voisins proches, et a donc un nombre de coordination de 12. Le fait que les arrangements FCC et CCP sont équivalents peut ne pas être immédiatement évident, mais la raison pour laquelle ils sont en fait la même structure est illustrée dans la figure 8.

Trois images sont montrées. Dans la première image, une vue latérale montre une couche de sphères bleues, étiquetées

Figure 8. Un arrangement CCP consiste en trois couches répétées (ABCABC…) d’atomes disposés de façon hexagonale. Les atomes d’une structure CCP ont un nombre de coordination de 12 car ils sont en contact avec six atomes de leur couche, plus trois atomes de la couche supérieure et trois atomes de la couche inférieure. En tournant notre perspective, nous pouvons voir qu’une structure CCP a une cellule unitaire avec une face contenant un atome de la couche A à un coin, des atomes de la couche B sur une diagonale (à deux coins et au milieu de la face), et un atome de la couche C au coin restant. C’est la même chose qu’un arrangement cubique à faces centrées.

Parce que l’emballage le plus serré maximise les attractions globales entre les atomes et minimise l’énergie intermoléculaire totale, les atomes de la plupart des métaux s’emballent de cette manière. Nous trouvons deux types d’empilement le plus serré dans les structures cristallines métalliques simples : Le CCP, que nous avons déjà rencontré, et le closeest packing hexagonal (HCP) illustré à la figure 9. Tous deux consistent en des couches répétées d’atomes disposés en hexagone. Dans les deux types, une deuxième couche (B) est placée sur la première couche (A) de sorte que chaque atome de la deuxième couche est en contact avec trois atomes de la première couche. La troisième couche est positionnée de l’une des deux manières suivantes. Dans le cas du HCP, les atomes de la troisième couche sont directement au-dessus des atomes de la première couche (c’est-à-dire que la troisième couche est également de type A), et l’empilement est constitué de couches empilées de type A et de type B alternées (c’est-à-dire ABABAB⋯). Dans le cas du CCP, les atomes de la troisième couche ne se trouvent pas au-dessus des atomes des deux premières couches (c’est-à-dire que la troisième couche est de type C), et l’empilement est constitué de couches empilées alternées de type A, de type B et de type C (c’est-à-dire ABCABCABC⋯). Environ deux tiers de tous les métaux cristallisent en réseaux les plus compacts avec des numéros de coordination de 12. Les métaux qui cristallisent dans une structure HCP comprennent Cd, Co, Li, Mg, Na et Zn, et les métaux qui cristallisent dans une structure CCP comprennent Ag, Al, Ca, Cu, Ni, Pb et Pt.

Deux images sont présentées. La première image, étiquetée

Figure 9. Dans les deux types d’emballage le plus serré, les atomes sont emballés de manière aussi compacte que possible. Le closest packing hexagonal est constitué de deux couches alternées (ABABAB…). L’emballage le plus serré cubique consiste en trois couches alternées (ABCABCABC…).

Exemple 2 : Calcul du rayon atomique et de la densité pour les métaux, partie 2

Le calcium cristallise dans une structure cubique à faces centrées. La longueur d’arête de sa cellule unitaire est de 558,8 pm.

  1. Quel est le rayon atomique du Ca dans cette structure ?
  2. Calculez la densité du Ca.
Afficher la solution

Partie 1

Deux dessins sont présentés. A droite, "hexagonal le plus serré", on voit une vue de côté de 4 rangées de sphères. La couche supérieure et la troisième couche sont vertes, tandis que la 2e et la 4e couche sont bleues. Sur la droite, "cubic closest packed", nous voyons une vue latérale de quatre rangées de sphères. La rangée supérieure et la rangée inférieure sont bleues (la couche supérieure est appelée couche C). La 2e rangée est verte, et étiquetée couche B. La troisième rangée est violette, et étiquetée couche A.

Dans une structure FCC, les atomes de Ca se contactent à travers la diagonale de la face, de sorte que la longueur de la diagonale est égale à quatre rayons atomiques de Ca (d = 4r). Deux bords adjacents et la diagonale de la face forment un triangle rectangle, dont la longueur de chaque côté est égale à 558,8 pm et la longueur de l’hypoténuse est égale à quatre rayons atomiques de Ca :

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}\long-flèche droite {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}{16}=\text{197,6 pmg pour un rayon de Ca}.

Partie 2

La densité est donnée par \text{densité}=\dfrac{\text{masse}}{\text{volume}. La densité du calcium peut être trouvée en déterminant la densité de sa cellule unitaire : par exemple, la masse contenue dans une cellule unitaire divisée par le volume de la cellule unitaire. Une cellule unitaire de Ca à faces centrées comporte un huitième d’atome à chacun des huit coins \left(8\times \dfrac{1}{8}=1\text{ atom}\right) et un demi-atome sur chacune des six faces \left(6\times \dfrac{1}{2}=3\text{ atoms}\right), soit un total de quatre atomes dans la cellule unitaire.

La masse de la cellule unitaire peut être trouvée par:

\text{1 cellule unitaire de Ca}\times \dfrac{\text{4 atomes de Ca}{\text{1 cellule unitaire de Ca}\times \dfrac{\text{1 mol Ca}{6.022\times {10}^{23}\text{\c} atomes de Ca}\times \dfrac{40.078\text{g}{\text{1 mol Ca}}=2.662\times {10}^{-22}\text{g}

Le volume d’une cellule unitaire de Ca peut être trouvé par:

V={a}^{3}={(558.8\times {10}^{-10}\text{cm})}^{3}=1.745\times {10}^{-22}{\text{cm}}^{3}

(Notez que la longueur du bord a été convertie de pm en cm pour obtenir les unités de volume habituelles pour la densité.)

Alors, la densité de \text{Ca}=\dfrac{2.662\times {10}^{-22}\text{g}}{1.745\times {10}^{-22}{\text{cm}}^{3}={\text{1.53 g/cm}}^{3}

Vérifiez vos acquis

L’argent cristallise dans une structure FCC. La longueur d’arête de sa cellule unitaire est de 409 pm.

  1. Quel est le rayon atomique de l’Ag dans cette structure ?
  2. Calculez la densité de l’Ag.
Afficher les solutions

  1. 144 pm
  2. 10.5 g/cm3

En général, une cellule unitaire est définie par les longueurs de trois axes (a, b, et c) et les angles (α, β, et γ) entre eux, comme illustré dans la figure 10. Les axes sont définis comme étant les longueurs entre les points du réseau spatial. Par conséquent, les axes des cellules unitaires rejoignent des points ayant des environnements identiques.

Un dessin d'une unité cubique est montré, avec les points du treillis. Les plans de la surface du cube sont étiquetés a, b, et c. Un cercle de flèches apparaît autour d'un point de treillis, étiqueté (α, β, et γ).

Figure 10. Une cellule unitaire est définie par les longueurs de ses trois axes (a, b, et c) et les angles (α, β, et γ) entre les axes.

Il existe sept systèmes de treillis différents, dont certains ont plus d’un type de treillis, pour un total de quatorze cellules unitaires différentes, qui ont les formes indiquées dans la figure 11.

Tableau de 7 lignes, avec deux colonnes intitulées Système/Axes/Angles et Cellules unitaires.

Figure 11. Il existe sept systèmes de réseau différents et 14 cellules unitaires différentes.

Les structures des cristaux ioniques

Les cristaux ioniques sont constitués de deux ou plusieurs types d’ions différents qui ont généralement des tailles différentes. L’emballage de ces ions dans une structure cristalline est plus complexe que l’emballage d’atomes métalliques de même taille.

La plupart des ions monatomiques se comportent comme des sphères chargées, et leur attraction pour les ions de charge opposée est la même dans toutes les directions. Par conséquent, les structures stables des composés ioniques résultent (1) lorsque les ions d’une charge sont entourés par autant d’ions que possible de la charge opposée et (2) lorsque les cations et les anions sont en contact les uns avec les autres. Les structures sont déterminées par deux facteurs principaux : les tailles relatives des ions et le rapport du nombre d’ions positifs et négatifs dans le composé.

Une image montre une vue de dessus d'une couche de sphères bleues disposées dans une feuille reposant sur une autre feuille identique sauf que les sphères sont vertes. La deuxième feuille est décalée juste un peu de sorte que les sphères de la feuille supérieure se trouvent dans les rainures de la deuxième feuille. Une troisième feuille composée de sphères violettes se trouve en bas. Les espaces créés entre les sphères de chaque couche sont étiquetés

Figure 12. Les cations peuvent occuper deux types de trous entre les anions : les trous octaédriques ou les trous tétraédriques.

Dans les structures ioniques simples, on trouve généralement les anions, qui sont normalement plus grands que les cations, disposés dans un réseau le plus serré. (Comme nous l’avons vu précédemment, des électrons supplémentaires attirés par le même noyau rendent les anions plus grands et moins d’électrons attirés par le même noyau rendent les cations plus petits par rapport aux atomes à partir desquels ils sont formés). Les cations plus petits occupent généralement l’un des deux types de trous (ou interstices) restant entre les anions. Le plus petit de ces trous se trouve entre trois anions dans un plan et un anion dans un plan adjacent. Les quatre anions entourant ce trou sont disposés aux angles d’un tétraèdre, le trou est donc appelé trou tétraédrique. Le plus grand type de trou se trouve au centre de six anions (trois dans une couche et trois dans une couche adjacente) situés aux coins d’un octaèdre ; on l’appelle un trou octaédrique. La figure 12 illustre ces deux types de trous.

Selon les tailles relatives des cations et des anions, les cations d’un composé ionique peuvent occuper des trous tétraédriques ou octaédriques, comme l’illustre la figure 13. Les cations relativement petits occupent des trous tétraédriques, et les cations plus grands occupent des trous octaédriques. Si les cations sont trop grands pour entrer dans les trous octaédriques, les anions peuvent adopter une structure plus ouverte, comme un simple réseau cubique. Les plus grands cations peuvent alors occuper les plus grands trous cubiques rendus possibles par l’espacement plus ouvert.

Trois dessins de cube de réseau sont donnés. À gauche, l'unité cubique inférieure gauche a des points de treillis verts, tous les autres cubes ayant des points violets (étiquetés Trou tétraédrique). Au milieu, les points du treillis sont soit verts soit orange, sur une ligne diagonale (étiqueté trou octaédrique). A droite, tous les points du treillis sont violets, étiquetés Trou cubique.

Figure 13. La taille d’un cation et la forme du trou occupé par le composé sont directement liées.

Il y a deux trous tétraédriques pour chaque anion dans un réseau d’anions HCP ou CCP. Un composé qui cristallise dans un réseau d’anions le plus étroitement empaqueté avec des cations dans les trous tétraédriques peut avoir un rapport maximum cation:anion de 2:1 ; tous les trous tétraédriques sont remplis à ce rapport. Les exemples incluent Li2O, Na2O, Li2S et Na2S. Les composés dont le rapport est inférieur à 2:1 peuvent également cristalliser dans un réseau le plus proche des anions avec des cations dans les trous tétraédriques, si les tailles ioniques correspondent. Dans ces composés, cependant, certains des trous tétraédriques restent vacants.

Exemple 3 : Occupation des trous tétraédriques

Le sulfure de zinc est une source industrielle importante de zinc et est également utilisé comme pigment blanc dans la peinture. Le sulfure de zinc cristallise avec des ions zinc occupant la moitié des trous tétraédriques dans un réseau d’ions sulfure les plus serrés. Quelle est la formule du sulfure de zinc ?

Montrer la solution

Parce qu’il y a deux trous tétraédriques par anion (ion sulfure) et que la moitié de ces trous sont occupés par des ions zinc, il doit y avoir \frac{1}{2}\times 2, ou 1, ion zinc par ion sulfure. Ainsi, la formule est ZnS.

Vérifiez vos acquis

Le séléniure de lithium peut être décrit comme un réseau d’ions séléniures le plus serré avec des ions lithium dans tous les trous tétraédriques. Quelle est la formule du séléniure de lithium ?

Montrer la solution

Li2Se

Le rapport entre les trous octaédriques et les anions dans une structure HCP ou CCP est de 1:1. Ainsi, les composés avec des cations dans les trous octaédriques dans un réseau d’anions les plus proches peuvent avoir un rapport maximum cation:anion de 1:1. Dans NiO, MnS, NaCl et KH, par exemple, tous les trous octaédriques sont remplis. Des rapports inférieurs à 1:1 sont observés lorsque certains des trous octaédriques restent vides.

Exemple 4 : Stœchiométrie des composés ioniques

Le saphir est un oxyde d’aluminium. L’oxyde d’aluminium cristallise avec des ions aluminium dans les deux tiers des trous octaédriques dans un réseau d’ions d’oxyde le plus serré. Quelle est la formule de l’oxyde d’aluminium ?

Montrer la solution

Parce qu’il y a un trou octaédrique par anion (ion oxyde) et que seulement deux tiers de ces trous sont occupés, le rapport de l’aluminium à l’oxygène doit être \frac{2}{3} :1, ce qui donnerait {\text{Al}}_{2\text{/}3}\text{O}. Le rapport le plus simple en nombre entier est 2:3, la formule est donc Al2O3.

Vérifiez vos acquis

Le pigment blanc qu’est l’oxyde de titane cristallise avec des ions titane dans la moitié des trous octaédriques dans un réseau d’ions oxyde les plus proches. Quelle est la formule de l’oxyde de titane ?

Montrer la solution

TiO2

Dans un réseau cubique simple d’anions, il y a un trou cubique qui peut être occupé par un cation pour chaque anion du réseau. Dans le CsCl, et dans d’autres composés de même structure, tous les trous cubiques sont occupés. La moitié des trous cubiques sont occupés dans le SrH2, l’UO2, le SrCl2 et le CaF2.

Des types différents de composés ioniques cristallisent souvent dans la même structure lorsque les tailles relatives de leurs ions et leurs stœchiométries (les deux principales caractéristiques qui déterminent la structure) sont similaires.

Cellules unitaires des composés ioniques

De nombreux composés ioniques cristallisent avec des cellules unitaires cubiques, et nous utiliserons ces composés pour décrire les caractéristiques générales des structures ioniques.

Lorsqu’un composé ionique est composé de cations et d’anions de taille similaire dans un rapport 1:1, il forme généralement une structure cubique simple. Le chlorure de césium, CsCl, (illustré à la figure 14) en est un exemple, le Cs+ et le Cl- ayant des rayons de 174 pm et 181 pm, respectivement. On peut considérer que les ions chlorure forment une cellule unitaire cubique simple, avec un ion césium au centre, ou que les ions césium forment une cellule unitaire avec un ion chlorure au centre, ou encore que les cellules unitaires cubiques simples formées par les ions Cs+ recouvrent les cellules unitaires formées par les ions Cl-. Les ions césium et les ions chlorure se touchent le long des diagonales du corps des cellules unitaires. Un ion césium et un ion chlorure sont présents par cellule unitaire, ce qui donne la stœchiométrie l:l requise par la formule du chlorure de césium. Notez qu’il n’y a pas de point de réseau au centre de la cellule, et que CsCl n’est pas une structure BCC car un ion césium n’est pas identique à un ion chlorure.

Trois dessins sont présentés. A gauche, un rendu d'unités cubiques infinies, le cube inférieur gauche contenant un point rouge en son centre. Au milieu, ce seul cube apparaît, avec les points du réseau sous forme de grosses sphères violettes. La molécule centrale est plus petite, et verte. À droite, un empilement de cubes de sphères violettes apparaît, avec de petites sphères vertes entre elles montrant sur un côté.

Figure 14. Les composés ioniques avec des cations et des anions de taille similaire, comme le CsCl, forment généralement une structure cubique simple. Ils peuvent être décrits par des cellules unitaires avec soit des cations aux coins, soit des anions aux coins.

Nous avons dit que l’emplacement des points du réseau est arbitraire. Ceci est illustré par une description alternative de la structure du CsCl dans laquelle les points de réseau sont situés dans les centres des ions césium. Dans cette description, les ions césium sont situés sur les points du réseau aux coins de la cellule, et l’ion chlorure est situé au centre de la cellule. Les deux cellules unitaires sont différentes, mais elles décrivent des structures identiques.

Lorsqu’un composé ionique est composé d’un rapport 1:1 de cations et d’anions qui diffèrent significativement en taille, il cristallise généralement avec une cellule unitaire FCC, comme celle présentée dans la figure 15. Le chlorure de sodium, NaCl, en est un exemple, avec Na+ et Cl- ayant des rayons de 102 pm et 181 pm, respectivement. Nous pouvons considérer que les ions chlorure forment une cellule FCC, avec des ions sodium situés dans les trous octaédriques au milieu des bords de la cellule et au centre de la cellule. Les ions sodium et chlorure se touchent le long des bords de la cellule. La cellule unitaire contient quatre ions sodium et quatre ions chlorure, ce qui donne la stœchiométrie 1:1 requise par la formule, NaCl.

Trois images sont montrées. La première image montre un cube avec des points noirs à chaque coin et un point rouge au centre. Ce cube est empilé avec sept autres qui ne sont pas colorés pour former un cube plus grand. La deuxième image est composée de huit sphères qui sont regroupées pour former un cube avec une sphère beaucoup plus grande au centre. Le nom sous cette image se lit comme suit

Figure 15. Les composés ioniques dont les anions sont beaucoup plus grands que les cations, comme le NaCl, forment généralement une structure FCC. Ils peuvent être décrits par des cellules unitaires FCC avec des cations dans les trous octaédriques.

La forme cubique du sulfure de zinc, la blende de zinc, cristallise également dans une cellule unitaire FCC, comme illustré dans la figure 16. Cette structure contient des ions sulfure sur les points de réseau d’un réseau FCC. (La disposition des ions sulfure est identique à celle des ions chlorure dans le chlorure de sodium). Le rayon d’un ion zinc ne représente qu’environ 40 % du rayon d’un ion sulfure, de sorte que ces petits ions Zn2+ sont situés dans des trous tétraédriques alternés, c’est-à-dire dans une moitié des trous tétraédriques. Il y a quatre ions zinc et quatre ions sulfure dans la cellule unitaire, ce qui donne la formule empirique ZnS.

Deux dessins apparaissent. A gauche, une structure cubique infinie est rendue, le cube inférieur gauche contenant six points rouges. A droite, ce seul cube est agrandi, et des points jaunes apparaissent à intervalles aléatoires sur les bords et à l'intérieur du cube, pour représenter les points du réseau.

Figure 16. ZnS, le sulfure de zinc (ou blende de zinc) forme une cellule unitaire FCC avec des ions sulfure aux points de réseau et des ions zinc beaucoup plus petits occupant la moitié des trous tétraédriques de la structure.

Une cellule unitaire de fluorure de calcium, comme celle représentée sur la figure 17, est également une cellule unitaire FCC, mais dans ce cas, les cations sont situés sur les points de réseau ; des ions calcium équivalents sont situés sur les points de réseau d’un réseau FCC. Tous les sites tétraédriques du réseau FCC des ions calcium sont occupés par des ions fluorure. Il y a quatre ions calcium et huit ions fluorure dans une cellule unitaire, ce qui donne un rapport calcium:fluor de l:2, comme l’exige la formule chimique CaF2. Un examen attentif de la figure 17 révèle un simple réseau cubique d’ions fluorure avec des ions calcium dans la moitié des trous cubiques. La structure ne peut pas être décrite en termes de treillis spatial de points sur les ions fluorure car les ions fluorure n’ont pas tous un environnement identique. L’orientation des quatre ions calcium autour des ions fluorure diffère.

Deux dessins apparaissent. A gauche, le rendu d'une structure cubique infinie, dont le cube inférieur gauche contient six points rouges. A droite, ce seul cube est agrandi pour montrer de nombreuses sphères vertes, aux coins du cube et à l'intérieur. Toutes sont reliées par des lignes. Cellule unitaire CaF2 à faces centrées étiquetée.

Figure 17. Le fluorure de calcium, CaF2, forme une cellule unitaire FCC avec des ions calcium (vert) aux points du réseau et des ions fluorure (rouge) occupant tous les sites tétraédriques entre eux.

Calcul des rayons ioniques

Si l’on connaît la longueur d’arête d’une cellule unitaire d’un composé ionique et la position des ions dans la cellule, on peut calculer les rayons ioniques des ions du composé si l’on fait des hypothèses sur les formes et les contacts ioniques individuels.

Exemple 5 : Calcul des rayons ioniques

La longueur de bord de la cellule unitaire de LiCl (structure de type NaCl, FCC) est de 0.514 nm ou 5,14 Å. En supposant que l’ion lithium est suffisamment petit pour que les ions chlorure soient en contact, comme dans la figure 15, calculez le rayon ionique de l’ion chlorure.

Note : L’unité de longueur angstrom, Å, est souvent utilisée pour représenter les dimensions à l’échelle atomique et est équivalente à 10-10 m.

Montrer la solution

Sur la face d’une cellule unitaire de LiCl, les ions chlorure se contactent sur la diagonale de la face :

Trois images sont présentées. La première montre un cube de sphères alternativement vertes et violettes. Un plus petit cube à l'intérieur de ce cube est décrit et une version plus grande de celui-ci apparaît ensuite. Cette figure est un cube gris qui semble être composé de sphères. Il y a de petits espaces entre chaque sphère. Un triangle rectangle est dessiné dans ce cube et une version plus grande de celui-ci apparaît ensuite. Ce triangle rectangle a deux côtés étiquetés

Dessinant un triangle rectangle sur la face de la cellule unitaire, nous voyons que la longueur de la diagonale est égale à quatre rayons de chlorure (un rayon de chaque chlorure d’angle et un diamètre – qui équivaut à deux rayons – de l’ion chlorure au centre de la face), donc d = 4r. D’après le théorème de Pythagore, on a :

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}

ce qui donne :

\gauche(0,514\text{ nm}\droite)^{2}+\gauche(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) pour un rayon Cl-

Vérifiez votre apprentissage

La longueur du bord de la cellule unitaire de KCl (structure de type NaCl, FCC) est de 6,28 Å. En supposant un contact anion-cation le long du bord de la cellule, calculez le rayon de l’ion potassium. Le rayon de l’ion chlorure est de 1,82 Å.

Montrer la solution

Le rayon de l’ion potassium est de 1,33 Å.

Il est important de réaliser que les valeurs des rayons ioniques calculées à partir des longueurs des bords des cellules unitaires dépendent de nombreuses hypothèses, telles qu’une forme sphérique parfaite pour les ions, qui sont au mieux des approximations. Par conséquent, ces valeurs calculées sont elles-mêmes approximatives et les comparaisons ne peuvent être poussées trop loin. Néanmoins, cette méthode s’est avérée utile pour calculer les rayons ioniques à partir de mesures expérimentales telles que les déterminations cristallographiques aux rayons X.

Cristallographie aux rayons X

La taille de la cellule unitaire et l’arrangement des atomes dans un cristal peuvent être déterminés à partir de mesures de la diffraction des rayons X par le cristal, ce que l’on appelle la cristallographie aux rayons X. La diffraction est la modification de la direction de déplacement d’une onde électromagnétique lorsqu’elle rencontre une barrière physique dont les dimensions sont comparables à celles de la longueur d’onde de la lumière. Les rayons X sont des radiations électromagnétiques dont la longueur d’onde est à peu près aussi longue que la distance entre atomes voisins dans les cristaux (de l’ordre de quelques Å).

Lorsqu’un faisceau de rayons X monochromatiques frappe un cristal, ses rayons sont diffusés dans toutes les directions par les atomes du cristal. Lorsque des ondes diffusées se déplaçant dans la même direction se rencontrent, elles subissent des interférences, un processus par lequel les ondes se combinent pour donner une augmentation ou une diminution de l’amplitude (intensité) selon la mesure dans laquelle les maxima des ondes qui se combinent sont séparés (voir figure 18).

On montre une paire d'images qui comporte quatre sections. Dans la première section, deux ondes sinusoïdales sont montrées, une dessinée au-dessus de l'autre, et une section allant du sommet d'une courbe au sommet de la courbe suivante est étiquetée

Figure 18. Les ondes lumineuses occupant le même espace subissent des interférences, se combinant pour donner des ondes de plus grande (a) ou de moindre (b) intensité, selon la séparation de leurs maxima et minima.

Lorsque des rayons X d’une certaine longueur d’onde, λ, sont diffusés par des atomes dans des plans cristallins adjacents séparés par une distance, d, ils peuvent subir des interférences constructives lorsque la différence entre les distances parcourues par les deux ondes avant leur combinaison est un facteur entier, n, de la longueur d’onde. Cette condition est satisfaite lorsque l’angle du faisceau diffracté, θ, est lié à la longueur d’onde et à la distance interatomique par l’équation :

n{\lambda }=2d\text{sin}\theta

Cette relation est connue sous le nom d’équation de Bragg en l’honneur de W. H. Bragg, le physicien anglais qui a été le premier à expliquer ce phénomène. La figure 19 illustre deux exemples d’ondes diffractées à partir des deux mêmes plans cristallins. La figure de gauche représente des ondes diffractées à l’angle de Bragg, ce qui entraîne une interférence constructive, tandis que celle de droite montre la diffraction et un angle différent qui ne satisfait pas la condition de Bragg, ce qui entraîne une interférence destructive.

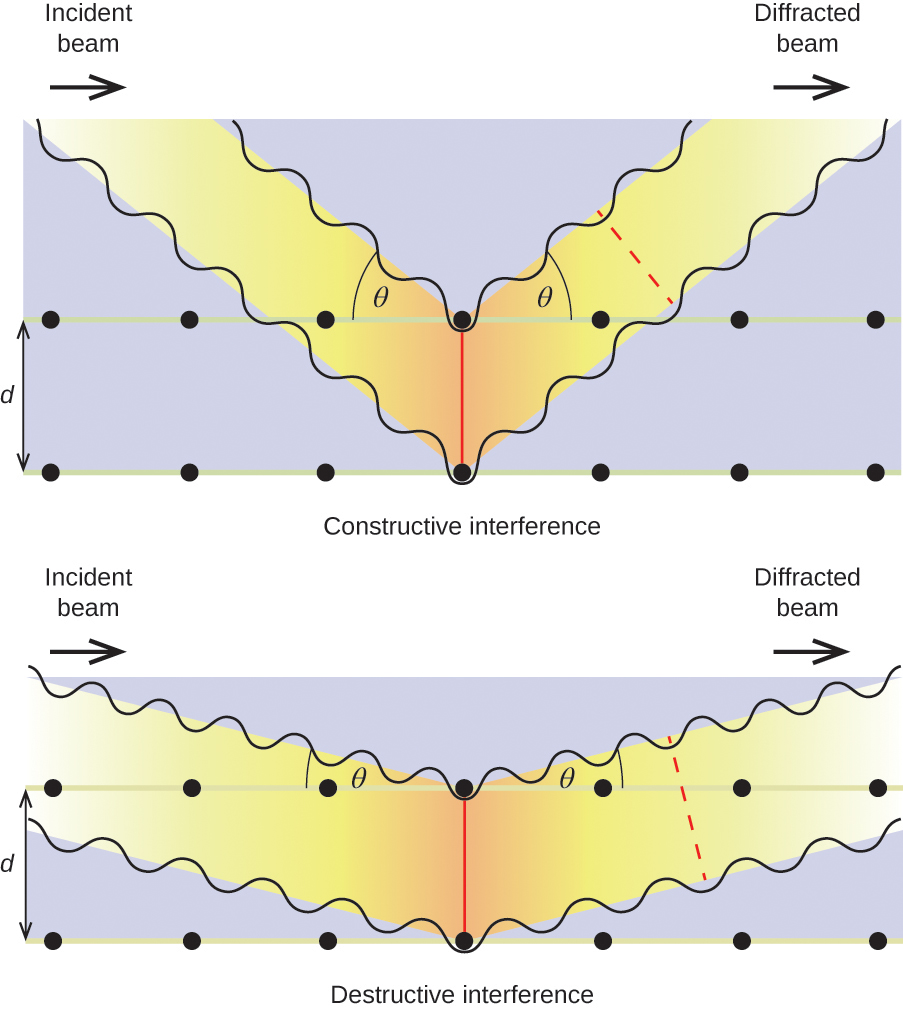
Deux figures similaires sont présentées. La première figure, étiquetée

Figure 19. La diffraction des rayons X diffusés par les atomes à l’intérieur d’un cristal permet de déterminer la distance entre les atomes. L’image du haut représente une interférence constructive entre deux ondes diffusées et une onde diffractée résultante de forte intensité. L’image du bas représente une interférence destructive et une onde diffractée de faible intensité.

Visitez « Qu’est-ce que la loi de Bragg et pourquoi est-elle importante ? » pour plus de détails sur l’équation de Bragg et un simulateur qui vous permet d’explorer l’effet de chaque variable sur l’intensité de l’onde diffractée.

Un diffractomètre à rayons X, tel que celui illustré à la figure 20, peut être utilisé pour mesurer les angles auxquels les rayons X sont diffractés lorsqu’ils interagissent avec un cristal comme décrit ci-dessus. A partir de ces mesures, l’équation de Bragg peut être utilisée pour calculer les distances entre les atomes, comme le montre l’exemple d’exercice suivant.

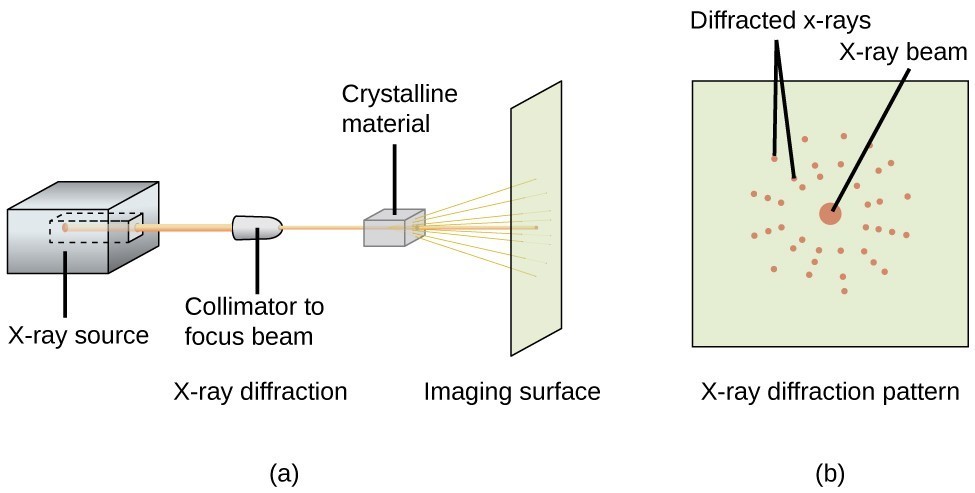
Deux séries de dessins sont données. A droite, a) est une vue latérale d'une projection de rayons X d'une machine vers le mur, traversant un matériau cristallin. A droite, b) est une image de face du mur, montrant le faisceau de rayons X et les rayons X diffractés qui en résultent.

Figure 20. Dans un diffractomètre (a), un faisceau de rayons X frappe un matériau cristallin, produisant un diagramme de diffraction des rayons X (b) qui peut être analysé pour déterminer la structure cristalline.

Vous pouvez consulter la transcription de « Celebrating Crystallography – An animated adventure » ici (s’ouvre dans une nouvelle fenêtre).

Exemple 6 : Utilisation de l’équation de Bragg

Dans un diffractomètre, des rayons X d’une longueur d’onde de 0,1315 nm ont été utilisés pour produire un diagramme de diffraction du cuivre. La diffraction de premier ordre (n = 1) s’est produite à un angle θ = 25,25°. Déterminez l’espacement entre les plans de diffraction dans le cuivre.

Afficher la solution

La distance entre les plans est trouvée en résolvant l’équation de Bragg, nλ = 2d sin θ, pour d.

Cela donne : d=\dfrac{n\lambda}{2\sin\theta}=\dfrac{1\left(0.1315\text{ nm}\right)}{2\sin\left(25,25^{\circ}\right)}=0,154\text{ nm}

Check Your Learning

Un cristal dont l’espacement entre les plans est égal à 0,394 nm diffracte les rayons X avec une longueur d’onde de 0,147 nm. Quel est l’angle de diffraction de premier ordre ?

Afficher la solution

10,8°

Portrait d’une chimiste : Rosalind Franklin, cristallographe aux rayons X

Cette image montre une illustration circulaire avec des anneaux de points qui sont flous entre eux.

Figure 21. Cette illustration montre une image de diffraction de rayons X similaire à celle que Franklin a trouvée dans ses recherches. (crédit : National Institutes of Health)

La découverte de la structure de l’ADN en 1953 par Francis Crick et James Watson est l’une des grandes réalisations de l’histoire des sciences. Ils ont reçu le prix Nobel de physiologie ou de médecine en 1962, avec Maurice Wilkins, qui a apporté la preuve expérimentale de la structure de l’ADN. La chimiste britannique Rosalind Franklin a apporté une contribution inestimable à cette réalisation monumentale grâce à son travail de mesure des images de diffraction des rayons X de l’ADN. Au début de sa carrière, les recherches de Mme Franklin sur la structure des charbons se sont avérées utiles à l’effort de guerre britannique. Après s’être intéressée aux systèmes biologiques au début des années 1950, Mme Franklin et son doctorant Raymond Gosling ont découvert que l’ADN se présente sous deux formes : une fibre longue et fine formée lorsqu’elle est humide (type « B ») et une fibre courte et large formée lorsqu’elle est sèche (type « A »). Ses images de l’ADN obtenues par diffraction des rayons X (figure 21) ont fourni les informations cruciales qui ont permis à Watson et Crick de confirmer que l’ADN forme une double hélice, et de déterminer les détails de sa taille et de sa structure.

Franklin a également mené des recherches pionnières sur les virus et l’ARN qui contient leur information génétique, découvrant de nouvelles informations qui ont radicalement changé l’ensemble des connaissances dans ce domaine. Après avoir développé un cancer des ovaires, Franklin a continué à travailler jusqu’à sa mort en 1958 à l’âge de 37 ans. Parmi les nombreuses reconnaissances posthumes de son travail, l’école de médecine de Chicago de l’Université Finch des sciences de la santé a changé son nom pour devenir l’Université Rosalind Franklin de médecine et de science en 2004, et a adopté une image de sa célèbre image de diffraction des rayons X de l’ADN comme logo officiel de l’université.

Concepts clés et résumé

Les structures des métaux cristallins et des composés ioniques simples peuvent être décrites en termes d’emballage de sphères. Les atomes métalliques peuvent s’empaqueter dans des structures hexagonales les plus proches, des structures cubiques les plus proches, des structures centrées sur le corps et des structures cubiques simples. Les anions des structures ioniques simples adoptent généralement l’une de ces structures, et les cations occupent les espaces restants entre les anions. Les petits cations occupent généralement des trous tétraédriques dans un réseau d’anions les plus proches les uns des autres. Les cations plus grands occupent généralement des trous octaédriques. Des cations encore plus grands peuvent occuper des trous cubiques dans un réseau cubique simple d’anions. La structure d’un solide peut être décrite en indiquant la taille et la forme d’une cellule unitaire et le contenu de la cellule. Le type de structure et les dimensions de la cellule unitaire peuvent être déterminés par des mesures de diffraction des rayons X.

Équations clés

  • n{\lambda }=2d\text{sin}\theta

Try It

  1. Décrire la structure cristalline du fer, qui cristallise avec deux atomes métalliques équivalents dans une cellule unitaire cubique.
  2. Décrivez la structure cristalline du Pt, qui cristallise avec quatre atomes métalliques équivalents dans une cellule unitaire cubique.
  3. Quel est le nombre de coordination d’un atome de chrome dans la structure cubique centrée sur le corps du chrome ?
  4. Quel est le nombre de coordination d’un atome d’aluminium dans la structure cubique centrée sur la face de l’aluminium ?
  5. Le cobalt métallique cristallise dans une structure hexagonale la plus serrée. Quel est le nombre de coordination d’un atome de cobalt?
  6. Le nickel métallique cristallise dans une structure cubique la plus condensée. Quel est le nombre de coordination d’un atome de nickel ?
  7. Le tungstène cristallise dans une cellule unitaire cubique centrée sur le corps avec une longueur d’arête de 3,165 Å.
    1. Quel est le rayon atomique du tungstène dans cette structure ?
    2. Calculez la densité du tungstène.
  8. Le platine (rayon atomique = 1,38 Å) cristallise dans une structure cubique très tassée. Calculez la longueur d’arête de la cellule unitaire cubique à faces centrées et la densité du platine.
  9. Le baryum cristallise dans une cellule unitaire cubique à corps centré dont la longueur d’arête est de 5.025 Å
    1. Quel est le rayon atomique du baryum dans cette structure ?
    2. Calculez la densité du baryum.
  10. L’aluminium (rayon atomique = 1,43 Å) cristallise dans une structure cubique très compacte. Calculez la longueur d’arête de la cellule unitaire cubique à faces centrées et la densité de l’aluminium.
  11. La densité de l’aluminium est de 2,7 g/cm3 ; celle du silicium est de 2,3 g/cm3. Expliquez pourquoi le Si a la plus faible densité même s’il a des atomes plus lourds.
  12. L’espace libre dans un métal peut être trouvé en soustrayant le volume des atomes dans une cellule unitaire du volume de la cellule. Calculez le pourcentage d’espace libre dans chacun des trois treillis cubiques si tous les atomes de chacun sont de taille égale et touchent leurs voisins les plus proches. Laquelle de ces structures représente l’empilement le plus efficace ? C’est-à-dire, laquelle s’entasse avec le moins d’espace inutilisé ?
  13. Le sulfure de cadmium, parfois utilisé comme pigment jaune par les artistes, cristallise avec le cadmium, occupant la moitié des trous tétraédriques dans un réseau le plus serré d’ions sulfure. Quelle est la formule du sulfure de cadmium ? Expliquez votre réponse.
  14. Un composé de cadmium, d’étain et de phosphore est utilisé dans la fabrication de certains semi-conducteurs. Il cristallise avec le cadmium occupant un quart des trous tétraédriques et l’étain occupant un quart des trous tétraédriques dans un réseau le plus serré d’ions phosphure. Quelle est la formule de ce composé ? Expliquez votre réponse.
  15. Quelle est la formule de l’oxyde magnétique de cobalt, utilisé dans les bandes d’enregistrement, qui cristallise avec des atomes de cobalt occupant un huitième des trous tétraédriques et la moitié des trous octaédriques dans un réseau serré d’ions oxyde ?
  16. Un composé contenant du zinc, de l’aluminium et du soufre cristallise avec un réseau serré d’ions sulfure. Les ions zinc se trouvent dans un huitième des trous tétraédriques et les ions aluminium dans la moitié des trous octaédriques. Quelle est la formule empirique de ce composé ?
  17. Un composé de thallium et d’iode cristallise dans un réseau cubique simple d’ions iodure avec des ions thallium dans tous les trous cubiques. Quelle est la formule de cet iodure ? Expliquez votre réponse.
  18. Quel élément parmi les suivants réagit avec le soufre pour former un solide dans lequel les atomes de soufre forment un réseau le plus serré avec tous les trous octaédriques occupés : Li, Na, Be, Ca ou Al ?
  19. Quel est le pourcentage en masse de titane dans le rutile, un minéral qui contient du titane et de l’oxygène, si la structure peut être décrite comme un réseau le plus serré d’ions oxyde avec des ions titane dans la moitié des trous octaédriques ? Quel est le nombre d’oxydation du titane ?
  20. Expliquez pourquoi les chlorures de métaux alcalins chimiquement similaires NaCl et CsCl ont des structures différentes, alors que les chlorures chimiquement différents NaCl et MnS ont la même structure.
  21. Lorsque les minéraux se sont formés à partir du magma fondu, différents ions ont occupé les mêmes cites dans les cristaux. Le lithium est souvent présent avec le magnésium dans les minéraux malgré la différence de charge de leurs ions. Proposez une explication.
  22. L’iodure de rubidium cristallise avec une cellule unitaire cubique qui contient des ions iodure aux coins et un ion rubidium au centre. Quelle est la formule du composé ?
  23. L’un des différents oxydes de manganèse cristallise avec une cellule unitaire cubique qui contient des ions manganèse aux coins et au centre. Les ions d’oxyde sont situés au centre de chaque bord de la cellule unitaire. Quelle est la formule du composé ?
  24. NaH cristallise avec la même structure cristalline que NaCl. La longueur de l’arête de la cellule unitaire cubique de NaH est de 4,880 Å.
    1. Calculez le rayon ionique de H-. (Le rayon ionique de Li+ est de 0,0,95 Å.)
    2. Calculez la densité de NaH.
  25. L’iodure de thallium(I) cristallise avec la même structure que le CsCl. La longueur de l’arête de la cellule unitaire de TlI est de 4,20 Å.
    1. Calculez le rayon ionique de TI+. (Le rayon ionique de I- est de 2,16 Å.)
    2. Calculez la densité de TlI.
  26. Une cellule unitaire cubique contient des ions manganèse aux coins et des ions fluorure au centre de chaque bord.
    1. Quelle est la formule empirique de ce composé ? Expliquez votre réponse.
    2. Quel est le numéro de coordination de l’ion Mn3+ ?
    3. Calculez la longueur du bord de la cellule unitaire si le rayon d’un ion Mn3+ est de 0,65 A.
    4. Calculez la densité du composé.
  27. Quel est l’espacement entre les plans cristallins qui diffractent les rayons X avec une longueur d’onde de 1,541 nm à un angle θ de 15,55° (réflexion de premier ordre) ?
  28. Un diffractomètre utilisant des rayons X avec une longueur d’onde de 0,2287 nm a produit un pic de diffraction de premier ordre pour un angle cristallin θ = 16,21°. Déterminez l’espacement entre les plans de diffraction dans ce cristal.
  29. Un métal dont l’espacement entre les plans est égal à 0,4164 nm diffracte les rayons X avec une longueur d’onde de 0,2879 nm. Quel est l’angle de diffraction pour le pic de diffraction de premier ordre ?
  30. L’or cristallise dans une cellule unitaire cubique à faces centrées. La réflexion de second ordre (n = 2) des rayons X pour les plans qui constituent les sommets et les fonds des cellules unitaires est à θ = 22,20°. La longueur d’onde des rayons X est de 1,54 Å. Quelle est la densité de l’or métallique ?
  31. Lorsqu’un électron d’un atome de molybdène excité passe de la couche L à la couche K, un rayon X est émis. Ces rayons X sont diffractés selon un angle de 7,75° par des plans dont la séparation est de 2,64 Å. Quelle est la différence d’énergie entre la coquille K et la coquille L dans le molybdène en supposant une diffraction de premier ordre?
Afficher les solutions choisies

1. La structure de cette forme de fer à basse température (inférieure à 910 °C) est cubique centrée sur le corps. Il y a un huitième atome à chacun des huit coins du cube et un atome au centre du cube.

3. Le nombre de coordination fait référence au nombre de voisins les plus proches. Un atome de chrome se trouve au centre d’un cube centré sur le corps et a huit voisins les plus proches (aux coins du cube) : quatre dans un plan au-dessus et quatre dans un plan au-dessous. Le nombre de coordination est donc de huit.

5. L’empaquetage le plus proche hexagonal se produit de telle sorte que chaque atome touche 12 voisins les plus proches : 6 dans sa propre couche et 3 dans chaque couche adjacente. Le nombre de coordination est donc de 12.

7. (a) Dans une cellule unitaire cubique centrée, les atomes de métal sont en contact le long de la diagonale intérieure du cube. La diagonale intérieure forme un triangle rectangle avec le bord de la cellule unitaire et la diagonale de la face. Utilisez le théorème de Pythagore pour déterminer la longueur de la diagonale, d, sur la face du cube en fonction du bord, e.

d2 = e2 + e2 = 2e2

d = \sqrt{2} e

La diagonale intérieure du cube est la longueur de quatre rayons atomiques et peut être calculée à nouveau en utilisant le théorème de Pythagore et la diagonale de la face et le bord.

\begin{array}{rll}\left(\text{diagonal}\right)^2&=&d^2+e^2 \\\\N &=& \left(\sqrt{2} e\right)+e^2 \N &=& 2e^2+e^2 \N &=&3e^2 \\\N- \N- &=&\sqrt{3}e=4r\end{array}

rayon de tungstène = \frac{\text{diagonal}}{4}=\frac{\sqrt{3}e}{4}=\frac{\sqrt{3}}{4}Gauche(3.165\mathring{\text{A}}\right)=1.370\mathring{\text{A}};

(b) Étant donné la structure cubique centrée, chaque cellule unitaire contient deux atomes. Utilisez la longueur du bord de la cellule unitaire pour calculer le volume de la cellule unitaire et le volume occupé par chaque atome. Multipliez pour obtenir le volume molaire et divisez la masse atomique par cette valeur pour obtenir la densité (e = longueur d’arête) :

V(cellule) = e3 = (3,165 \times 10-8 cm)3 = 3,170 \times 10-23 cm3

V(atome) = \frac{3,170\times {10}^{-23}{\text{cm}}^{3}{\text{2 atomes}=1.585\times {10}^{-23}{\text{cm}}^{3}{\text{atom}}^{-1}

V(mol) = 1.585 \times 10-23 cm3/atom \times 6.022 \times 1023 atomes/mol

= 9.546 cm3/mol

densité = \frac{183.85{\text{g mol}}^{-1}}{9.546{\text{cm}}^{3}{\text{mol}}^{-1}} = 19.26 g/cm

9. (a) Dans une cellule unitaire cubique centrée sur le corps, les atomes de métal sont en contact le long de la diagonale du cube. La diagonale du cube forme un triangle rectangle avec le bord de la cellule unitaire et la diagonale d’une face. Utilisez le théorème de Pythagore pour déterminer la longueur de la diagonale, d, sur la face du cube en fonction de e.

d2 = e2 + e2 = 2e2

d = \sqrt{2} e

La diagonale du cube est la longueur de quatre rayons atomiques et peut être calculée en utilisant à nouveau le théorème de Pythagore :

(diagonale)2 = (4r)2 = (2e)2 + e2 = 16r2 = 3e2

diagonale = 4r = \sqrt{3\text{e}}

r = \frac{\sqrt{3}}{4}\text{e}=\frac{\sqrt{3}}{4} (5.025 Å) = 2.176 Å;

(b) Étant donné une structure cubique centrée, chaque cellule unitaire contient deux atomes. Utilisez la longueur du bord de la cellule unitaire pour calculer le volume de la cellule unitaire et le volume occupé par chaque atome. Multipliez pour obtenir le volume molaire et divisez le poids atomique en grammes par cette valeur pour obtenir la densité (e = longueur d’arête):

V (cellule) = e3 = (5,025 \times 10-8 cm)3 = 1,26884 \times 10-22 cm3

V (atome) = 1.26884 \times \frac{10}^{-22}{\text{cm}}^{3}{\text{atom}}^{\text{-1}}{\text{2 atomes}} = 6.3442 \times 10-23 cm3

V (mole) = 6.3442 \times 10-23 cm3 \times 6.022 \times 1023 atomes/mol = 38.205 cm3

d(Ba) = \frac{137.33 g}{38.204 cm}^{3} = 3.595 g/cm3

11. La structure cristalline du Si montre qu’il est moins serré (numéro de coordination 4) dans le solide que l’Al (numéro de coordination 12).

13. Dans un réseau le plus étroitement empaqueté, deux trous tétraédriques existent pour chaque anion. Si seulement la moitié des trous tétraédriques sont occupés, les nombres d’anions et de cations sont égaux. La formule du sulfure de cadmium est CdS.

15. Dans un réseau d’ions d’oxyde le plus étroitement empaqueté, un trou octaédrique et deux trous tétraédriques existent pour chaque ion d’oxyde. Si la moitié des trous octaédriques sont remplis, il y a un ion Co pour deux ions oxyde. Si un huitième des trous tétraédriques est rempli, il y a un ion Co pour quatre ions oxyde. Pour chaque quatre ions oxyde, il y a deux ions Co dans les trous octaédriques et un Co dans un trou tétraédrique ; la formule est donc Co3O4.

17. Dans un réseau cubique simple, un seul trou cubique peut être occupé par un cation pour chaque anion du réseau. Le rapport entre le thallium et l’iodure doit être de 1:1 ; par conséquent, la formule du thallium est TlI.

19. Le rapport entre les trous octaédriques et les anions d’oxygène est de 1:1 dans un réseau le plus compact. Seulement la moitié des trous octaédriques sont occupés. Ainsi, le rapport titane/oxygène est de 1:2 et la formule est TiO2. Le pourcentage en masse de Ti dans la structure est :

pourcentage Ti = \frac{47,90}{47,90+\text{2(15,9994)}\times \text{100%}=\text{59,95%}

Le nombre d’oxydation du titane est +4 car il y a deux ions O2- pour chaque ion Ti.

21. Les deux ions ont une taille proche : Mg, 0,65 ; Li, 0,60. Cette similitude leur permet de s’échanger assez facilement. La différence de charge est généralement compensée par l’échange de Si4+ pour Al3+.

23. Le nombre total d’ions Mn est déterminé en additionnant les contributions des coins et du centre. Mn (coins) : 8 \times \frac{1}{8} ; Mn (centre) = 1. Contribution totale de Mn à la cellule unitaire = 2,

Pour O, il y a un total de 12 arêtes dans le cube et chaque ion dans l’arête contribue à un quart de la cellule unitaire. Par conséquent, il y a 12 \times \frac{1}{4} = 3 atomes d’oxygène. Le rapport est Mn:O = 2:3, et la formule est Mn2O3.

27. L’équation de Bragg est : nλ = 2d sin θ

où d est l’espacement entre les plans.

d = \frac{n{\lambda }}{\text{2 sin}\theta }=\frac{1(1.541 A)}{2\sin15.55^{\circ}}=\frac{1.541\mathring{\text{A}}{2(0.2681)} = 2.874 Å

29. \text{sin}\theta =\frac{n{\lambda }}{2d}=\frac{1)(0.2879\text{nm})}{(2)(0.4164)}=0.3457, donc θ = sin-1(0.3457) = 20.2°

31. Utilisez l’équation de Bragg, où n = 1,

λ = 2dsinθ =2(2.64 Å)sin 7.75 = 0.712 Å

Alors E=\frac{hc}{\lambda}=\frac{(6.626\times {10}^{-34}\text{J s})(2.998\times {10}^{8}{\text{m s}}^{-1})}{0.712\times {10}^{-10}\text{m}} =2.79\times {10}^{-15}\text{J}=1.74\times {10}^{4}\text{eV}

Glossary

Solide cubique centré (BCC) : structure cristalline qui possède une cellule unitaire cubique avec des points de réseau aux coins et au centre de la cellule

cellule unitaire cubique centrée : unité répétitive la plus simple d’un cristal cubique centré sur le corps ; c’est un cube contenant des points de réseau à chaque coin et au centre du cube

Équation de Bragg : équation qui relie les angles auxquels les rayons X sont diffractés par les atomes à l’intérieur d’un cristal

numéro de coordination : nombre d’atomes les plus proches de tout atome donné dans un cristal ou de l’atome métallique central dans un complexe

cubic closest packing (CCP) : structure cristalline dans laquelle des plans d’atomes ou d’ions étroitement emballés sont empilés comme une série de trois couches alternées d’orientations relatives différentes (ABC)

diffraction : redirection du rayonnement électromagnétique qui se produit lorsqu’il rencontre une barrière physique de dimensions appropriées

Solide cubique à faces centrées (FCC) : structure cristalline constituée d’une cellule unitaire cubique avec des points de réseau sur les coins et au centre de chaque face

cellule unitaire cubique à faces centrées : unité répétitive la plus simple d’un cristal cubique à faces centrées ; c’est un cube contenant des points de réseau à chaque coin et au centre de chaque face

hexagonal closest packing (HCP) : structure cristalline dans laquelle des couches serrées d’atomes ou d’ions sont empilées comme une série de deux couches alternées d’orientations relatives différentes (AB)

trou : (aussi, interstice) espace entre les atomes dans un cristal

isomorphe : possédant la même structure cristalline

trou octaédrique : espace ouvert dans un cristal au centre de six particules situées aux coins d’un octaèdre

cellule unitaire cubique simple : (aussi, cellule unitaire cubique primitive) cellule unitaire dans la structure cubique simple

simple cubic structure : structure cristalline avec une cellule unitaire cubique avec des points de treillis seulement aux coins

space treillis : tous les points dans un cristal qui ont des environnements identiques

trou tétraédrique : Espace tétraédrique formé par quatre atomes ou ions dans un cristal

cellule unitaire : plus petite portion d’un réseau spatial qui est répétée en trois dimensions pour former le réseau entier

Cristallographie aux rayons X : technique expérimentale pour déterminer les distances entre les atomes dans un cristal en mesurant les angles auxquels les rayons X sont diffractés lorsqu’ils traversent le cristal

.

Articles