À quoi servent les tableaux de caractères ?
À ce stade, une bonne question est : à quoi sert d’apprendre les tableaux de caractères ? La réponse simple est que la symétrie et la table de caractères associée d’une molécule peuvent être utilisées pour interpréter et prédire de nombreux aspects des spectroscopies chimiquement significatives ainsi que des liaisons. Nous allons illustrer ceci en nous concentrant sur les modes vibrationnels d’une molécule.
En laboratoire, nous pouvons recueillir des données expérimentales utiles en utilisant la spectroscopie infrarouge (IR) et Raman. Ces données peuvent être comparées au nombre de bandes actives IR et/ou Raman prédites à partir de l’application de la théorie des groupes et de la table de caractères correcte. Les mathématiques (théorie des groupes et algèbre matricielle) qui sous-tendent ce traitement servent de base théorique solide. Les manipulations décrites ci-dessous fonctionnent parce que toutes les opérations de symétrie d’une molécule constituent un groupe mathématique et obéissent aux règles de ce groupe. Comme indiqué précédemment, nous n’avons pas besoin de maîtriser ce domaine des mathématiques pour faire bon usage des tables de caractères.
Degrees of Freedom and Vibrations in Molecules
Ici, nous allons d’abord aborder les degrés de liberté pour une molécule simple (l’eau). Nous verrons très rapidement pourquoi il est très bénéfique d’employer la symétrie lors de l’étude de plus grandes molécules.
Pour une molécule avec « N » atomes, il y a 3N degrés de liberté (rappelez-vous que nous vivons dans un monde tridimensionnel de coordonnées x, y, z). Pour une molécule non linéaire, 3 degrés de liberté peuvent être signés à des translations – mouvement d’un corps dans son ensemble (Tx, Ty, Tz) et 3 à des rotations (Rx, Ry, Rz). Les autres mouvements des atomes sont des déplacements des atomes par rapport à leur position moyenne – le centre de gravité ne change pas. Ces vibrations fondamentales sont appelées « modes normaux ». Ainsi, une molécule non linéaire possède 3N-6 modes normaux. Pour l’eau, le nombre de modes normaux est de 3 (3 x 3 – 6 = 3). Pour les molécules linéaires, il y a 3N-5 modes normaux.
Pour l’eau, qui a bien sûr été intensivement étudiée, nous savons que les 3 vibrations sont les suivantes.
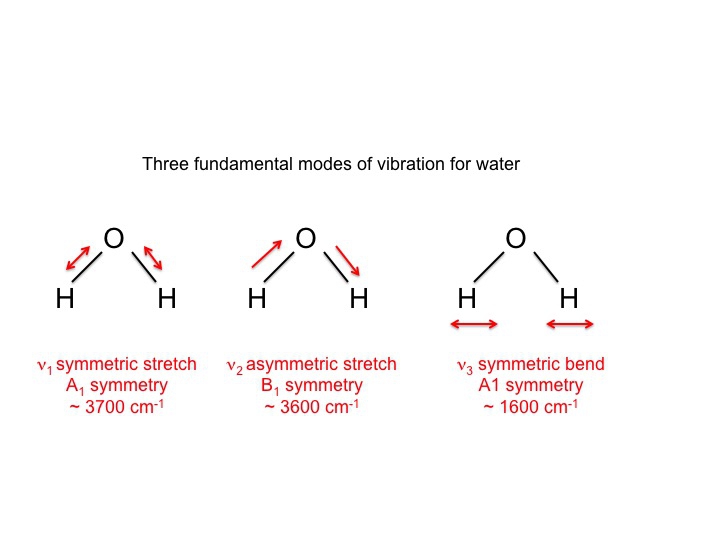
Les symboles utilisés pour décrire ces modes (A1, B1) sont les mêmes symboles Mulliken que nous avons rencontrés dans notre discussion sur les tables de caractères. En d’autres termes, les vibrations, qui sont des propriétés moléculaires, peuvent être décrites par des espèces de symétrie ou des représentations irréductibles. En fait, une grande partie de la littérature impliquant la spectroscopie vibrationnelle utilise ces symboles comme une façon abrégée de communiquer des informations.
Il devrait être assez évident que le nombre de vibrations augmente rapidement avec des augmentations même modestes du nombre d’atomes dans la molécule. Déterminer les types de vibrations par inspection (comme nous l’avons fait pour l’eau) devient maintenant beaucoup plus difficile. Par exemple, considérez les composés suivants :
H2O 3 atomes 3 vibrations
PH3 4 atomes 6 vibrations
CO22-. 4 atomes 6 vibrations
XeF4 5 atomes 9 vibrations
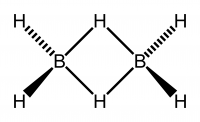
B2H6 8 atomes 18 vibrations
Pour le diborane (B2H6) qui a une symétrie D2h déterminer la nature et l’espèce de symétrie des 18 vibrations par inspection serait une tâche ardue. Cependant, armé de la table de caractères pour D2h et de la connaissance des propriétés de symétrie, la tâche de déterminer l’espèce de symétrie de toutes les vibrations est simple.
Pour le cas de l’eau, nous pourrions présenter la table de caractères (C2v) avec les 3 vibrations (ν1, v2, v3) énumérées dans la colonne des propriétés moléculaires comme indiqué ci-dessous. (ν = symbole grec « nu »)

Cependant, en général, cette approche est peu pratique. Prenons l’exemple de la pyridine (C5H5N). Le groupe ponctuel est également C2v mais la molécule compte 11 atomes. Le nombre de modes fondamentaux de vibration est de 27 ( 3 x 11 – 6 = 27).
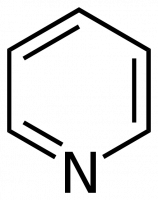
Dans ce cas, nous devrions établir un tableau de caractères C2v montrant les symétries des 27 vibrations. Pour cette raison, les vibrations ne sont normalement pas incluses dans les tables de caractères. Au lieu de cela, c’est à l’utilisateur (vous) de déterminer le nombre et le type de vibrations (telles que définies par leurs espèces de symétrie) pour toutes les molécules rencontrées. La façon dont nous procédons est décrite ci-dessous.
Représentations réductibles
Comme indiqué précédemment, une des propriétés importantes des tables de caractères est que les opérations de symétrie sont membres d’un groupe mathématique et que des relations importantes existent entre elles. En général, on peut dire la même chose des espèces de symétrie ou des représentations irréductibles des propriétés moléculaires. Les produits issus de la combinaison des caractères des représentations irréductibles, soit par multiplication, soit par addition/soustraction, obéissent également aux règles du groupe. Les nouvelles représentations ne sont plus les plus simples possibles et sont appelées « représentations réductibles » car elles peuvent être « réduites » jusqu’à leurs éléments constitutifs.
Par exemple, pour l’eau, les symétries des translations (Tx, Ty, Tz) peuvent être glanées directement dans la table de caractères C2v. Il s’agit de A1, B1 et B2. Nous pouvons représenter ces trois degrés de liberté par une représentation ΓT et nous pouvons écrire l’expression ci-dessous. (Γ = lettre grecque majuscule « gamma »).
ΓT = A1 + B1 + B2
Nous savons que A1, B1 et B2 ne sont que les notations abrégées des espèces de symétrie (représentations irréductibles). Nous pouvons donc simplement écrire les caractères de ΓT en additionnant les caractères individuels de A1, B1 et B2 de la table de caractères C2v.
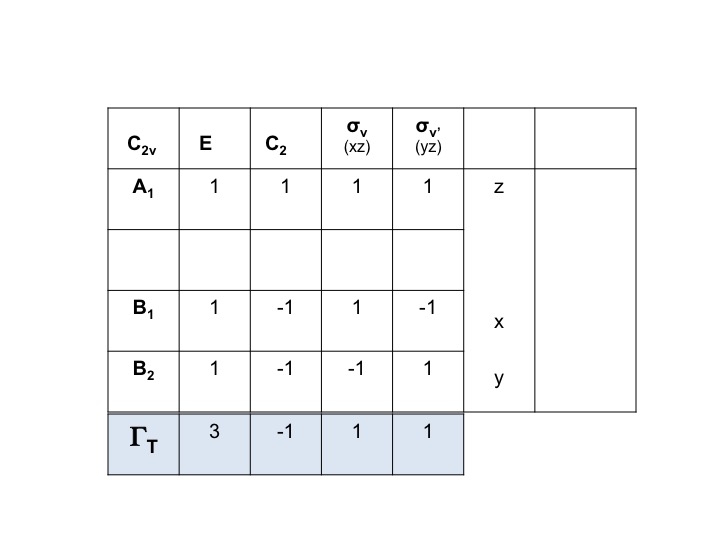
Donc ΓT = 3 -1 1 1.
C’est une représentation réductible valide et un membre du groupe C2v.
De la même manière, nous pouvons écrire la représentation réductible pour les trois rotations et toutes les vibrations.
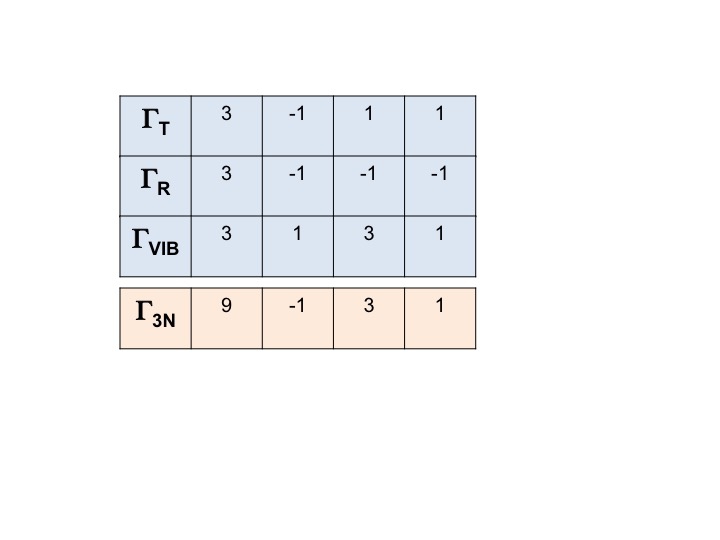
La représentation pour TOUS les degrés de liberté de la molécule (3N) peut être écrite comme
Γ3N = ΓT + ΓR + ΓVIB
et la représentation réductible pour celle-ci est obtenue en additionnant simplement les caractères pour ΓT, ΓR et ΓVIB.
Γ3N = 9 -1 3 1
Notez bien ceci – cela reviendra plus tard !
Bien que l’ensemble des caractères 9 -1 3 1 soit un membre valide du groupe C2v, il n’est pas particulièrement utile pour discuter des propriétés moléculaires. Ce qui est vraiment nécessaire est le langage des espèces de symétrie sténographique (symboles Mulliken, A1, B1 etc.). En d’autres termes, nous voulons exprimer Γ3N en termes de A1, B1, etc. A partir des informations couvertes ci-dessus, on peut facilement montrer par inspection que :
Γ3N = 3A1 +A2 + 3B1 +2B2
La bonne nouvelle est que pour d’autres molécules plus complexes, nous n’avons pas à effectuer cette tâche par inspection car :
1. Nous pouvons facilement générer Γ3N comme représentation réductible pour une molécule (si nous connaissons sa symétrie de groupe ponctuel).
2. Nous pouvons facilement convertir la représentation réductible de Γ3N en la somme de ses espèces de symétrie (symboles de Mulliken) en utilisant une formule « simple » connue comme la formule de réduction.
Méthode générale pour obtenir Γ3N
Étape 1
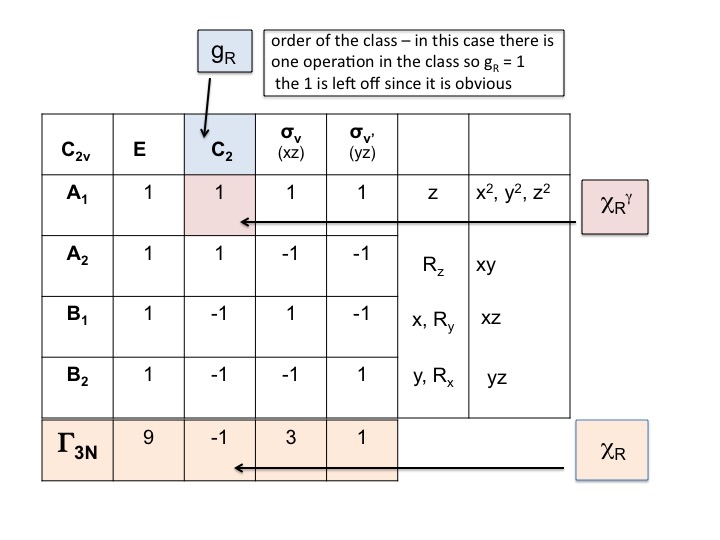
Prendre le tableau de caractères de la molécule et ajouter une ligne en bas. Dans cette ligne, générez la représentation réductible pour ΓT (ou Γxyz) comme nous l’avons fait ci-dessus, simplement en ajoutant les caractères pour chaque opération qui correspondent aux propriétés moléculaires pour x, y et z. Pour C2v, nous avons déjà montré que ce sont les caractères correspondant à A1, B1 et B2.
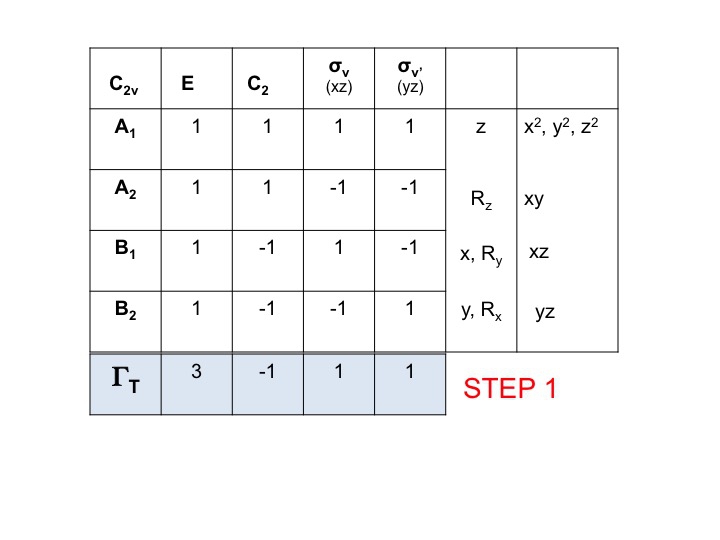
Étape 2
Ajouter une autre ligne sous ΓT et écrire le nombre d’atomes qui NE CHANGENT PAS leur emplacement pendant chaque opération de symétrie. C’est là que vous réalisez l’utilité d’un véritable ensemble de modèles moléculaires. Pour ce faire, vous devez également savoir où se trouvent les éléments de symétrie et comment les opérations de symétrie affectent la molécule. Bien entendu, vous savez déjà comment procéder puisque vous avez étudié la notation de Schönflies et que vous savez comment attribuer le groupe de points d’une molécule. Le tableau de caractères a également toutes les opérations de symétrie énumérées par classe le long de la ligne supérieure.
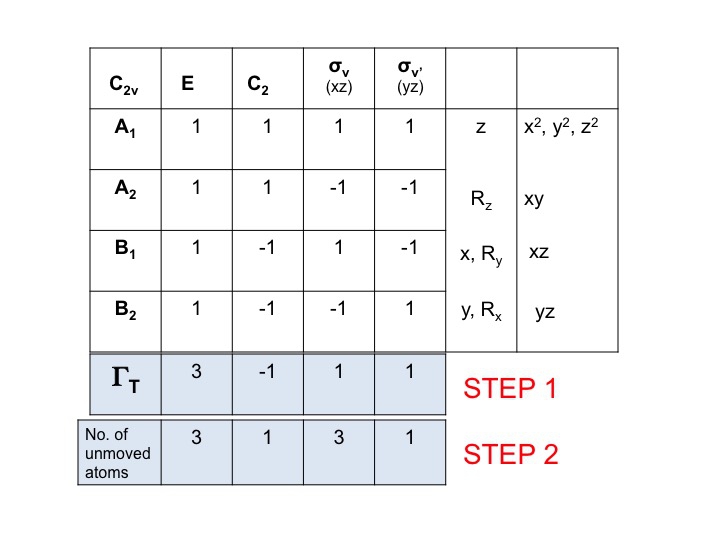
Ainsi, pour l’eau (3 atomes) sous E, il y a 3 atomes immobiles, mais pour C2, les deux H se déplacent mais comme l’atome O se trouve sur l’axe C2, il ne change pas d’emplacement et nous enregistrons donc 1 sous la colonne C2. Le nouvel ensemble de nombres généré à l’étape 2 (3 1 3 1) est également une représentation réductible en C2v et obéit aux règles du groupe.
Étape 3
Dans cette étape, nous multiplions simplement ensemble les caractères qui ont été générés aux étapes 1 et 2. Le résultat (troisième ligne) est la représentation réductible pour Γ3N (ou ΓTOT). C’est aussi simple que cela.
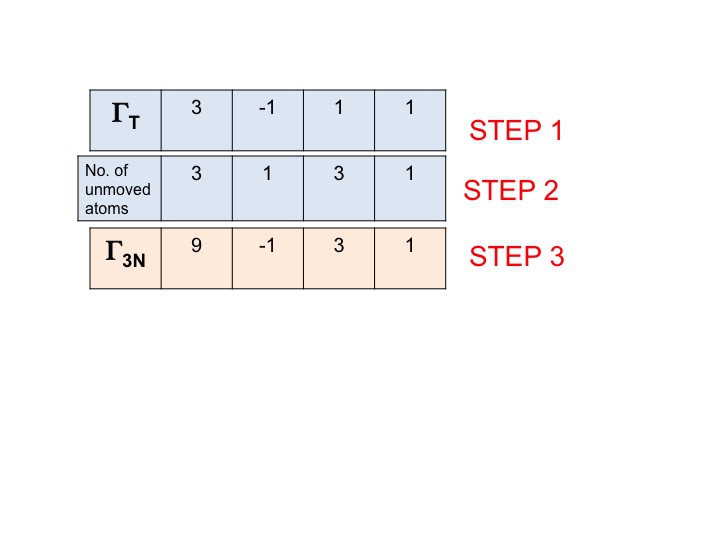
Vous noterez que la nouvelle représentation réductible (9 -1 1 3) est identique à la représentation pour Γ3N que nous avons obtenue précédemment par inspection.
Réduction de la représentation réductible
Pour convertir TOUTE représentation réductible en la somme de ses représentations irréductibles (espèces de symétrie ou symboles de Mulliken), nous utilisons une formule de réduction :

Vous pouvez facilement trouver cette information dans la table des caractères :
Revenons à notre exemple pour l’eau : Groupe ponctuel C2v, ordre (g) = 4
La représentation réductible pour Γ3N = 9 -1 3 1
Le nombre de fois où A1 apparaît dans cette représentation est donc
aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3
donc Γ3N contient 3 espèces à symétrie A1. Les nombres des autres espèces de symétrie sont calculés comme suit:
aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 1 A2 présent
aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 B1 présent
aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1} = 2 2 B2 présent
Nous pouvons maintenant écrire Γ3N = 3A1 + A2 + 3B1 + 2B2 (exactement ce que nous avons obtenu par « inspection » ci-dessus. Nous pouvons maintenant soustraire les espèces de symétrie pour les translations et les rotations et cela nous donnera le nombre et les espèces de symétrie des modes fondamentaux de vibration. ΓT et ΓR peuvent être obtenus directement à partir de la table des caractères.
Γ3N = 3A1 + A2 + 3B1 + 2B2
ΓT = A1 + B1 + B2
ΓR = A2 + B1 + B2
ΓVIB = Γ3N – ΓT – ΓR = 2A1 +B1
Donc les trois modes normaux de vibration pour l’eau ont les symétries A1, A1 et B1.
Nous avons maintenant une méthode générale pour déterminer tous les modes fondamentaux de vibration d’une molécule et exprimer ces modes dans le langage abrégé des symboles de Mulliken. C’est l’un des exercices sur lequel vous serez testé dans l’examen 1. La meilleure façon de devenir confiant avec cette méthode est de pratiquer autant d’exemples possibles que vous le pouvez !
Suivant : Règles de sélection