Less…
![]()
![]()
Pythagoraan kolmio on positiivisten kokonaislukujen ![]() ,
, ![]() ja
ja ![]() sellainen kolmio, että on olemassa suorakulmainen kolmio, jonka jalat ovat
sellainen kolmio, että on olemassa suorakulmainen kolmio, jonka jalat ovat ![]() ja hypotenuusa
ja hypotenuusa ![]() . Pythagoraan lauseen mukaan tämä vastaa sitä, että löydetään positiiviset kokonaisluvut
. Pythagoraan lauseen mukaan tämä vastaa sitä, että löydetään positiiviset kokonaisluvut ![]() ,
, ![]() ja
ja ![]() , jotka tyydyttävät
, jotka tyydyttävät
|
(1)
|
Pienin ja tunnetuin Pythagoraan kolmikko on ![]() . Suorakulmaista kolmiota, jolla on nämä sivupituudet, kutsutaan joskus 3,4,5-kolmioksi.
. Suorakulmaista kolmiota, jolla on nämä sivupituudet, kutsutaan joskus 3,4,5-kolmioksi.
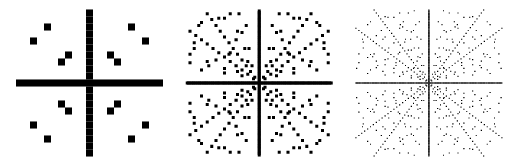
Yllä on esitetty peräkkäin suuremmille rajoille sellaisia pisteitä ![]() -tasossa, joiden
-tasossa, joiden ![]() on Pythagoraan kolmio. Nämä kuvaajat sisältävät
on Pythagoraan kolmio. Nämä kuvaajat sisältävät ![]() :n ja
:n ja ![]() :n negatiiviset arvot, joten ne ovat symmetrisiä sekä x- että y-akselien suhteen.
:n negatiiviset arvot, joten ne ovat symmetrisiä sekä x- että y-akselien suhteen.

Viitaten edellä on esitetty peräkkäin suuremmille rajoille kuvaajat pisteistä, jotka ovat ![]() -tasossa siten, että
-tasossa siten, että ![]() :ssä on pythagoraan kolmikko.
:ssä on pythagoraan kolmikko.

Tavanomaista on tarkastella vain primitiivisiä Pythagoraan kolmioita (joita kutsutaan myös ”pelkistetyiksi ”kolmioiksi), joissa ![]() ja
ja ![]() ovat suhteellisen alkulukuisia, koska muut ratkaisut voidaan tuottaa triviaalisti primitiivisistä. Alkeiskolmioita on havainnollistettu edellä, ja voidaan heti huomata, että alkuperäisen piirroksen imprimitiivisiä kolmioita vastaavat säteittäiset viivat puuttuvat tästä kuvasta. Alkeisratkaisuissa jommankumman
ovat suhteellisen alkulukuisia, koska muut ratkaisut voidaan tuottaa triviaalisti primitiivisistä. Alkeiskolmioita on havainnollistettu edellä, ja voidaan heti huomata, että alkuperäisen piirroksen imprimitiivisiä kolmioita vastaavat säteittäiset viivat puuttuvat tästä kuvasta. Alkeisratkaisuissa jommankumman ![]() :n tai
:n tai ![]() :n on oltava parillinen ja toisen pariton (Shanks 1993, s. 141), jolloin
:n on oltava parillinen ja toisen pariton (Shanks 1993, s. 141), jolloin ![]() on aina pariton.
on aina pariton.
Lisäksi jokaisen Pythagoraan kolmion yksi sivu on jaollinen kolmella, toinen neljällä ja kolmas viidellä. Yhdellä sivulla voi olla kaksi näistä jakajista, kuten (8, 15, 17), (7, 24, 25) ja (20, 21, 29), tai jopa kaikki kolme, kuten (11, 60, 61).
Edellyttäen alkukolmosta ![]() saadaan kolme uutta alkukolmosta
saadaan kolme uutta alkukolmosta
|
(2)
|
|||
| (a_2,b_2,b_3,c_3) |
(4)
|
missä
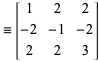 |
(5)
|
|
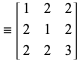 |
(6)
|
|
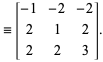 |
(7)
|
Hall (1970) ja Roberts (1977) todistavat, että ![]() on primitiivinen pythagoraaninen kolmikko, jos
on primitiivinen pythagoraaninen kolmikko, jos
|
(8)
|
jossa ![]() on matriisien
on matriisien ![]() ,
, ![]() ,
, ![]() äärellinen tuote. Tästä seuraa, että jokaisen primitiivisen Pythagoraan kolmion on oltava äärettömän joukon
äärellinen tuote. Tästä seuraa, että jokaisen primitiivisen Pythagoraan kolmion on oltava äärettömän joukon
 |
(9)
|
Pythagoras ja babylonialaiset antoivat kaavan (ei välttämättä alkukantaisten) kolmioiden tuottamiseksi seuraavasti
|
(10)
|
varten ![]() , joka tuottaa joukon erillisiä kolmosia, joka ei sisällä kaikkia primitiivisiä eikä kaikkia imprimitiivisiä kolmosia (ja jossa erikoistapauksessa
, joka tuottaa joukon erillisiä kolmosia, joka ei sisällä kaikkia primitiivisiä eikä kaikkia imprimitiivisiä kolmosia (ja jossa erikoistapauksessa ![]() ,
, ![]() ).
).
Varhaiset kreikkalaiset antoivat
|
(11)
|
jossa ![]() ja
ja ![]() ovat suhteellisesti alkulukuja ja vastakkaisia pariteetteja (Shanks 1993, s. 141), mikä synnyttää joukon erillisiä kolmosia, jotka sisältävät täsmälleen primitiiviset kolmoset (kun
ovat suhteellisesti alkulukuja ja vastakkaisia pariteetteja (Shanks 1993, s. 141), mikä synnyttää joukon erillisiä kolmosia, jotka sisältävät täsmälleen primitiiviset kolmoset (kun ![]() ja
ja ![]() on lajiteltu asianmukaisesti).
on lajiteltu asianmukaisesti).
Olkoon ![]() Fibonaccin luku. Silloin
Fibonaccin luku. Silloin
|
(12)
|
tuottaa erillisiä Pythagoraan kolmosia (Dujella 1995), vaikkakaan ei tyhjentävästi sen enempää primitiivisille kuin imprimitiivisillekin kolmosille. Yleisemmin, kun lähdetään liikkeelle positiivisista kokonaisluvuista ![]() ,
, ![]() ja rakennetaan Fibonaccin kaltainen sarja
ja rakennetaan Fibonaccin kaltainen sarja ![]() , jonka termit ovat
, jonka termit ovat ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , … tuottaa erillisiä Pythagoraan kolmosia
, … tuottaa erillisiä Pythagoraan kolmosia
|
(13)
|
(Horadam 1961), missä
|
(24)
|
(Beiler 1966, s. 116). Huomaa, että ![]() jos
jos ![]() on alkuluku tai kaksi kertaa alkuluku. Ensimmäiset luvut
on alkuluku tai kaksi kertaa alkuluku. Ensimmäiset luvut ![]() , 2, … ovat 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 4, 1, …. (OEIS A046079).
, 2, … ovat 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 4, 1, …. (OEIS A046079).
Että löydetään niiden tapojen lukumäärä ![]() , joilla luku
, joilla luku ![]() voi olla primitiivisen suorakulmaisen kolmion hypotenuusa, kirjoitetaan sen kertolasku seuraavasti
voi olla primitiivisen suorakulmaisen kolmion hypotenuusa, kirjoitetaan sen kertolasku seuraavasti
|
(25)
|
joissa ![]() s on muotoa
s on muotoa ![]() ja
ja ![]() s on muotoa
s on muotoa ![]() . Mahdollisten primitiivisten suorakulmaisten kolmioiden lukumäärä on tällöin
. Mahdollisten primitiivisten suorakulmaisten kolmioiden lukumäärä on tällöin
|
(26)
|
Esim, ![]() koska
koska
|
(27)
|
|||
|
(28)
|
Suureen ![]() arvot
arvot ![]() , 2, … ovat 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …. (OEIS A024362). Ensimmäiset alkuluvut muodossa
, 2, … ovat 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …. (OEIS A024362). Ensimmäiset alkuluvut muodossa ![]() ovat 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, …. (OEIS A002144), joten pienimmät sivupituudet, jotka ovat 1, 2, 4, 8, 16, … primitiivisten suorakulmaisten kolmioiden hypotenuusia, ovat 5, 65, 1105, 32045, 1185665, 48612265, …. (OEIS A006278).
ovat 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, …. (OEIS A002144), joten pienimmät sivupituudet, jotka ovat 1, 2, 4, 8, 16, … primitiivisten suorakulmaisten kolmioiden hypotenuusia, ovat 5, 65, 1105, 32045, 1185665, 48612265, …. (OEIS A006278).
Mahdollisten primitiivisten tai ei-primitiivisten suorakulmaisten kolmioiden, joiden hypotenuusa on ![]() , lukumäärä on
, lukumäärä on
|
(29)
|
|||
|
(30)
|
(korjataan kirjoitusvirhe Beiler 1966, p. 117, jossa sanotaan, että tämä kaava antaa vain ei-primitiivisten ratkaisujen lukumäärän), missä ![]() on neliösumman funktio. Esimerkiksi on olemassa neljä erillistä kokonaislukukolmiota, joiden hypotenuusa on 65, koska
on neliösumman funktio. Esimerkiksi on olemassa neljä erillistä kokonaislukukolmiota, joiden hypotenuusa on 65, koska
|
(31)
|
Ensimmäiset luvut ![]() , 2, … ovat 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, …. (OEIS A046080). Pienimmät hypotenuusat, joilla on
, 2, … ovat 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, …. (OEIS A046080). Pienimmät hypotenuusat, joilla on ![]() erillistä kolmikkoa, ovat 1, 5, 25, 125, 65, 3125, …. (OEIS A006339). Seuraavassa taulukossa esitetään hypotenuusat, joille on olemassa täsmälleen
erillistä kolmikkoa, ovat 1, 5, 25, 125, 65, 3125, …. (OEIS A006339). Seuraavassa taulukossa esitetään hypotenuusat, joille on olemassa täsmälleen ![]() erillistä suoraa kokonaislukukolmiota, kun
erillistä suoraa kokonaislukukolmiota, kun ![]() , 1, …, 5.
, 1, …, 5.
| OEIS | hypoteenit, joille on olemassa |
|
| 0 | A004144 | 1, 2, 3, 4, 6, 7, 7, 8, 8, 9, 11, 11, 12, 11, 12, 12, 12, 12, 14, 14, 16, 16, 18, … |
| 1 | A084645 | 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, … |
| 2 | A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, ….. |
| 3 | A084647 | 125, 250, 375, 500, 750, 875, 1000, 1125, 1375, … |
| 4 | A084648 | 65, 85, 130, 145, 170, 185, 195, 205, 221, 255, … |
| 5 | A084649 | 3125, 6250, 9375, 12500, 18750, 21875, 25000, … |
Siten niiden tapojen kokonaismäärä, joilla ![]() voi olla joko suorakulmaisen kolmion sääri tai hypotenuusa, on
voi olla joko suorakulmaisen kolmion sääri tai hypotenuusa, on
|
(32)
|
Muuttujan ![]() , 2, … arvot ovat 0, 0, 1, 1, 1, 2, 1, 1, 1, 2, 2, 2, 2, 2, 1, 4, 2, 2, 1, 5, 3, …. (OEIS A046081). Pienimmät luvut
, 2, … arvot ovat 0, 0, 1, 1, 1, 2, 1, 1, 1, 2, 2, 2, 2, 2, 1, 4, 2, 2, 1, 5, 3, …. (OEIS A046081). Pienimmät luvut ![]() , jotka voivat olla
, jotka voivat olla ![]() yleisen suorakulmaisen kolmion sivuja, kun
yleisen suorakulmaisen kolmion sivuja, kun ![]() , 2, … ovat 3, 5, 16, 12, 15, 125, 24, 40, …. (OEIS A006593; Beiler 1966, s. 114).
, 2, … ovat 3, 5, 16, 12, 15, 125, 24, 40, …. (OEIS A006593; Beiler 1966, s. 114).
On 50 Pythagoraan kolmikkoa, joiden hypotenuusa on pienempi kuin 100. Ensimmäiset niistä ovat kasvavan ![]() mukaan lajiteltuna (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084 ja A009000).
mukaan lajiteltuna (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084 ja A009000).
Näistä vain 16 on alkeiskolmioita, joiden hypotenuusa on pienempi kuin 100: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89) ja (65, 72, 97) (OEIS A046086, A046087 ja A020882).
Kirjoitetaan niiden kolmioiden lukumäärää, joiden hypotenuusa on ![]() ,
, ![]() , niiden kolmioiden lukumäärää, joiden hypotenuusa on
, niiden kolmioiden lukumäärää, joiden hypotenuusa on ![]() ,
, ![]() ja niiden alkeiskolmioiden lukumäärää, joiden hypotenuusa on pienempi kuin
ja niiden alkeiskolmioiden lukumäärää, joiden hypotenuusa on pienempi kuin ![]() ,
, ![]() . Seuraavassa taulukossa on sitten yhteenveto arvoista potensseille 10.
. Seuraavassa taulukossa on sitten yhteenveto arvoista potensseille 10.
| OEIS | |
|
| A101929 | 1, 50, 878, 12467, … | |
| A101930 | 2, 52, 881, 12471, ….. | |
| A101931 | 1, 16, 158, 1593, … |
Lehmer (1900) todisti, että sellaisten alkeisratkaisujen lukumäärä, joiden hypotenuusa on pienempi kuin ![]() , täyttää
, täyttää
|
(33)
|
(OEIS A086201).

Ensimmäisten alkukantaisten pythagoraanisten kolmioiden inradiukset kasvavalla järjestyksellä järjestettyinä ![]() ovat seuraavat: 1, 2, 2, 3, 3, 3, 3, 6, 6, 6, 5, 5, 4, 4, 10, … (OEIS A014498).
ovat seuraavat: 1, 2, 2, 3, 3, 3, 3, 6, 6, 6, 5, 5, 4, 4, 10, … (OEIS A014498).
On olemassa yleinen menetelmä, jolla saadaan Pythagoraan kolmioiden kolmikoita, joiden pinta-alat ovat yhtä suuret. Otetaan kolme generaattorijoukkoa seuraavasti
|
(34)
|
|||
|
(35)
|
|||
|
(36)
|
|||
|
(37)
|
|||
|
(38)
|
|||
|
(39)
|
Tällöin jokaisen kolmion (![]() ) on yhteinen pinta-ala
) on yhteinen pinta-ala
|
(40)
|
(Beiler 1966, pp. 126-127). Tämän funktion ainoa ääriarvo esiintyy kohdassa ![]() . Koska
. Koska ![]() on
on ![]() , pienin kolmen ei-primitiivisen suorakulmaisen kolmion jakama pinta-ala on
, pienin kolmen ei-primitiivisen suorakulmaisen kolmion jakama pinta-ala on ![]() , jolloin pinta-ala on 840 ja se vastaa kolmioita (24, 70, 74), (40, 42, 58) ja (15, 112, 113) (Beiler 1966, s. 126).
, jolloin pinta-ala on 840 ja se vastaa kolmioita (24, 70, 74), (40, 42, 58) ja (15, 112, 113) (Beiler 1966, s. 126).
Suorakulmaisia kolmioita, joiden pinta-ala koostuu yhdestä numerosta, ovat muun muassa ![]() (pinta-ala 6) ja
(pinta-ala 6) ja ![]() (pinta-ala 666666; Wells 1986, s. 89).
(pinta-ala 666666; Wells 1986, s. 89).
Fermat haastoi Mersennen vuonna 1643 etsimään pythagoraanisen kolmiyhteenvedon, jonka hypotenuusa ja jalkojen summa ovat neliöitä. Fermat löysi pienimmän tällaisen ratkaisun:
|
(41)
|
|||
|
(42)
|
|||
|
(43)
|
with
|
|
(44)
|
||
|
(45)
|
Seuraava ongelma on määrittää, voiko tietty kokonaisluku ![]() olla sellaisen suorakulmaisen kolmion pinta-ala, jolla on rationaaliset sivut. 1, 2, 3 ja 4 eivät ole minkään rationaalisivuisen suorakulmaisen kolmion pinta-aloja, mutta 5 on (3/2, 20/3, 41/6), samoin 6 (3, 4, 5). Tehtävän ratkaisuun liittyy elliptinen käyrä
olla sellaisen suorakulmaisen kolmion pinta-ala, jolla on rationaaliset sivut. 1, 2, 3 ja 4 eivät ole minkään rationaalisivuisen suorakulmaisen kolmion pinta-aloja, mutta 5 on (3/2, 20/3, 41/6), samoin 6 (3, 4, 5). Tehtävän ratkaisuun liittyy elliptinen käyrä
|
(46)
|
Ratkaisu (![]() ,
, ![]() ,
, ![]() ) on olemassa, jos (46) on rationaalinen ratkaisu, jolloin
) on olemassa, jos (46) on rationaalinen ratkaisu, jolloin
|
(47)
|
|||
|
(48)
|
(Koblitz 1993). Ei tunneta mitään yleistä menetelmää sen määrittämiseksi, onko ratkaisua mielivaltaiselle ![]() :lle, mutta J. Tunnellin vuonna 1983 kehittämän tekniikan avulla tietyt arvot voidaan sulkea pois (Cipra 1996).
:lle, mutta J. Tunnellin vuonna 1983 kehittämän tekniikan avulla tietyt arvot voidaan sulkea pois (Cipra 1996).