Seitsemännellätoista ja erityisesti kahdeksastoista vuosisadalla, sekä halusta ymmärtää luontoa että pyrkimyksestä valmistaa ilmapalloja, joilla he voisivat lentää (kuva 1), useat tiedemiehet selvittivät kaasujen makroskooppisten fysikaalisten ominaisuuksien eli paineen, tilavuuden, lämpötilan ja kaasun määrän väliset suhteet. Vaikka heidän mittauksensa eivät olleet nykypäivän mittapuulla tarkkoja, he pystyivät määrittämään näiden muuttujien parien (esim. paineen ja lämpötilan, paineen ja tilavuuden) väliset matemaattiset suhteet, jotka pätevät ideaalikaasulle – hypoteettiselle rakenteelle, jota todelliset kaasut lähestyvät tietyissä olosuhteissa. Lopulta nämä yksittäiset lait yhdistettiin yhdeksi yhtälöksi – ideaalikaasun laiksi – joka suhteuttaa kaasujen kaasumäärät toisiinsa ja on melko tarkka alhaisissa paineissa ja kohtalaisissa lämpötiloissa. Tarkastelemme yksittäisten suhteiden keskeistä kehitystä (pedagogisista syistä ei aivan historiallisessa järjestyksessä) ja kokoamme ne sitten yhteen ideaalikaasulakiin.

Kuva 1. Vuonna 1783 tapahtui ensimmäinen (a) vedyllä täytetyn ilmapallon lento, (b) miehitetty kuumailmapallolento ja (c) miehitetty vedyllä täytetyn ilmapallon lento. Kun kuvassa (a) esitetty vetytäytteinen ilmapallo laskeutui, Gonessen pelästyneet kyläläiset tuhosivat sen tiettävästi heittohaarukoilla ja veitsillä. Jälkimmäisen laukaisua katseli tiettävästi 400 000 ihmistä Pariisissa.

Paine ja lämpötila: Gay-Lussacin laki

Kuvittele, että täytät painemittariin kiinnitetyn jäykän säiliön kaasulla ja suljet säiliön niin, että kaasu ei pääse ulos. Jos astiaa jäähdytetään, sen sisällä oleva kaasu kylmenee niin ikään ja sen paineen havaitaan laskevan. Koska säiliö on jäykkä ja tiiviisti suljettu, sekä kaasun tilavuus että moolimäärä pysyvät vakiona. Jos palloa lämmitetään, sen sisällä oleva kaasu kuumenee (kuva 2) ja paine kasvaa.

Kuva 2. Lämpötilan vaikutus kaasun paineeseen: Kun lämpölevy on pois päältä, pallossa olevan kaasun paine on suhteellisen alhainen. Kun kaasua lämmitetään, kaasun paine pallossa kasvaa.

Tämä lämpötilan ja paineen välinen suhde havaitaan mille tahansa kaasunäytteelle, joka on suljettu vakiotilavuuteen. Kuvassa 3 on esimerkki kokeellisista paine-lämpötila-tiedoista ilmanäytteelle näissä olosuhteissa. Havaitaan, että lämpötila ja paine ovat lineaarisessa suhteessa toisiinsa, ja jos lämpötila on kelvinin asteikolla, niin P ja T ovat suoraan verrannollisia (jälleen kerran, kun tilavuus ja kaasumoolit pidetään vakioina); jos lämpötila kelvinin asteikolla nousee tietyllä kertoimella, kaasun paine nousee samalla kertoimella.

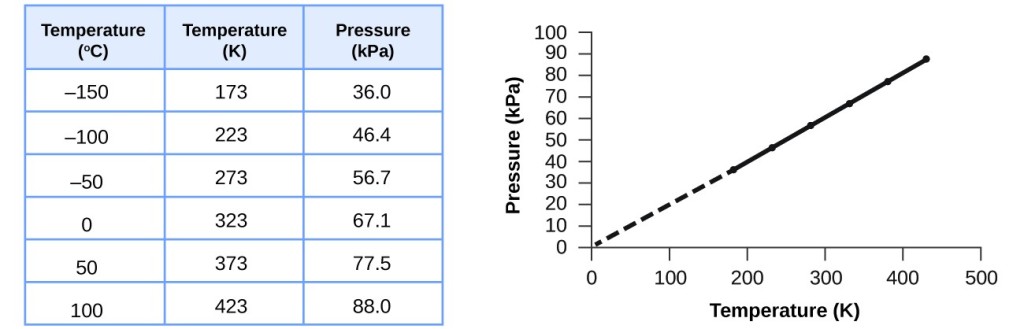
Kuva 3. Kun tilavuus ja ilmamäärä ovat vakiot, paine ja lämpötila ovat suoraan verrannollisia, jos lämpötila on kelvineissä. (Mittauksia ei voida tehdä alemmissa lämpötiloissa kaasun tiivistymisen vuoksi). Kun tämä viiva ekstrapoloidaan alempiin paineisiin, se saavuttaa paineen 0 -273 °C:ssa, joka on 0 kelvinin asteikolla ja alhaisin mahdollinen lämpötila, jota kutsutaan absoluuttiseksi nollapisteeksi.

Guillaume Amontons määritti ensimmäisenä empiirisesti kaasun paineen ja lämpötilan välisen suhteen (~1700), ja Joseph Louis Gay-Lussac määritteli suhteen tarkemmin (~1800). Tämän vuoksi kaasujen P-T-suhdetta kutsutaan joko Gay-Lussacin laiksi tai Amontonsin laiksi. Kummallakin nimellä se sanoo, että tietyn kaasumäärän paine on suoraan verrannollinen sen lämpötilaan kelvinin asteikolla, kun tilavuus pidetään vakiona. Matemaattisesti tämä voidaan kirjoittaa:

\large P\propto T

\large P=\text{constant}\times T

\large P=k\times T

missä ∝ tarkoittaa ”on verrannollinen”, ja k on suhteellisuusvakio, joka riippuu kaasun identiteetistä, määrästä ja tilavuudesta.

\large\frac{{P}_{1}}{{T}_{1}}=\frac{{{P}_{2}}{{{T}_{2}}

Tämä yhtälö on käyttökelpoinen paine-lämpötilalaskelmissa suljetulle kaasulle vakiotilavuudella. Huomaa, että lämpötilojen on oltava kelvinin asteikolla kaikissa kaasulakilaskelmissa (0 kelvinin asteikolla ja pienintä mahdollista lämpötilaa kutsutaan absoluuttiseksi nollapisteeksi). (Huomaa myös, että on ainakin kolme tapaa kuvata, miten kaasun paine muuttuu lämpötilan muuttuessa: Voimme käyttää arvotaulukkoa, kuvaajaa tai matemaattista yhtälöä.)

Tilavuus ja lämpötila: Charlesin laki

Jos täytämme ilmapallon ilmalla ja suljemme sen, ilmapallo sisältää tietyn määrän ilmaa ilmakehän paineessa, sanotaan 1 atm. Jos laitamme ilmapallon jääkaappiin, sen sisällä oleva kaasu kylmenee ja ilmapallo kutistuu (vaikka sekä kaasun määrä että sen paine pysyvät vakiona). Jos teemme ilmapallosta hyvin kylmän, se kutistuu paljon, ja lämmetessään se taas laajenee.

Nämä esimerkit lämpötilan vaikutuksesta tietyn määrän suljetun kaasun tilavuuteen vakiopaineessa pitävät yleisesti paikkansa: Tilavuus kasvaa lämpötilan noustessa ja pienenee lämpötilan laskiessa. Tilavuus-lämpötila-tiedot 1-molilliselle näytteelle metaanikaasua 1 atm:n lämpötilassa on lueteltu ja esitetty graafisesti kuvassa 4.

Kuva 4. Tilavuus ja lämpötila ovat lineaarisessa suhteessa toisiinsa 1 mooli metaanikaasua 1 atm:n vakiopaineessa. Jos lämpötila on kelvineissä, tilavuus ja lämpötila ovat suoraan verrannollisia. Suora pysähtyy 111 K:n lämpötilaan, koska metaani nesteytyy tässä lämpötilassa; ekstrapoloitaessa se leikkaa kuvaajan alkupisteen, joka edustaa absoluuttista nollalämpötilaa.

Tilavuuden ja lämpötilan välinen suhde tietyllä kaasumäärällä vakiopaineessa tunnetaan nimellä Kaarlen laki ranskalaisen tiedemiehen ja ilmapallolentojen uranuurtajan Jacques Alexandre César Kaarlen kunniaksi. Charlesin lain mukaan tietyn kaasumäärän tilavuus on suoraan verrannollinen sen lämpötilaan kelvinin asteikolla, kun paine pidetään vakiona.

Matemaattisesti tämä voidaan kirjoittaa seuraavasti:

\suuri V\propto T

\suuri V=\tekstivakio\cdot T

\suuri V=k\cdot T

k:n ollessa suhteellisuusvakio, joka riippuu kaasun määrästä ja paineesta.

\large\frac{{V}_{1}}{{T}_{1}}=\frac{{{V}_{2}}{{{T}_{2}}

Tilavuus ja paine: Boylen laki

Jos täytämme ilmatiiviisti suljetun ruiskun osittain ilmalla, ruiskussa on vakiolämpötilassa, vaikkapa 25 °C:n lämpötilassa, tietty määrä ilmaa. Jos työnnämme hitaasti mäntää sisään pitäen lämpötilan vakiona, ruiskussa oleva kaasu puristuu pienempään tilavuuteen ja sen paine kasvaa; jos vedämme mäntää ulos, tilavuus kasvaa ja paine pienenee. Tämä esimerkki tilavuuden vaikutuksesta tietyn määrän suljetun kaasun paineeseen pätee yleisesti. Suljetun kaasun tilavuuden pienentäminen kasvattaa sen painetta ja tilavuuden kasvattaminen pienentää sen painetta. Itse asiassa, jos tilavuus kasvaa tietyllä kertoimella, paine laskee samalla kertoimella ja päinvastoin. Huoneenlämpötilassa olevan ilmanäytteen tilavuus-paine-tiedot on esitetty graafisesti kuvassa 5.

Kuva 5. Kun kaasu vie pienemmän tilavuuden, sen paine on suurempi; kun se vie suuremman tilavuuden, sen paine on pienempi (olettaen, että kaasun määrä ja lämpötila eivät muutu). Koska P ja V ovat kääntäen verrannollisia, kuvaaja 1/P vs. V on lineaarinen.

Toisin kuin P-T- ja V-T-suhteet, paine ja tilavuus eivät ole suoraan verrannollisia toisiinsa. Sen sijaan P ja V ovat kääntäen verrannollisia: Paineen kasvattaminen johtaa kaasun tilavuuden pienenemiseen. Matemaattisesti tämä voidaan kirjoittaa:

\suuri P\propto 1\text{/}V\text{ tai }P=k\cdot 1\text{/}V\text{ tai }P\cdot V=k\text{ tai }{P}_{1}{V}_{1}={P}_{2}{V}_{2}

jossa k on vakio. Graafisesti tämä suhde näkyy suorana, joka saadaan, kun piirretään paineen \large\left(\frac{1}{P}\right) käänteisluku suhteessa tilavuuteen (V) tai tilavuuden \large\left(\frac{1}{V}\right) käänteisluku suhteessa paineeseen (V). Kaarevia viivoja sisältäviä kuvaajia on vaikea lukea tarkasti muuttujien pienillä tai suurilla arvoilla, ja niitä on vaikeampi käyttää teoreettisten yhtälöiden ja parametrien sovittamisessa kokeellisiin tietoihin. Näistä syistä tutkijat yrittävät usein löytää keinon ”linearisoida” datansa. Jos kuvaamme P:n ja V:n suhteen, saamme hyperbelin (ks. kuva 6).

Englantilainen luonnonfilosofi Robert Boyle julkaisi ensimmäisen kerran yli 300 vuotta sitten tietyn kaasumäärän tilavuuden ja paineen välisen suhteen vakiolämpötilassa. Se on tiivistetty lausumaan, joka tunnetaan nykyään Boylen lakina: Tietyn, vakiolämpötilassa pidetyn kaasumäärän tilavuus on kääntäen verrannollinen paineeseen, jossa se mitataan.

Chemistry in Action: Hengitys ja Boylen laki

Mitä teet noin 20 kertaa minuutissa koko elämäsi ajan taukoamatta ja usein jopa tiedostamatta sitä? Vastaus on tietenkin hengitys eli hengittäminen. Miten se toimii? Kävi ilmi, että kaasulakeja sovelletaan tähän. Keuhkot ottavat sisäänsä elimistön tarvitsemaa kaasua (happea) ja poistavat hukkakaasua (hiilidioksidia). Keuhkot koostuvat sienimäisestä, venyvästä kudoksesta, joka laajenee ja supistuu hengityksen aikana. Kun hengität sisään, pallea ja rintalihakset (kylkiluiden väliset lihakset) supistuvat, jolloin rintaontelo laajenee ja keuhkotilavuus kasvaa. Tilavuuden kasvu johtaa paineen alenemiseen (Boylen laki). Tämä saa ilman virtaamaan keuhkoihin (korkeasta paineesta matalaan paineeseen). Kun hengität ulos, prosessi kääntyy päinvastaiseksi: Pallea ja kylkilihakset rentoutuvat, rintaontelo supistuu ja keuhkojen tilavuus pienenee, jolloin paine kasvaa (Boylen laki jälleen) ja ilma virtaa ulos keuhkoista (korkeasta paineesta matalaan paineeseen). Tämän jälkeen hengität sisään ja ulos uudestaan ja uudestaan, ja toistat tätä Boylen lain sykliä koko loppuelämäsi ajan (kuva 7).

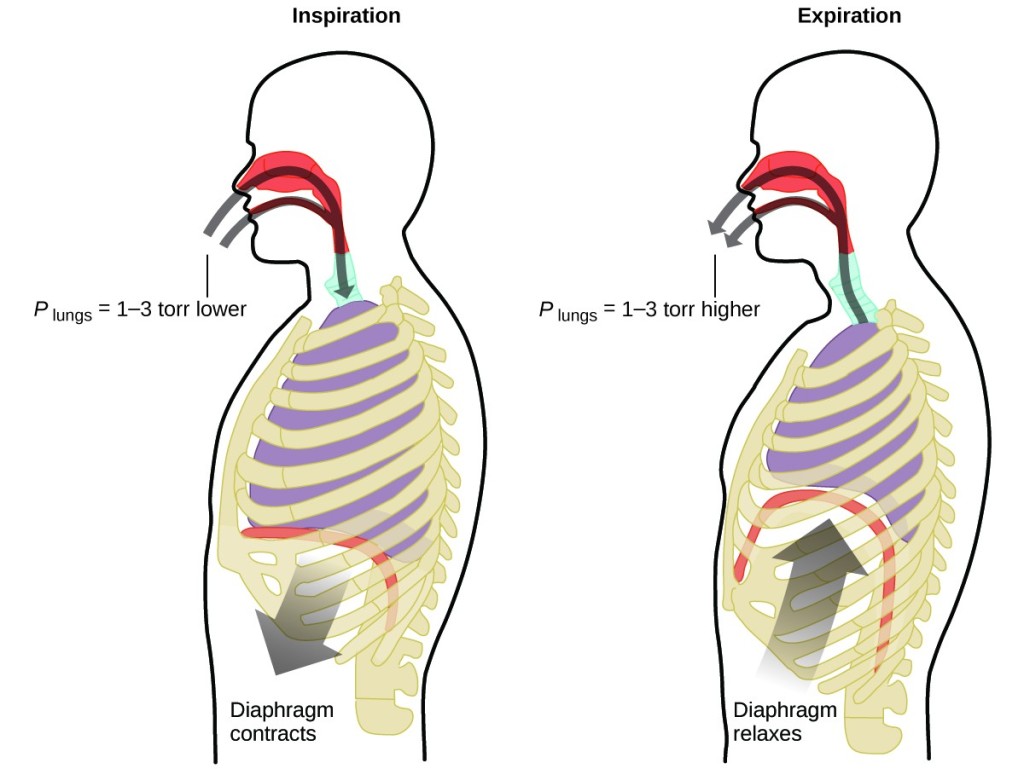
Kuva 7. Hengitys tapahtuu, koska keuhkojen tilavuuden laajeneminen ja supistuminen synnyttää pieniä paine-eroja keuhkojesi ja ympäristösi välille, jolloin ilmaa imetään keuhkoihin ja pakotetaan ulos keuhkoista.

Gasimoolit ja tilavuus: Avogadron laki

Italialainen tiedemies Amedeo Avogadro esitti vuonna 1811 hypoteesin kaasujen käyttäytymisen selittämiseksi, jonka mukaan kaikkien kaasujen yhtäläiset tilavuudet, mitattuna samoissa lämpötila- ja paineolosuhteissa, sisältävät saman määrän molekyylejä. Ajan mittaan tämä suhde sai tukea monista kokeellisista havainnoista, jotka ilmaistiin Avogadron lailla: Rajoitetun kaasun tilavuus (V) ja moolimäärä (n) ovat suoraan verrannollisia, jos paine ja lämpötila pysyvät vakiona.

Yhtälömuodossa tämä kirjoitetaan seuraavasti:

\large\begin{array}{ccccc}V\propto n& \text{or}& V=k\times n& \text{or}& \frac{{V}_{1}}{{n}_{1}}=\frac{{V}_{2}}{{n}_{2}}\end{array}

Matemaattiset suhteet voidaan määrittää myös muille muuttujapareille, kuten P vs. n ja n vs. T.

Sanasto

absoluuttinen nollapiste: Lämpötila, jossa kaasun tilavuus olisi nolla Charlesin lain mukaan.

Avogadron laki: kaasun tilavuus vakiolämpötilassa ja -paineessa on verrannollinen kaasumolekyylien lukumäärään

Boylen laki: vakiolämpötilassa pidetyn tietyn moolimäärän kaasun tilavuus on kääntäen verrannollinen paineeseen, jossa se mitataan

Charlesin laki:

Gay-Lussacin laki: tietyn moolimäärän kaasun tilavuus on suoraan verrannollinen sen kelvinilämpötilaan, kun paine pidetään vakiona

Gay-Lussacin laki: (myös Amontonin laki) tietyn moolimäärän kaasun paine on suoraan verrannollinen sen kelvinin lämpötilaan, kun tilavuus pidetään vakiona