Yli 90 % luonnossa esiintyvistä ja ihmisen valmistamista kiinteistä aineista on kiteisiä. Useimmat kiinteät aineet muodostuvat siten, että niiden hiukkaset ovat säännöllisessä järjestyksessä, koska hiukkasten väliset vetovoimaiset vuorovaikutukset maksimoituvat ja molekyylien välinen kokonaisenergia minimoituu, kun hiukkaset pakkautuvat tehokkaimmalla tavalla. Säännöllinen järjestely atomitasolla heijastuu usein makroskooppisella tasolla. Tässä moduulissa tutustumme joihinkin yksityiskohtiin metallisten ja ionisten kiteisten kiinteiden aineiden rakenteista ja opimme, miten nämä rakenteet määritetään kokeellisesti.

Metallien rakenteet

Aloitamme keskustelun kiteisistä kiinteistä aineista tarkastelemalla alkuainemetalleja, jotka ovat suhteellisen yksinkertaisia, koska kukin niistä sisältää vain yhdenlaista atomia. Puhdas metalli on kiteinen kiinteä aine, jossa metalliatomit on pakattu tiiviisti yhteen toistuvaan kuvioon. Jotkin metallien yleisistä ominaisuuksista, kuten muovattavuus ja sitkeys, johtuvat suurelta osin siitä, että samanlaiset atomit on järjestetty säännölliseen kuvioon. Metallien erilaiset ominaisuudet toiseen verrattuna riippuvat osittain niiden atomien koosta ja niiden tilajärjestelyjen erityispiirteistä. Seuraavissa kappaleissa tarkastelemme neljän yleisimmän metallien kiderakenteen yhtäläisyyksiä ja eroja.

Metallien yksikkösolut

Kiteisen kiinteän aineen, oli se sitten metalli tai ei, rakennetta kuvataan parhaiten tarkastelemalla sen yksinkertaisinta toistuvaa yksikköä, jota kutsutaan sen yksikköselloksi. Yksikkösolu koostuu hilapisteistä, jotka edustavat atomien tai ionien sijainteja. Koko rakenne koostuu sitten tästä kolmiulotteisesti toistuvasta yksikkösolusta, kuten kuvassa 1 on esitetty.

Kuva 1. Yksikkösolussa näkyy kaikissa suunnissa toistuvien ristikkopisteiden sijainnit.

Aloitetaan kiteiden ristikkorakenteen ja yksikkösolujen tutkiminen yksinkertaisimmasta rakenteesta ja yksinkertaisimmasta yksikkösolusta. Tämän havainnollistamiseksi kuvitellaan, että otetaan suuri määrä samanlaisia palloja, kuten tennispalloja, ja järjestetään ne tasaisesti astiaan. Yksinkertaisin tapa tehdä tämä olisi tehdä kerroksia, joissa yhden kerroksen pallot ovat suoraan alemman kerroksen pallojen yläpuolella, kuten kuvassa 2 on esitetty. Tätä järjestelyä kutsutaan yksinkertaiseksi kuutiorakenteeksi, ja yksikkösolua kutsutaan yksinkertaiseksi kuutiolliseksi yksikkösoluksi tai primitiiviseksi kuutiolliseksi yksikkösoluksi.

Kuva 2. Kun metalliatomit on järjestetty siten, että yhden kerroksen pallot ovat suoraan toisen kerroksen pallojen ylä- tai alapuolella, ristikkorakennetta kutsutaan yksinkertaiseksi kuutiorakenteeksi. Huomaa, että pallot ovat kosketuksissa.

Yksinkertaisessa kuutiorakenteessa pallot eivät ole pakattu niin tiiviisti kuin ne voisivat olla, ja ne ”täyttävät” vain noin 52 % säiliön tilavuudesta. Tämä on suhteellisen tehoton järjestely, ja vain yksi metalli (polonium, Po) kiteytyy yksinkertaiseen kuutiorakenteeseen. Kuten kuvassa 3 on esitetty, kiinteä aine, jossa on tämäntyyppinen järjestely, koostuu tasoista (tai kerroksista), joissa kukin atomi koskettaa vain neljää lähintä naapuria omassa kerroksessaan, yhtä atomia suoraan sen yläpuolella olevassa kerroksessa ja yhtä atomia suoraan sen alapuolella olevassa kerroksessa. Kiteisen kiinteän aineen kunkin hiukkasen kosketuksissa olevien muiden hiukkasten lukumäärää kutsutaan sen koordinaatioluvuksi. Yksinkertaisessa kuutiomassa olevan poloniumatomin koordinaatioluku on siis kuusi.

Kuva 3. Yksinkertaisen kuutioverkkorakenteen atomi koskettaa kuutta muuta atomia, joten sen koordinaatioluku on kuusi.

Yksikkösolu, joka toistuu kaikissa suunnissa, on yksinkertaisessa kuutioverkossa kahdeksan atomin keskipisteiden määrittämä kuutio, kuten kuvassa 4 on esitetty. Tämän yksikkösolun vierekkäisissä kulmissa olevat atomit ovat kosketuksissa toisiinsa, joten tämän solun reunan pituus on yhtä suuri kuin kaksi atomin sädettä eli yksi atomin halkaisija. Kuutioyksikkösolu sisältää vain niiden atomien osat, jotka ovat sen sisällä. Koska yksinkertaisen kuutiollisen yksikkösolun kulmassa oleva atomi sisältyy yhteensä kahdeksaan yksikkösoluun, vain yksi kahdeksasosa kyseisestä atomista on tietyn yksikkösolun sisällä. Ja koska jokaisessa yksinkertaisessa kuutiollisessa yksikkösolussa on yksi atomi jokaisessa sen kahdeksassa ”kulmassa”, yhden yksinkertaisen kuutiollisen yksikkösolun sisällä on 8 \times \frac{1}{8}=1 atomi.

Kuva 4. Yksinkertainen kuutioristikon yksikkösolu sisältää kahdeksasosan atomista jokaisessa kahdeksassa kulmassaan, joten se sisältää yhteensä yhden atomin.

Esimerkki 1: Metallien atomisäteen ja tiheyden laskeminen, osa 1

Alfa-poloniumin yksikkösolun reunan pituus on 336 pm.

1. Määritä poloniumatomin säde.
2. Määritä alfapoloniumin tiheys.

Näytä ratkaisu

Alfapolonium kiteytyy yksinkertaiseen kuutiomuotoiseen yksikkösoluun:

1. Kaksi vierekkäistä Poatomia koskettaa toisiaan, joten tämän solun reunan pituus on yhtä suuri kuin kaksi Poatomin sädettä: l=2r. Po:n säde on siis r=\dfrac{\text{l}}{2}=\dfrac{\text{336 pm}}{2}=\text{168 pm}.
2. Tiheys saadaan kaavalla \text{density}=\dfrac{\text{mass}}{\text{volume}}. Poloniumin tiheys voidaan määrittää määrittämällä sen yksikkösolun tiheys (yksikkösolun sisältämä massa jaettuna yksikkösolun tilavuudella). Koska Po:n yksikkösolu sisältää jokaisessa kahdeksassa kulmassaan yhden kahdeksasosan Po:n atomista, yksikkösolu sisältää yhden Po:n atomin.

Po:n yksikkösolun massa saadaan:

\text{1 Po:n yksikkösolu}\times \dfrac{\text{1 Po:n atomi}{\text{1 Po:n yksikkösolu}}\times \dfrac{\text{1 mol Po:n atomia}{6.022\times {10}^{23}\text{Po-atomit}}\times \dfrac{208.998\text{g}}{\text{1 mol Po}}=3.47\times {10}^{-22}\text{g}

Po-yksikkösolun tilavuus saadaan:

V={l}^{3}={(336\times {10}^{-10}\text{cm})}^{3}=3.79\times {10}^{-23}{\text{cm}}^{3}

(Huomaa, että reunan pituus muunnettiin pm:stä cm:ksi, jotta tiheydelle saatiin tavanomaiset tilavuusyksiköt.)

Siten tiheys \text{Po}=\dfrac{3.471\times {10}^{-22}\text{g}}{3.79\times {10}^{-23}{\text{cm}}^{3}}={\text{9.16 g/cm}}^{3}

Tarkista oppimisesi

Nikkelin yksikkösolun reunapituus on 0.3524 nm. Ni-hiukkasen tiheys on 8,90 g/cm3. Kiteytyykö nikkeli yksinkertaiseen kuutiorakenteeseen? Selitä.

Näytä ratkaisu

Ei. Jos Ni olisi yksinkertaisen kuutiomainen, sen tiheys olisi:

\text{1 Ni atomi}\times \dfrac{\text{1 mol Ni}}{6.022\times {10}^{23}\text{Ni-atomit}}\times \dfrac{58.693\text{g}}{\text{1 mol Ni}}=9.746\times {10}^{-23}\text{g}
V={l}^{3}={(3.524\times {10}^{-8}\text{cm})}^{3}=4.376\times {10}^{-23}{\text{cm}}^{3}

Tällöin Ni:n tiheys olisi =\dfrac{9.746\times {10}^{-23}\text{g}}{4.376\times {10}^{-23}{\text{cm}}^{3}}={\text{2.23 g/cm}}^{3}

Koska Ni:n todellinen tiheys ei ole lähelläkään tätä, Ni ei muodosta yksinkertaista kuutiorakennetta.

Useimmissa metallikiteissä on jokin neljästä suuresta yksikkösolutyypistä. Keskitymme nyt kolmeen kuutiomuotoiseen yksikkösoluun: yksinkertaiseen kuutiomuotoiseen (jonka olemme jo nähneet), kappalekeskeiseen kuutiomuotoiseen yksikkösoluun ja kasvokeskeiseen kuutiomuotoiseen yksikkösoluun, jotka kaikki on havainnollistettu kuvassa 5. (Huomaa, että itse asiassa on olemassa seitsemän erilaista hilajärjestelmää, joista joissakin on useampi kuin yksi hilatyyppi, eli kaikkiaan 14 erilaista yksikkösolutyyppiä. Jätämme monimutkaisemmat geometriat myöhemmäksi tässä moduulissa.)

Kuva 5. Metallien kuutiomaiset yksikkösolut osoittavat (ylemmissä kuvissa) ristikkopisteiden sijainnit ja (alemmissa kuvissa) yksikkösolussa sijaitsevat metalliatomit.

Jotkut metallit kiteytyvät järjestelyssä, jossa on kuutiomainen yksikkösolu, jonka kaikissa kulmissa on atomeja ja keskellä on atomi, kuten kuvassa 6. Tätä kutsutaan kappalekeskeiseksi kuutioksi (BCC, body-centered cubic). BCC-yksikkösolun kulmissa olevat atomit eivät ole kosketuksissa toisiinsa vaan keskellä olevaan atomiin. BCC-yksikkösolu sisältää kaksi atomia: kahdeksasosa atomista jokaisessa kahdeksassa kulmassa ( 8\times \frac{1}{8}=1 atomi kulmista) sekä yksi atomi keskeltä. Jokainen atomi tässä rakenteessa koskettaa neljää atomia sen yläpuolella olevassa kerroksessa ja neljää atomia sen alapuolella olevassa kerroksessa. Näin ollen BCC-rakenteen atomilla on koordinaatioluku kahdeksan.

Kuvio 6. Kuution ulkopuolisten molekyylien osat. Kappaleenkeskeisessä kuutiorakenteessa tietyn kerroksen atomit eivät kosketa toisiaan. Jokainen atomi koskettaa neljää atomia sen yläpuolella olevassa kerroksessa ja neljää atomia sen alapuolella olevassa kerroksessa.

BCC-järjestelyissä atomit ovat paljon tehokkaammin pakattuja kuin yksinkertaisessa kuutiorakenteessa, sillä ne vievät noin 68 % kokonaistilavuudesta. BCC-rakenteen omaavia isomorfisia metalleja ovat K, Ba, Cr, Mo, W ja Fe huoneenlämmössä. (Alkuaineita tai yhdisteitä, jotka kiteytyvät samalla rakenteella, sanotaan isomorfisiksi.)

Monet muut metallit, kuten alumiini, kupari ja lyijy, kiteytyvät järjestelyyn, jossa on kuutiomainen yksikkösolu, jossa on atomeja kaikissa kulmissa ja jokaisen sivun keskipisteissä, kuten kuvassa 7 on esitetty. Tätä järjestelyä kutsutaan kasvokeskittyneeksi kuutioksi (FCC). FCC-yksikkösolu sisältää neljä atomia: kahdeksasosa atomista jokaisessa kahdeksassa kulmassa ( 8 \ kertaa \frac{1}{8}=1 atomi kulmista) ja puolet atomista jokaisella kuudella pinnalla (6 \ kertaa \frac{1}{2}=3 atomia pinnoista). Kulmissa olevat atomit koskettavat viereisten kasvojen keskipisteissä olevia atomeja kuution kasvojen lävistäjiä pitkin. Koska atomit ovat identtisissä ristikkopisteissä, niillä on identtiset ympäristöt.

Kuvio 7. Kuution ulkopuolella olevat harmaat molekyylit. Kylkikeskittyneessä kuutiomaisessa kiinteässä aineessa on atomeja sen yksikkösolujen kulmissa ja, kuten nimikin kertoo, niiden kasvojen keskipisteissä.

FCC-järjestelyn atomit ovat pakkautuneet mahdollisimman tiiviisti toisiinsa, ja atomien osuus tilavuudesta on 74 %. Tätä rakennetta kutsutaan myös nimellä cubic closest packing (CCP). CCP:ssä on kolme toistuvaa kerrosta kuusikulmaisesti järjestettyjä atomeja. Kukin atomi koskettaa kuutta atomia omassa kerroksessaan, kolmea yläpuolella olevassa kerroksessa ja kolmea alapuolella olevassa kerroksessa. Tässä järjestelyssä jokainen atomi koskettaa 12 lähinaapuria, joten sen koordinaatioluku on 12. Se, että FCC- ja CCP-asetelmat ovat ekvivalentteja, ei ehkä ole heti selvää, mutta miksi ne ovat itse asiassa sama rakenne, on havainnollistettu kuvassa 8.

Kuva 8. CCP-järjestely koostuu kolmesta toistuvasta kerroksesta (ABCABC…), jotka koostuvat kuusikulmaisesti järjestetyistä atomeista. CCP-rakenteen atomeilla on koordinaatioluku 12, koska ne ovat yhteydessä kuuteen atomiin omassa kerroksessaan sekä kolmeen atomiin yläpuolella olevassa kerroksessa ja kolmeen atomiin alapuolella olevassa kerroksessa. Kääntämällä perspektiiviä voimme nähdä, että CCP-rakenteessa on yksikkösolu, jonka pinta sisältää kerroksen A atomin yhdessä kulmassa, kerroksen B atomeja diagonaalin poikki (kahdessa kulmassa ja keskellä pintaa) ja kerroksen C atomin jäljellä olevassa kulmassa. Tämä on sama kuin kasvokeskitetty kuutiomainen järjestely.

Koska tiiviimpi pakkautuminen maksimoi atomien välisen vetovoiman ja minimoi molekyylien välisen kokonaisenergian, useimpien metallien atomit pakkautuvat tällä tavalla. Yksinkertaisissa metallisissa kiderakenteissa esiintyy kahdenlaista tiiviimpää pakkautumista: CCP, johon olemme jo törmänneet, ja heksagonaalinen lähipakkaus (HCP), joka on esitetty kuvassa 9. Molemmat koostuvat heksagonaalisesti järjestäytyneiden atomien toistuvista kerroksista. Molemmissa pakkaustyypeissä toinen kerros (B) on sijoitettu ensimmäisen kerroksen (A) päälle siten, että jokainen toisen kerroksen atomi on kosketuksissa kolmen ensimmäisen kerroksen atomin kanssa. Kolmas kerros sijoitetaan kahdella tavalla. HCP:ssä kolmannen kerroksen atomit ovat suoraan ensimmäisen kerroksen atomien yläpuolella (eli kolmas kerros on myös tyypin A), ja pinoaminen koostuu vuorotellen tyypin A ja tyypin B tiiviisti pakatuista kerroksista (eli ABABAB⋯). CCP:ssä kolmannen kerroksen atomit eivät ole kummassakaan kahdessa ensimmäisessä kerroksessa olevien atomien yläpuolella (eli kolmas kerros on tyyppiä C), ja pinoaminen koostuu vuorotellen A-, B- ja C-tyypin tiiviisti pakatuista kerroksista (eli ABCABCABCABC⋯). Noin kaksi kolmasosaa kaikista metalleista kiteytyy tiiviimmin pinottuihin kerroksiin, joiden koordinaatioluvut ovat 12. HCP-rakenteeseen kiteytyviä metalleja ovat muun muassa Cd, Co, Li, Mg, Na ja Zn, ja CCP-rakenteeseen kiteytyviä metalleja ovat muun muassa Ag, Al, Ca, Cu, Ni, Pb ja Pt.

Kuva 9. Molemmissa lähipakkaustyypeissä atomit on pakattu mahdollisimman tiiviisti. Heksagonaalinen lähipakkaus koostuu kahdesta vuorottelevasta kerroksesta (ABABABAB…). Kuutionmuotoinen lähipakkaus koostuu kolmesta vuorottelevasta kerroksesta (ABCABCABC…).

Esimerkki 2: Metallien atomisäteen ja tiheyden laskeminen, osa 2

Kalsium kiteytyy kasvokeskiseen kuutiorakenteeseen. Sen yksikkösolun reunan pituus on 558,8 pm.

1. Mikä on Ca:n atomisäde tässä rakenteessa?
2. Laskekaa Ca:n tiheys.

Näytä ratkaisu

Osa 1

FCC-rakenteessa Ca-atomit ovat kosketuksissa toisiinsa poikkileikkauspinnan diagonaalilla, joten diagonaalin pituus on yhtä suuri kuin neljä Ca-atomin sädettä (d = 4r). Kaksi vierekkäistä reunaa ja pinnan lävistäjä muodostavat suorakulmaisen kolmion, jonka jokaisen sivun pituus on 558,8 pm ja hypotenuusan pituus on neljä Ca:n atomisädettä:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}\longrightarrow {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}}{16}}=\text{197.6 pmg Ca:n säteelle}.

Part 2

Tiheys saadaan kaavalla \text{density}=\dfrac{\text{mass}}{\text{volume}}. Kalsiumin tiheys saadaan selville määrittämällä sen yksikkösolun tiheys: esimerkiksi yksikkösolun sisältämä massa jaettuna yksikkösolun tilavuudella. Kasvokeskisessä Ca:n yksikkösolussa on kahdeksasosa atomista jokaisessa kahdeksassa kulmassa \left(8\times \dfrac{1}{8}=1\text{ atomi}\right) ja puolet atomista jokaisella kuudella pinnalla \left(6\times \dfrac{1}{2}=3\text{ atomeja}\right), eli yksikkösolussa on yhteensä neljä atomia.

Yksikkösolun massa saadaan:

\text{1 Ca:n yksikkösolu}\times \dfrac{\text{4 Ca-atomia}}{\text{1 Ca:n yksikkösolu}}\times \dfrac{\text{1 mol Ca}}{6.022\times {10}^{23}\text{Ca-atomit}}\times \dfrac{40.078\text{g}}{\text{1 mol Ca}}=2.662\times {10}^{-22}\text{g}

Ca-yksikkösolun tilavuus saadaan:

V={a}^{3}={(558.8\times {10}^{-10}\text{cm})}^{3}=1.745\times {10}^{-22}{\text{cm}}^{3}

(Huomaa, että reunan pituus muunnettiin pm:stä cm:ksi, jotta tiheydelle saatiin tavalliset tilavuusyksiköt.)

Tällöin tiheys \text{Ca}=\dfrac{2.662\times {10}^{-22}\text{g}}{1.745\times {10}^{-22}{\text{cm}}}^{3}}}={\text{1.53 g/cm}}^{3}

Tarkista oppimasi

Hopea kiteytyy FCC-rakenteeseen. Sen yksikkösolun reunan pituus on 409 pm.

1. Mikä on Ag:n atomisäde tässä rakenteessa?
2. Laske Ag:n tiheys.

Näytä ratkaisut

1. 144 pm
2. 10.5 g/cm3

Yleisesti yksikkösolu määritellään kolmen akselin (a, b ja c) pituuksien ja niiden välisten kulmien (α, β ja γ) avulla, kuten kuvassa 10 on esitetty. Akselit määritellään avaruusristikon pisteiden välisiksi pituuksiksi. Näin ollen yksikkösolun akselit yhdistävät pisteitä, joilla on identtiset ympäristöt.

Kuva 10. Yksikkösolu määritellään sen kolmen akselin (a, b ja c) pituuksien ja akselien välisten kulmien (α, β ja γ) avulla.

Seitsemän erilaista ristikkojärjestelmää, joista joissakin on useampi kuin yksi ristikkotyyppi, eli yhteensä neljätoista erilaista yksikkösolua, joilla on kuvassa 11 esitetyt muodot.

Kuva 11. Yksikkösolut. On olemassa seitsemän erilaista ristikkojärjestelmää ja 14 erilaista yksikkösolua.

Ionikiteiden rakenteet

Ionikiteet koostuvat kahdesta tai useammasta erityyppisestä ionista, jotka ovat yleensä erikokoisia. Näiden ionien pakkautuminen kiderakenteeseen on monimutkaisempaa kuin samankokoisten metalliatomien pakkautuminen.

Useimmat yksiatomiset ionit käyttäytyvät varattuina palloina, ja niiden vetovoima vastakkaisen varauksen omaavia ioneja kohtaan on sama joka suuntaan. Näin ollen ionisten yhdisteiden stabiilit rakenteet syntyvät, (1) kun yhden varauksen ioneja ympäröi mahdollisimman monta vastakkaisen varauksen ionia ja (2) kun kationit ja anionit ovat kosketuksissa toisiinsa. Rakenteet määräytyvät kahden päätekijän mukaan: ionien suhteelliset koot sekä positiivisten ja negatiivisten ionien lukumäärän suhde yhdisteessä.

Kuva 12. Kationit voivat miehittää anionien välissä kahdenlaisia reikiä: oktaedrisiä reikiä tai tetraedrisiä reikiä.

Yksinkertaisissa ionirakenteissa anionit, jotka ovat tavallisesti kationeja suurempia, on tavallisesti järjestetty lähimpänä toisiaan olevaan joukkoon. (Kuten aiemmin nähtiin, samaan ytimeen vetäytyvät lisäelektronit tekevät anioneista suurempia ja vähemmän samaan ytimeen vetäytyvät elektronit tekevät kationeista pienempiä verrattuna atomeihin, joista ne muodostuvat). Pienemmät kationit valtaavat yleensä jommankumman anionien väliin jäävistä kahdentyyppisistä rei’istä (tai väleistä). Pienempi rei’istä sijaitsee kolmen anionin välissä yhdessä tasossa ja yhden anionin välissä viereisessä tasossa. Tätä reikää ympäröivät neljä anionia on sijoitettu tetraedrin kulmiin, joten reikää kutsutaan tetraedrin reiäksi. Suurempi reikätyyppi löytyy kuuden anionin (kolme yhdessä tasossa ja kolme viereisessä tasossa) keskeltä, jotka sijaitsevat oktaedrin kulmissa; tätä kutsutaan oktaedriseksi reiäksi. Kuva 12 havainnollistaa näitä molempia reikätyyppejä.

Kationien ja anionien suhteellisesta koosta riippuen ionisen yhdisteen kationit voivat sijaita tetraedrisissä tai oktaedrisissä rei’issä, kuten kuvassa 13 on esitetty. Suhteellisen pienet kationit valtaavat tetraedrisiä reikiä ja suuremmat kationit oktaedrisiä reikiä. Jos kationit ovat liian suuria mahtuakseen oktaedrisiin reikiin, anionit voivat omaksua avoimemman rakenteen, kuten yksinkertaisen kuutiomuodon. Suuremmat kationit voivat tällöin miehittää suuremmat kuutioreiät, jotka avoimemmat välit mahdollistavat.

Kuva 13. Kationin koko ja yhdisteen valtaaman reiän muoto ovat suorassa yhteydessä toisiinsa.

Joko HCP- tai CCP-anionirivistössä on kaksi tetraedristä reikää kutakin anionia kohti. Yhdisteen, joka kiteytyy anionien tiiviimmin pakattuun anionirivistöön, jossa kationit ovat tetraedrin rei’issä, kationi:anioni-suhde voi olla maksimissaan 2:1; kaikki tetraedrin reiät täyttyvät tässä suhteessa. Esimerkkejä ovat Li2O, Na2O, Li2S ja Na2S. Yhdisteet, joiden suhde on pienempi kuin 2:1, voivat myös kiteytyä anionien ja kationien tiiviimmin pakkautuneena ryhmänä tetraedrin reikiin, jos ionikoot sopivat. Näissä yhdisteissä osa tetraedrin rei’istä jää kuitenkin tyhjiksi.

Octaedristen reikien ja anionien suhde joko HCP- tai CCP-rakenteessa on 1:1. Siten yhdisteiden, joissa kationit ovat oktaedrin rei’issä anionien lähimpään pakkaukseen sijoitetuissa rei’issä, kationi:anioni-suhde voi olla enintään 1:1. Esimerkiksi NiO:ssa, MnS:ssä, NaCl:ssä ja KH:ssa kaikki oktaedrin reiät ovat täynnä. Suhteita alle 1:1 havaitaan, kun osa oktaedrin rei’istä jää tyhjiksi.

Yksinkertaisessa kuutiomaisessa anionirivistössä on jokaista anionirivistön anionia kohti yksi kuutioreikä, jonka voi miehittää kationi. CsCl:ssä ja muissa rakenteeltaan samanlaisissa yhdisteissä kaikki kuutioreiät ovat varattuja. SrH2:ssa, UO2:ssa, SrCl2:ssa ja CaF2:ssa puolet kuutiorei’istä on varattu.

Erilaiset ioniyhdisteet kiteytyvät usein samaan rakenteeseen, kun niiden ionien suhteelliset koot ja stoikiometriat (kaksi tärkeintä ominaisuutta, jotka määräävät rakenteen) ovat samanlaisia.

Ioniyhdisteiden yksikkösolut

Monet ioniyhdisteet kiteytyvät kuutiomaisiin yksikkösoluihin, ja käytämme näitä yhdisteitä kuvaamaan ionirakenteiden yleisiä piirteitä.

Kun ioniyhdiste koostuu samankokoisista kationeista ja anioneista suhteessa 1:1, se muodostaa tyypillisesti yksinkertaisen kuutiorakenteen. Cesiumkloridi, CsCl, (kuvassa 14) on esimerkki tästä, sillä Cs+:n ja Cl-:n säteet ovat 174 pm ja 181 pm. Voimme ajatella tämän niin, että kloridi-ionit muodostavat yksinkertaisen kuutiomaisen yksikkösolun, jonka keskellä on cesiumioni; tai niin, että cesiumionit muodostavat yksikkösolun, jonka keskellä on kloridi-ioni; tai niin, että Cs+ -ionien muodostamat yksinkertaiset kuutiomaiset yksikkösolut ovat päällekkäin Cl-ionien muodostamien yksikkösolujen kanssa. Cesiumionit ja kloridi-ionit koskettavat yksikkösolujen rungon lävistäjiä pitkin. Yhdessä yksikkösolussa on yksi cesiumioni ja yksi kloridi-ioni, jolloin cesiumkloridin kaavan edellyttämä stoikiometria on l:l. Huomaa, että solun keskellä ei ole ristikkopistettä, eikä CsCl ole BCC-rakenne, koska cesiumioni ei ole identtinen kloridi-ionin kanssa.

Kuva 14. Ioniset yhdisteet, joissa on samankokoisia kationeja ja anioneja, kuten CsCl, muodostavat yleensä yksinkertaisen kuutiorakenteen. Niitä voidaan kuvata yksikkösoluilla, joiden kulmissa on joko kationit tai anionit.

Olemme sanoneet, että ristikkopisteiden sijainti on mielivaltainen. Tätä havainnollistaa CsCl-rakenteen vaihtoehtoinen kuvaus, jossa ristikkopisteet sijaitsevat cesiumionien keskuksissa. Tässä kuvauksessa cesiumionit sijaitsevat ristikkopisteissä solun kulmissa, ja kloridi-ioni sijaitsee solun keskellä. Nämä kaksi yksikkösolua ovat erilaisia, mutta ne kuvaavat identtisiä rakenteita.

Kun ioniyhdiste koostuu 1:1-suhteessa kationeista ja anioneista, jotka eroavat toisistaan merkittävästi kooltaan, se kiteytyy tyypillisesti FCC-yksikkösoluun, kuten kuvassa 15 on esitetty. Natriumkloridi, NaCl, on esimerkki tästä, sillä Na+:n ja Cl-:n säteet ovat 102 pm ja 181 pm. Voimme ajatella, että kloridi-ionit muodostavat FCC-solun, jossa natriumionit sijaitsevat solun reunojen keskellä ja solun keskellä olevissa oktaedrimaisissa rei’issä. Natrium- ja kloridi-ionit koskettavat toisiaan solun reunoilla. Yksikkösolussa on neljä natriumionia ja neljä kloridi-ionia, jolloin saadaan kaavan NaCl edellyttämä stoikiometria 1:1.

Kuva 15. Ioniset yhdisteet, joiden anionit ovat paljon suurempia kuin kationit, kuten NaCl, muodostavat yleensä FCC-rakenteen. Niitä voidaan kuvata FCC-yksikkösoluilla, joissa kationit ovat oktaedrimaisissa rei’issä.

Sinkkisulfidin kuutiomuoto, sinkkiblendi, kiteytyy myös FCC-yksikkösoluun, kuten kuvassa 16 on esitetty. Tämä rakenne sisältää sulfidi-ioneja FCC-ristikon hilapisteissä. (Sulfidi-ionien sijoittelu on sama kuin kloridi-ionien sijoittelu natriumkloridissa). Sinkki-ionin säde on vain noin 40 % sulfidi-ionin säteestä, joten nämä pienet Zn2+-ionit sijaitsevat vuorottelevissa tetraedrisissä rei’issä eli toisella puolella tetraedrisiä reikiä. Yksikkösolussa on neljä sinkki-ionia ja neljä sulfidi-ionia, jolloin saadaan empiirinen kaava ZnS.

Kuva 16. ZnS, sinkkisulfidi (tai sinkkiblende) muodostaa FCC-yksikkösolun, jossa sulfidi-ionit ovat ristikkopisteissä ja paljon pienemmät sinkki-ionit valtaavat puolet rakenteen tetraedrisistä rei’istä.

Kalsiumfluoridin yksikkösolu, kuten kuvassa 17 on esitetty, on niin ikään FCC-yksikkösolu, mutta tässä tapauksessa kationit sijaitsevat ristikkopisteissä; ekvivalenttiset kalsium-ionit sijoittuvat FCC-ristikon ristikoiden pisteisiin. Kalsiumionien FCC-ristikon kaikki tetraedriset paikat ovat fluoridi-ionien miehittämiä. Yksikkösolussa on neljä kalsiumionia ja kahdeksan fluoridi-ionia, joten kalsium:fluori-suhde on 1:2, kuten kemiallinen kaava CaF2 edellyttää. Kuvan 17 lähempi tarkastelu paljastaa yksinkertaisen kuutiomaisen fluoridi-ionien ruudukon, jossa kalsiumionit ovat puolessa kuution rei’istä. Rakennetta ei voida kuvata fluoridi-ionien pisteiden avaruusristikon avulla, koska kaikilla fluoridi-ioneilla ei ole samanlaisia ympäristöjä. Neljän kalsiumionin orientaatio fluoridi-ionien suhteen on erilainen.

Kuva 17. Kalsiumfluoridi, CaF2, muodostaa FCC-yksikkösolun, jossa kalsiumionit (vihreät) ovat ristikkopisteissä ja fluoridi-ionit (punaiset) miehittävät kaikki niiden väliset tetraedriset paikat.

Ionisäteiden laskeminen

Jos tiedämme ionisen yhdisteen yksikkösolun reunan pituuden ja ionien sijainnin solussa, voimme laskea ionisäteet yhdisteen ioneille, jos teemme oletuksia yksittäisten ionien muodoista ja kontakteista.

Esimerkki 5: Ionisäteiden laskeminen

LiCl:n (NaCl:n kaltainen rakenne, FCC) yksikkösolun reunan pituus on 0.514 nm eli 5,14 Å. Olettaen, että litiumioni on niin pieni, että kloridi-ionit ovat kosketuksissa, kuten kuvassa 15, laske kloridi-ionin ionisäde.

Huomautus: Pituusyksikköä angström, Å, käytetään usein kuvaamaan atomimittakaavan ulottuvuuksia, ja se vastaa 10-10 m.

Näytä ratkaisu

LiCl-yksikkösolun pinnalla kloridi-ionit ovat kosketuksissa toisiinsa pinnalla olevan diagonaalin poikki:

Piirretään suorakulmainen kolmio yksikkösolun pinnalle, ja nähdään, että lävistäjän pituus on yhtä suuri kuin neljä kloridin sädettä (yksi säde jokaisesta kulmakloridista ja yksi halkaisija – joka vastaa kahta sädettä – kloridi-ionista pinnan keskellä), joten d = 4r. Pythagoraan lauseesta saadaan:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}

josta saadaan:

\left(0.514\text{ nm}\right)^{2}+\left(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1.82 Å) Cl- säteelle

Check Your Learning

KCl:n (NaCl:n kaltainen rakenne, FCC) yksikkösolun reunan pituus on 6.28 Å. Olettaen anionin ja kationin kosketuksen solun reunaa pitkin, laske kaliumionin säde. Kloridi-ionin säde on 1,82 Å.

Näytä ratkaisu

Kalium-ionin säde on 1,33 Å.

On tärkeää ymmärtää, että yksikkösolujen reunapituuksien perusteella lasketut ionisäteiden arvot riippuvat lukuisista olettamuksista, kuten ionien täydellisestä pallonmuodosta, jotka ovat parhaimmillaankin likiarvoja. Näin ollen tällaiset lasketut arvot ovat itsessään likimääräisiä, eikä vertailuja voida viedä liian pitkälle. Menetelmä on kuitenkin osoittautunut käyttökelpoiseksi ionisäteiden laskemisessa kokeellisista mittauksista, kuten röntgenkristallografisista määrityksistä.

Röntgenkristallografia

Yksikkösolun koko ja atomien sijoittelu kiteessä voidaan määrittää mittauksista, jotka koskevat röntgensäteilyn diffraktiota kiteessä, jota kutsutaan röntgenkristallografiaksi. Diffraktio on sähkömagneettisen aallon kokema kulkusuunnan muutos, kun se kohtaa fysikaalisen esteen, jonka mitat ovat verrattavissa valon aallonpituuteen. Röntgensäteet ovat sähkömagneettista säteilyä, jonka aallonpituus on suunnilleen yhtä pitkä kuin naapuriatomien välinen etäisyys kiteissä (muutaman Å:n luokkaa).

Kun monokromaattinen röntgensäteilysäde osuu kiteeseen, sen säteet hajoavat kaikkiin suuntiin kiteen sisällä oleviin atomeihin. Kun samaan suuntaan kulkevat sirontaaallot kohtaavat toisensa, niissä tapahtuu interferenssi, prosessi, jossa aallot yhdistyvät niin, että amplitudi (intensiteetti) joko kasvaa tai pienenee riippuen siitä, missä määrin yhdistyvien aaltojen maksimit ovat erillään toisistaan (ks. kuva 18).

Kuva 18. Valoaallot, jotka ovat samassa tilassa, kokevat interferenssiä, jolloin ne yhdistyvät muodostaen suuremman (a) tai pienemmän (b) intensiteetin omaavia aaltoja riippuen niiden maksimien ja minimien välisestä etäisyydestä.

Kun röntgensäteet, joiden aallonpituus λ on tietty, sirontuvat atomeihin, jotka ovat vierekkäisissä kristallitasoissa, jotka on erotettu toisistaan etäisyyden d etäisyydellä toisistaan, ne voivat kokea konstruktiivista interferenssiä, kun näiden kahden aallon ennen yhdistymistä kulkemien etäisyyksien ero on aallonpituussuhteen kertoimella n. Aallonpituussuhteet voivat kuitenkin erota. Tämä ehto täyttyy, kun taittuneen säteen kulma θ suhteutetaan aallonpituuteen ja atomien väliseen etäisyyteen yhtälöllä:

n{\lambda }=2d\text{sin}\theta

Tämä suhde tunnetaan Braggin yhtälönä ilmiön ensimmäisenä selittäneen englantilaisen fyysikon W. H. Braggin kunniaksi. Kuvassa 19 on kaksi esimerkkiä diffraktoituneista aalloista kahdesta samasta kiteetasosta. Vasemmanpuoleinen kuva kuvaa Braggin kulmassa diffraktoituneita aaltoja, jolloin syntyy konstruktiivinen interferenssi, kun taas oikeanpuoleinen kuva kuvaa diffraktiota ja erilaista kulmaa, joka ei täytä Braggin ehtoa, jolloin syntyy destruktiivinen interferenssi.

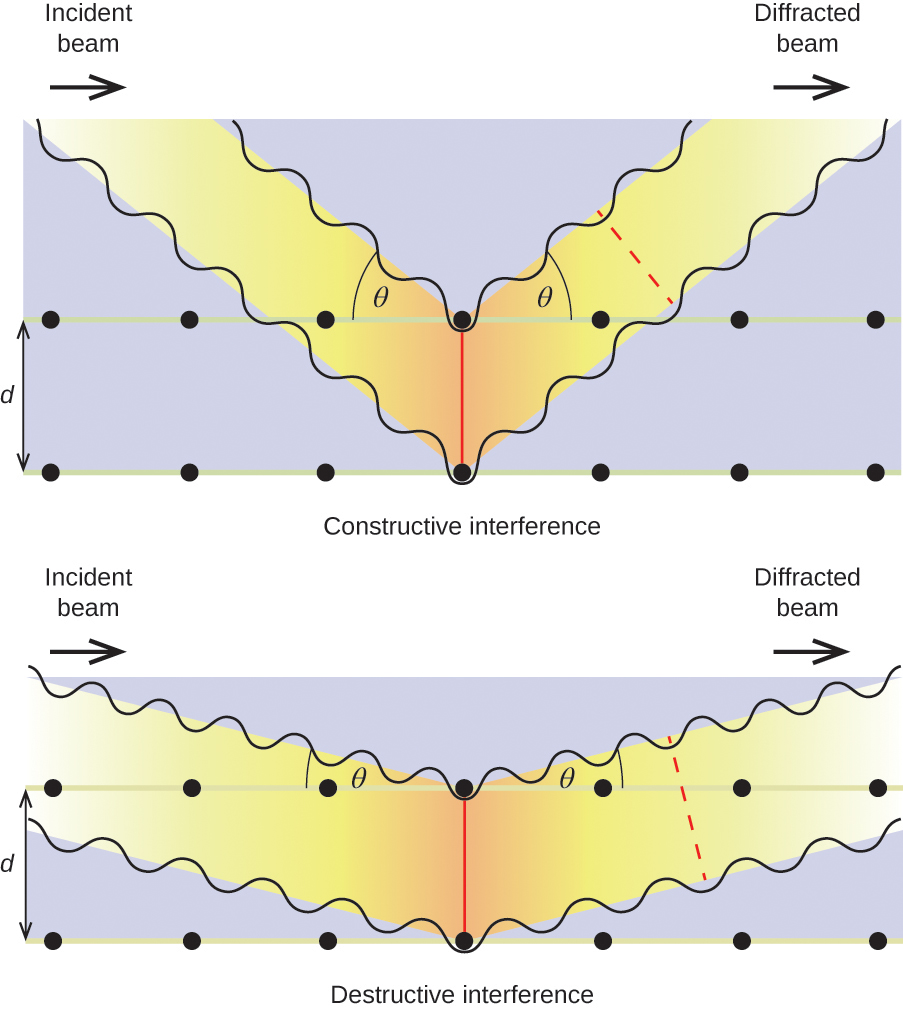
Kuva 19. Kiteen sisällä olevien atomien sirottamien röntgensäteiden diffraktio mahdollistaa atomien välisen etäisyyden määrittämisen. Ylimmässä kuvassa on kahden sironneen aallon välinen konstruktiivinen interferenssi ja tuloksena syntyvä diffraktoitunut aalto, jonka intensiteetti on suuri. Alimmassa kuvassa on destruktiivinen interferenssi ja matalan intensiteetin diffraktoitunut aalto.

Kuvassa 20 esitetyn kaltaista röntgendiffraktometriä voidaan käyttää mittaamaan kulmia, joissa röntgensäteet taittuvat vuorovaikutuksessa kiteen kanssa edellä kuvatulla tavalla. Tällaisista mittauksista voidaan käyttää Braggin yhtälöä atomien välisten etäisyyksien laskemiseen, kuten seuraavassa esimerkkiharjoituksessa osoitetaan.

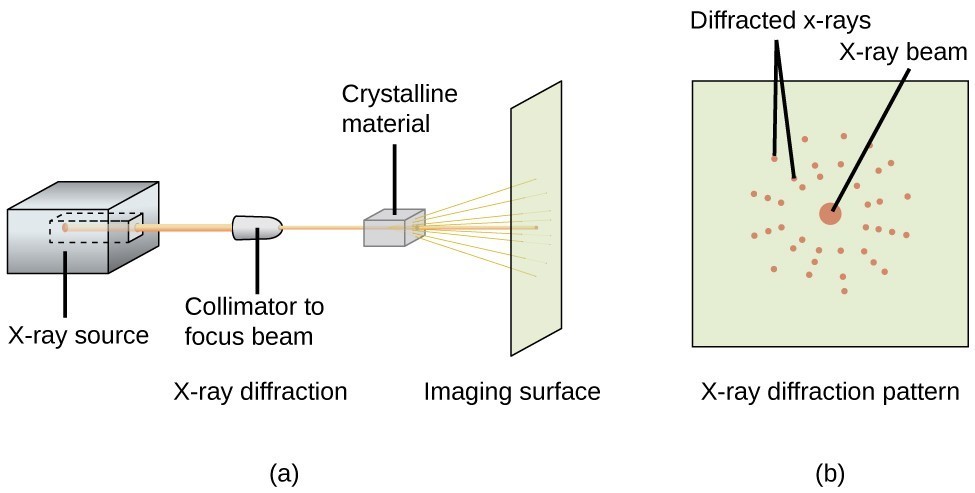
Kuva 20. Diffraktometrissä (a) röntgensäteen säde osuu kiteiseen materiaaliin, jolloin syntyy röntgendiffraktiokuvio (b), jota voidaan analysoida kiderakenteen määrittämiseksi.

Voit katsoa transkriptin ”Celebrating Crystallography – An animated adventure” täältä (avautuu uuteen ikkunaan).

Kemistin muotokuva: X-ray Crystallographer Rosalind Franklin

Kuva 21. Tässä kuvituksessa on röntgendiffraktiokuva, joka on samanlainen kuin Franklinin tutkimuksissaan löytämä kuva. (luotto: National Institutes of Health)

Francis Crickin ja James Watsonin vuonna 1953 tekemä DNA:n rakenteen löytäminen on yksi tieteen historian suurista saavutuksista. Heille myönnettiin vuonna 1962 Nobelin fysiologian tai lääketieteen palkinto yhdessä Maurice Wilkinsin kanssa, joka toimitti kokeellisen todisteen DNA:n rakenteesta. Brittiläinen kemisti Rosalind Franklin antoi korvaamattoman arvokkaan panoksen tähän monumentaaliseen saavutukseen mittaamalla röntgendiffraktiokuvia DNA:sta. Uransa alkuvaiheessa Franklinin tutkimus hiilen rakenteesta osoittautui hyödylliseksi Britannian sotatoimille. Siirryttyään 1950-luvun alussa biologisiin järjestelmiin Franklin ja tohtoriopiskelija Raymond Gosling havaitsivat, että DNA koostuu kahdesta muodosta: pitkästä, ohuesta kuidusta, joka muodostuu märkänä (B-tyyppi), ja lyhyestä, leveästä kuidusta, joka muodostuu kuivattuna (A-tyyppi). Hänen röntgendiffraktiokuvansa DNA:sta (kuva 21) antoivat ratkaisevan tärkeää tietoa, jonka avulla Watson ja Crick pystyivät vahvistamaan, että DNA muodostaa kaksoiskierteen, ja määrittelemään sen koon ja rakenteen yksityiskohdat.

Franklin teki myös uraauurtavaa tutkimusta viruksista ja niiden geneettistä informaatiota sisältävästä RNA:sta ja löysi uutta tietoa, joka muutti radikaalisti alan tietämystä. Sairastuttuaan munasarjasyöpään Franklin jatkoi työtään kuolemaansa saakka vuonna 1958 37-vuotiaana. Monista hänen työnsä postuumisti annetuista tunnustuksista mainittakoon, että Finch University of Health Sciences -yliopiston Chicagon lääketieteellinen tiedekunta muutti nimensä Rosalind Franklin University of Medicine and Science -yliopistoksi vuonna 2004 ja otti viralliseksi yliopistotunnuksekseen kuvan hänen kuuluisasta röntgendiffraktiokuvastaan DNA:sta.

Sanasto

kappalekeskeinen kuutiomainen (BCC) kiinteä aine: kiderakenne, jolla on kuutiomainen yksikkösolu, jonka kulmissa ja keskellä on ristikkopisteet

kappalekeskeinen kuutiomainen yksikkösolu: Kappalekeskeisen kuutiokiteen yksinkertaisin toistuva yksikkö; se on kuutio, jossa on ristikkopisteitä kussakin kulmassa ja kuution keskellä

Braggin yhtälö: yhtälö, joka suhteuttaa kulmat, joilla röntgensäteet taittuvat kiteen sisällä oleviin atomeihin

koordinaatioluku: kiteessä olevaa tiettyä atomia tai kompleksissa olevaa keskimmäistä metalliatomia lähimpänä olevien atomien lukumäärä

kuutiopakkaus (CCP): Kiderakenne, jossa tiiviisti pakattujen atomien tai ionien tasot ovat pinoutuneet kolmen vuorottelevan kerroksen sarjana, joilla on erilainen suhteellinen suuntaus (ABC)

diffraktio: Sähkömagneettisen säteilyn uudelleen suuntautuminen, joka tapahtuu, kun se kohtaa sopivan kokoisen fysikaalisen esteen

pintakeskitetty kuutiomainen (FCC) kiinteä aine: Kiderakenne, joka koostuu kuutiollisesta yksikkösolusta, jossa on ristikkopisteitä kunkin pinnan kulmissa ja keskellä

pintakeskitetty kuutiollinen yksikkösolu: yksinkertaisin toistuva yksikkö kasvokeskisessä kuutiokiteessä; se on kuutio, jossa on ristikkopisteitä jokaisessa kulmassa ja jokaisen sivun keskellä

heksagonaalinen lähipakkaus (HCP): kiderakenne, jossa tiiviisti pakkautuneet atomi- tai ionikerrokset ovat pinoutuneet sarjana kahta vuorottelevaa kerrosta, joilla on erilainen suhteellinen orientaatio (AB)

reikä: (myös väli) atomien välinen tila kiteessä

isomorfinen: jolla on sama kiderakenne

oktaedrinen reikä: avoin tila kiteessä oktaedrin kulmissa sijaitsevien kuuden hiukkasen keskellä

yksinkertainen kuutiollinen yksikkösolu: (myös primitiivinen kuutiollinen yksikkösolu) yksinkertaisen kuutiorakenteen yksikkösolu

yksinkertainen kuutiorakenne: kiderakenne, jossa on kuutiomainen yksikkösolu, jonka ristikkopisteet ovat vain kulmissa

avaruusristikko: kaikki kiteen sisällä olevat pisteet, joilla on identtiset ympäristöt

tetraedrinen reikä: neljän atomin tai ionin muodostama tetraedrinen tila kiteessä

yksikkösolu: avaruusristikon pienin osa, joka toistuu kolmiulotteisesti muodostaen koko ristikon

röntgenkristallografia: kokeellinen tekniikka, jolla määritetään atomien väliset etäisyydet kiteessä mittaamalla kulmia, joilla röntgensäteet taittuvat kulkiessaan kiteen läpi

.