Mitä hyötyä merkkitaulukoista on?
Tässä vaiheessa on hyvä kysyä: mitä järkeä on opetella merkkitaulukoita? Yksinkertainen vastaus on, että molekyylin symmetriaa ja siihen liittyvää merkkitaulukkoa voidaan käyttää monien kemiallisesti merkittävien spektroskopioiden sekä sidosten tulkitsemiseen ja ennustamiseen. Havainnollistamme tätä seuraavaksi keskittymällä molekyylin värähtelymoodeihin.
Laboratoriossa voimme kerätä hyödyllistä kokeellista tietoa infrapuna- (IR) ja Raman-spektroskopian avulla. Näitä tietoja voidaan verrata IR- ja/tai Raman-aktiivisten kaistojen lukumäärään, joka ennustetaan ryhmäteorian ja oikean merkkitaulukon soveltamisesta. Tämän käsittelyn taustalla oleva matematiikka (ryhmäteoria ja matriisialgebra) toimii vankkana teoreettisena perustana. Jäljempänä kuvatut käsittelyt toimivat, koska kaikki molekyylin symmetriaoperaatiot muodostavat matemaattisen ryhmän ja noudattavat ryhmän sääntöjä. Kuten aiemmin todettiin, meidän ei tarvitse hallita tätä matematiikan osa-aluetta voidaksemme hyödyntää merkkitaulukoita hyvin.
Vapausasteet ja värähtelyt molekyyleissä
Tässä käsitellään aluksi yksinkertaisen molekyylin (vesi) vapausasteita. Näemme hyvin nopeasti, miksi on erittäin hyödyllistä käyttää symmetriaa, kun tutkitaan suurempia molekyylejä.
Molekyylissä, jossa on ”N” atomia, on 3N vapausastetta (muistakaa, että elämme kolmiulotteisessa maailmassa, jossa on x-, y- ja z-koordinaatit). Epälineaariselle molekyylille 3 vapausastetta voidaan merkitä translaatioille – koko kappaleen liikkeelle (Tx, Ty, Tz) ja 3 rotaatioille (Rx, Ry, Rz). Muut atomien liikkeet ovat atomien siirtymiä keskiasemistaan – painopiste ei muutu. Näitä perusvärähtelyjä kutsutaan ”normaalimoodeiksi”. Epälineaarisella molekyylillä on siis 3N-6 normaalimoodia. Vedellä normaalimoodien lukumäärä on 3 (3 x 3 – 6 = 3). Lineaarisilla molekyyleillä on 3N-5 normaalimoodia.
Vedelle, jota on tietenkin tutkittu intensiivisesti, tiedämme, että nämä 3 värähtelyä ovat seuraavat.
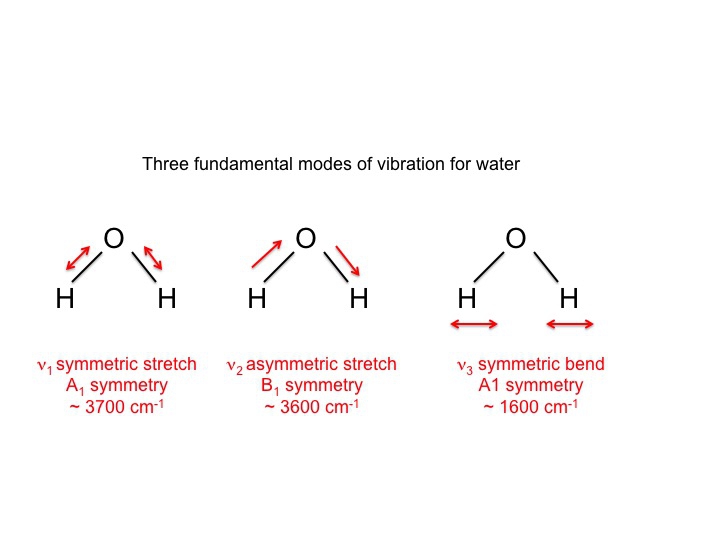
Symbolit, joita käytetään kuvaamaan näitä moodeja (A1, B1), ovat samoja Mulliken-symboleita, joihin törmäsimme keskustellessamme merkkitaulukoista. Toisin sanoen värähtelyjä, jotka ovat molekyylien ominaisuuksia, voidaan kuvata symmetrialajeilla tai redusoimattomilla esityksillä. Itse asiassa suuri osa värähtelyspektroskopiaan liittyvästä kirjallisuudesta käyttää näitä symboleja lyhennettynä tapana välittää tietoa.
Pitäisi olla melko ilmeistä, että värähtelyjen määrä kasvaa nopeasti molekyylin atomien lukumäärän kasvaessa jopa vaatimattomasti. Värähtelylajien määrittäminen tarkastelemalla (kuten teimme veden kohdalla) muuttuu nyt paljon vaikeammaksi. Tarkastellaan esimerkiksi seuraavia yhdisteitä:
H2O 3 atomia 3 värähtelyä
PH3 4 atomia 6 värähtelyä
CO22- 4 atomia 6 värähtelyä
XeF4 5 atomia 9 värähtelyä
B2H6 8 atomia 18 värähtelyä
Diboraanin (B2H6), jonka symmetria on D2h, kaikkien 18 värähtelyn luonteen ja symmetrialajin selvittäminen tarkastelemalla olisi pelottava tehtävä. Kuitenkin D2h:n merkkitaulukon ja symmetriaominaisuuksien tuntemuksen avulla kaikkien värähtelyjen symmetrialajien määrittäminen on suoraviivaista.
Veden tapauksessa voisimme esittää merkkitaulukon (C2v), jossa molekyylien ominaisuuksien sarakkeessa on lueteltuna 3 värähtelyä (ν1, v2, v3) alla esitetyllä tavalla. (ν = kreikkalainen symboli ”nu”)

Yleisesti tämä lähestymistapa on kuitenkin epäkäytännöllinen. Otetaan esimerkiksi pyridiini (C5H5N). Pisteryhmä on myös C2v, mutta molekyylissä on 11 atomia. Perusvärähtelymuotojen lukumäärä on 27 ( 3 x 11 – 6 = 27).
Tällöin meidän pitäisi laatia C2v-merkkitaulukko, josta näkyisivät kaikkien 27 värähtelyn symmetriat. Tästä syystä värähtelyjä ei yleensä sisällytetä merkkitaulukoihin. Sen sijaan käyttäjän (sinun) tehtävänä on määrittää värähtelyjen lukumäärä ja tyyppi (niiden symmetrialajien määrittelemänä) kaikille kohdattaville molekyyleille. Jäljempänä kuvataan, miten tämä tehdään.
Redusoituvat esitykset
Kuten aiemmin todettiin, yksi merkkitaulukoiden tärkeistä ominaisuuksista on se, että symmetriaoperaatiot ovat matemaattisen ryhmän jäseniä ja niiden välillä on tärkeitä suhteita. Yleisesti ottaen samaa voidaan sanoa molekyyliominaisuuksien symmetrialajeista eli redusoitumattomista esityksistä. Myös redusoitumattomien esitysten merkkien yhdistämisestä joko kertomalla tai yhteen-/subtraktiolla saadut tuotteet noudattavat ryhmän sääntöjä. Uudet esitykset eivät ole enää yksinkertaisimpia mahdollisia, vaan niitä kutsutaan ”redusoitaviksi esityksiksi”, koska ne voidaan ”pelkistää” osiinsa.
Veden kohdalla esimerkiksi translaatioiden (Tx, Ty, Tz) symmetriat (Tx, Ty, Tz) voidaan poimia suoraan C2v-merkkitaulukosta. Ne ovat A1, B1 ja B2. Voimme esittää kaikki nämä kolme vapausastetta esityksellä ΓT ja voimme kirjoittaa alla olevan lausekkeen. (Γ = kreikkalainen iso kirjain ”gamma”).
ΓT = A1 + B1 + B2
Tiedämme, että A1, B1 ja B2 ovat vain symmetrialajien (redusoimattomien esitysten) lyhennettyjä merkintöjä. Voimme siis yksinkertaisesti kirjoittaa ΓT:n merkit ylös laskemalla yhteen yksittäiset merkit A1:lle, B1:lle ja B2:lle C2v:n merkkitaulukosta.
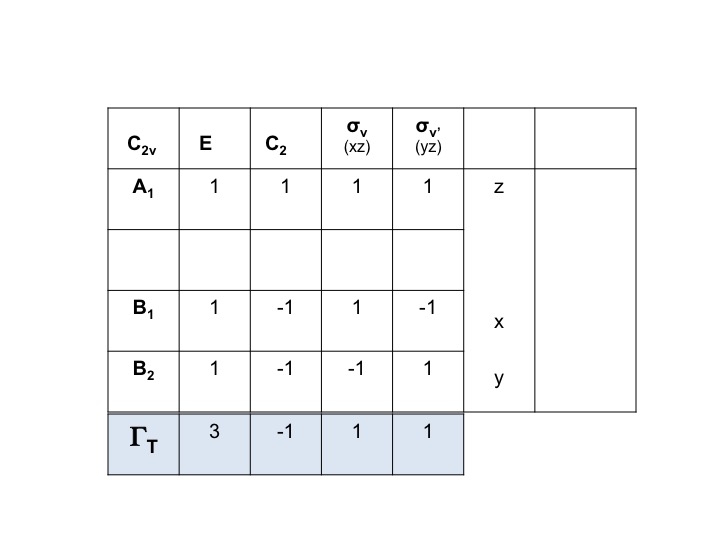
Siten ΓT = 3 -1 1 1.
Tämä on kelvollinen redusoituva esitys ja C2v-ryhmän jäsen.
Voidaan samalla tavalla kirjoittaa redusoituva esitys kaikille kolmelle rotaatiolle ja kaikille värähtelyille.
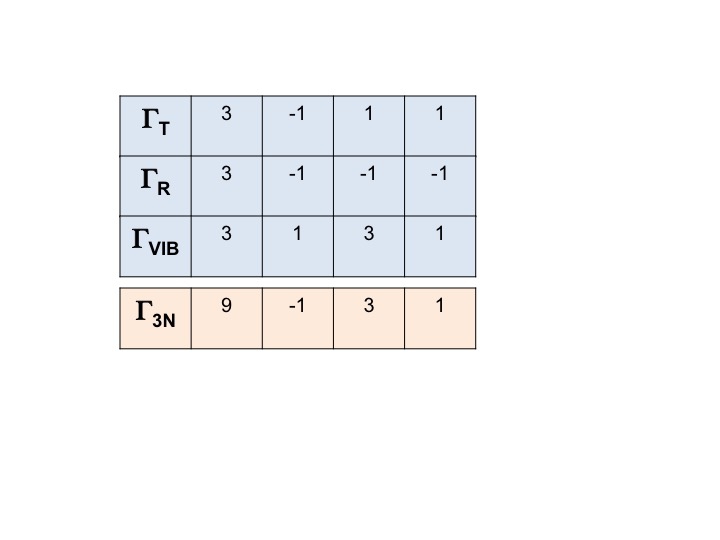
Molekyylin (3N) KAIKKIEN vapausasteiden esitys voidaan kirjoittaa muotoon
Γ3N = ΓT + ΓR + ΓVIB
ja sen redusoituva esitys saadaan yksinkertaisesti laskemalla yhteen ΓT:n, ΓR:n ja ΓVIB:n merkit.
Γ3N = 9 -1 3 1
Pane tämä muistiin – se tulee esiin myöhemmin!
Vaikka merkkijoukko 9 -1 3 1 on kelvollinen C2v-ryhmän jäsen, se ei ole erityisen käyttökelpoinen molekyylien ominaisuuksista keskusteltaessa. Se, mitä todella tarvitaan, on symmetrialajien pikakieli (Mullikenin symbolit, A1, B1 jne.). Toisin sanoen haluamme ilmaista Γ3N:n A1:n, B1:n jne. muodossa. Edellä käsitellyistä tiedoista voidaan helposti osoittaa tarkastelemalla, että:
Γ3N = 3A1 +A2 + 3B1 +2B2
Hyvä uutinen on, että muiden monimutkaisempien molekyylien kohdalla meidän ei tarvitse suorittaa tätä tehtävää tarkastelemalla, koska:
1. Voimme helposti generoida Γ3N redusoituvan esityksen molekyylille (jos tiedämme sen pisteryhmäsymmetrian).
2. Voimme helposti muuntaa Γ3N redusoituvan esityksen sen symmetrialajien (Mulliken-symbolien) summaksi käyttämällä ”yksinkertaista” kaavaa, jota kutsutaan reduktiokaavaksi.
Yleinen menetelmä Γ3N:n saamiseksi
Vaihe 1
Vastaanotetaan molekyylin merkkitaulukko ja lisätään rivi alareunaan. Luo tälle riville redusoituva esitys ΓT:lle (tai Γxyz:lle), kuten teimme edellä, yksinkertaisesti lisäämällä kullekin operaatiolle merkit, jotka vastaavat molekyylin ominaisuuksia x:lle, y:lle ja z:lle. C2v:n osalta olemme jo osoittaneet, että nämä ovat merkit, jotka vastaavat A1:tä, B1:tä ja B2:ta.
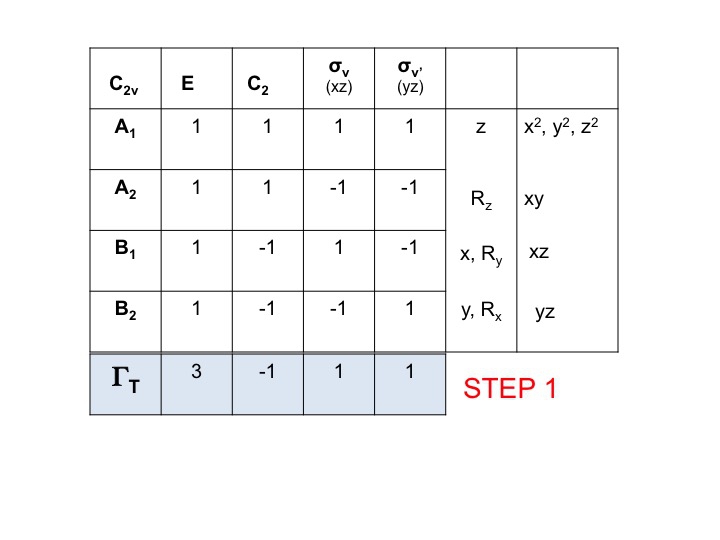
Vaihe 2
Lisää toinen rivi ΓT:n alapuolelle ja kirjoita ylös niiden atomien lukumäärä, jotka EIVÄT MUUTTAA sijaintiaan kunkin symmetriaoperaation aikana. Tässä vaiheessa huomaat, kuinka hyödyllinen todellinen molekyylimallisarja on. Tätä varten sinun on myös tiedettävä, missä symmetriaelementit ovat ja miten symmetriaoperaatiot vaikuttavat molekyyliin. Tietenkin osaat jo tehdä tämän, koska olet opiskellut Schönfliesin merkintätapaa ja tiedät, miten molekyylin pisteryhmä määritetään. Merkintätaulukossa on myös kaikki symmetriaoperaatiot lueteltu luokittain ylärivillä.
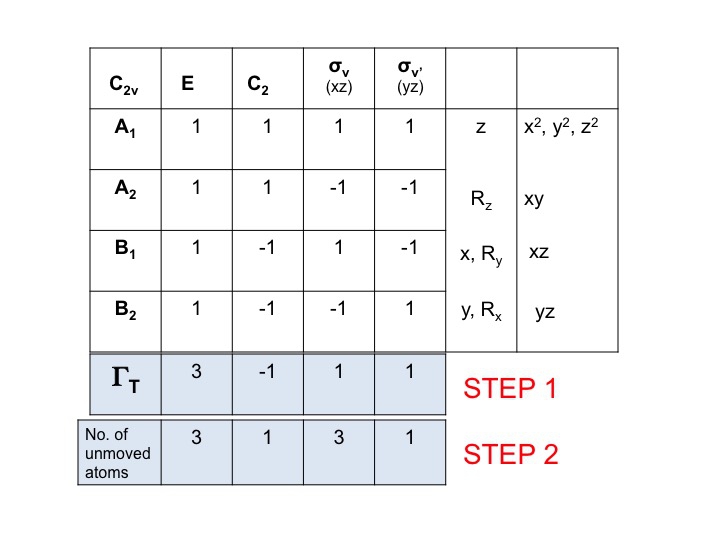
Veden (3 atomia) kohdalla E:n alla on siis 3 liikkumatonta atomia, mutta C2:n kohdalla molemmat H:t liikkuvat, mutta koska O-atomi istuu C2-akselilla, se ei muuta sijaintiaan, joten merkitään C2:n sarakkeen alle 1. Vaiheessa 2 luotu uusi lukujoukko (3 1 3 1) on myös redusoituva esitys C2v:ssä ja noudattaa ryhmän sääntöjä.
Vaihe 3
Vaiheessa 3
Tässä vaiheessa yksinkertaisesti kerromme yhteen vaiheissa 1 ja 2 luodut merkit. Tulos (kolmas rivi) on Γ3N:n (tai ΓTOT:n) redusoituva esitys. Se on niin yksinkertaista.
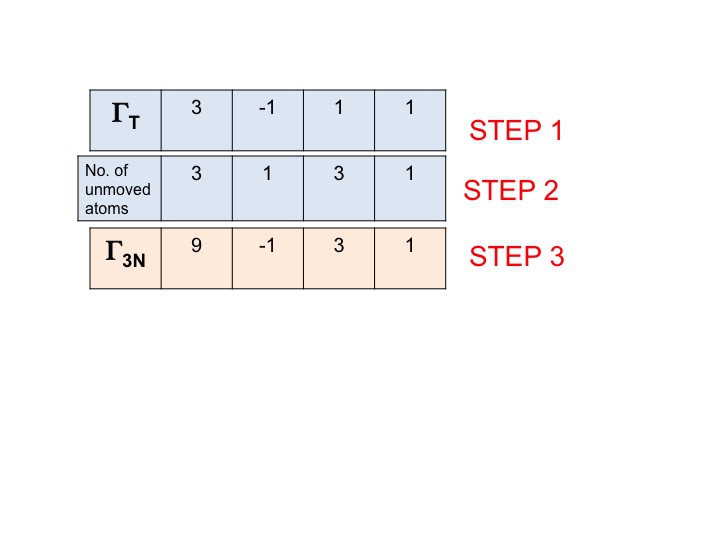
Huomaa, että uusi redusoituva esitys (9 -1 1 3) on identtinen Γ3N:n esityksen kanssa, jonka saimme aiemmin tarkastelemalla.
Redusoituvan esityksen redusoiminen
Muuttaaksemme MIKÄ tahansa redusoituvan esityksen sen redusoimattomien esitysten (symmetrialajien tai Mulliken-symbolien) summaksi käytämme redusointikaavaa:

Tämän tiedon löydät helposti merkkitaulukosta:
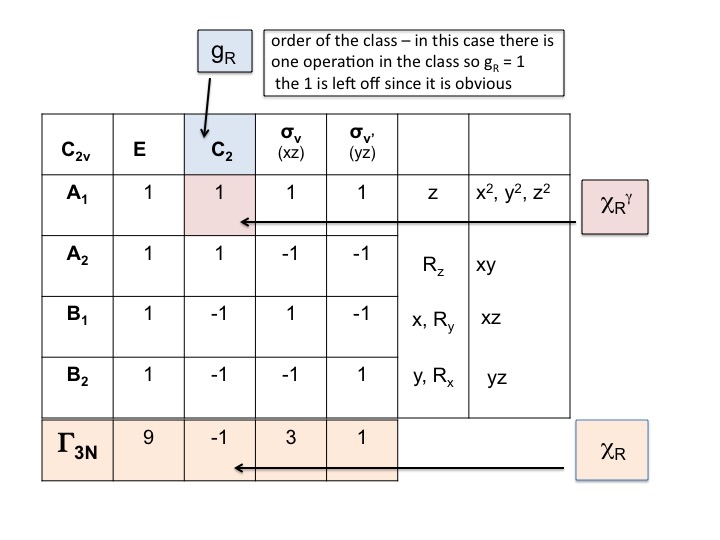
Palatakseni takaisin esimerkkiin veden osalta: Pisteryhmä C2v, järjestys (g) = 4
Redusoituva esitys Γ3N = 9 -1 3 1
Kertojen lukumäärä, jolloin A1 esiintyy tässä esityksessä, on siis
aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3
siten Γ3N sisältää 3 A1-symmetrialajia. Muiden symmetrialajien lukumäärät lasketaan seuraavasti:
aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 yksi A2 läsnä
aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 B1 present
aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1.1} = 2 2 B2 läsnä
Voidaan nyt kirjoittaa Γ3N = 3A1 + A2 + 3B1 + 2B2 (juuri se, minkä saimme edellä ”tarkastelemalla”. Voimme nyt vähentää translaatioiden ja rotaatioiden symmetrialajit, jolloin saamme värähtelyn perustilojen lukumäärän ja symmetrialajit. ΓT ja ΓR saadaan suoraan merkkitaulukosta.
Γ3N = 3A1 + A2 + 3B1 + 2B2
ΓT = A1 + B1 + B2
ΓR = A2 + B1 + B2
ΓVIB = Γ3N- – ΓT – ΓR = 2A1 +B1
Veden kolmella normaalivärähtelymoodilla on siis symmetriat A1, A1 ja B1.
Meillä on nyt käytössämme yleinen menetelmä molekyylin kaikkien perusvärähtelymoodien määrittämiseksi ja näiden moodien ilmaisemiseksi Mulliken-symbolien pikakielellä. Tämä on yksi harjoitustehtävistä, jotka testataan tentissä 1. Paras tapa saada varmuutta tähän menetelmään on harjoitella mahdollisimman monia mahdollisia esimerkkejä!
Seuraava: Valintasäännöt