Ein pythagoreisches Tripel ist ein Tripel aus den positiven ganzen Zahlen , und , so dass ein rechtwinkliges Dreieck mit den Schenkeln und der Hypotenuse existiert. Nach dem Satz des Pythagoras ist dies äquivalent dazu, positive ganze Zahlen , und zu finden, die

Das kleinste und bekannteste pythagoreische Tripel ist . Das rechtwinklige Dreieck mit diesen Seitenlängen wird manchmal als 3,4,5-Dreieck bezeichnet.

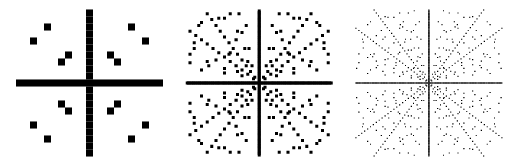
Darstellungen von Punkten in der -Ebene, für die ein pythagoräisches Tripel ist, sind oben für sukzessive größere Schranken dargestellt. Diese Diagramme schließen negative Werte von und ein und sind daher symmetrisch um die x- und y-Achse.

In ähnlicher Weise sind Diagramme von Punkten in der -Ebene, so dass ein pythagoräisches Tripel ist, oben für sukzessive größere Schranken dargestellt.

Es ist üblich, nur primitive pythagoräische Tripel (auch „reduzierte“ Tripel genannt) zu betrachten, in denen und relativ prim sind, da andere Lösungen trivial aus den primitiven erzeugt werden können. Die primitiven Dreiergruppen sind oben abgebildet, und es ist sofort zu erkennen, dass die radialen Linien, die in der ursprünglichen Darstellung den imprimitiven Dreiergruppen entsprechen, in dieser Abbildung fehlen. Bei primitiven Lösungen muss eine von oder gerade und die andere ungerade sein (Shanks 1993, S. 141), wobei immer ungerade ist.

Außerdem ist eine Seite jedes pythagoreischen Tripels durch 3, eine andere durch 4 und eine andere durch 5 teilbar. Eine Seite kann zwei dieser Teiler haben, wie in (8, 15, 17), (7, 24, 25) und (20, 21, 29), oder sogar alle drei, wie in (11, 60, 61).

Gegeben ein primitives Tripel , erhält man drei neue primitive Tripel aus

			(2)
			(3)
			(4)

wo

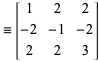		(5)
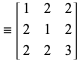		(6)
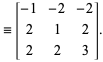		(7)

Hall (1970) und Roberts (1977) beweisen, dass ein primitives pythagoreisches Tripel ist, wennf

wobei ein endliches Produkt der Matrizen , , ist. Daraus folgt, dass jedes primitive pythagoräische Tripel ein Mitglied der unendlichen Matrix

Pythagoras und die Babylonier gaben eine Formel für die Erzeugung von (nicht notwendigerweise primitiven) Tripeln als

für , was eine Menge von eindeutigen Tripeln erzeugt, die weder alle primitiven noch alle imprimitiven Tripel enthält (und wo im Sonderfall , ).

Die frühen Griechen gaben

wobei und relativ prim und von entgegengesetzter Parität sind (Shanks 1993, p. 141), was eine Menge eindeutiger Tripel erzeugt, die genau die primitiven Tripel enthält (nach geeigneter Sortierung von und ).

Lass eine Fibonacci-Zahl sein. Dann

generiert eindeutige pythagoreische Tripel (Dujella 1995), wenn auch nicht erschöpfend für primitive oder imprimitive Tripel. Allgemeiner gesagt, ausgehend von den positiven ganzen Zahlen , und der Konstruktion der Fibonacci-ähnlichen Folge mit den Termen , , , , , … erzeugt verschiedene pythagoreische Tripel

(Horadam 1961), wobei

(Beiler 1966, p. 116). Man beachte, dass ist, wenn eine Primzahl oder eine doppelte Primzahl ist. Die ersten Zahlen für , 2, … sind 0, 0, 1, 1, 1, 1, 1, 2, 2, 1, 1, 4, 1, … (OEIS A046079).

Um die Anzahl der Möglichkeiten zu finden, auf die eine Zahl die Hypotenuse eines primitiven rechtwinkligen Dreiecks sein kann, schreibe ihre Faktorisierung als

wobei die s von der Form und die s von der Form sind. Die Anzahl der möglichen primitiven rechtwinkligen Dreiecke ist dann

Zum Beispiel, da

			(27)
			(28)

Die Werte von für , 2, … sind 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, … (OEIS A024362). Die ersten paar Primzahlen der Form sind 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, … (OEIS A002144), also sind die kleinsten Seitenlängen, die die Hypotenusen von 1, 2, 4, 8, 16, … primitiven rechtwinkligen Dreiecken sind 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).

Die Anzahl der möglichen primitiven oder nichtprimitiven rechtwinkligen Dreiecke mit als Hypotenuse ist

			(29)
			(30)

(korrigiert den Tippfehler von Beiler 1966, p. 117, der besagt, dass diese Formel nur die Anzahl der nicht-primitiven Lösungen angibt), wobei die Funktion der Summe der Quadrate ist. Zum Beispiel gibt es vier verschiedene ganzzahlige Dreiecke mit Hypotenuse 65, da

Die ersten Zahlen für , 2, … sind 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, … (OEIS A046080). Die kleinsten Hypotenusen mit verschiedenen Tripeln sind 1, 5, 25, 125, 65, 3125, … (OEIS A006339). Die folgende Tabelle enthält die Hypotenusen, für die es genau verschiedene rechtwinklige Dreiecke für , 1, …, 5 gibt.

	OEIS	Hypotenusen, für die es verschiedene ganzzahlige Dreiecke gibt
0	A004144	1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, …
1	A084645	5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, …
2	A084646	25, 50, 75, 100, 150, 169, 175, 200, 225, …
3	A084647	125, 250, 375, 500, 750, 875, 1000, 1125, 1375, …
4	A084648	65, 85, 130, 145, 170, 185, 195, 205, 221, 255, …
5	A084649	3125, 6250, 9375, 12500, 18750, 21875, 25000, …

Daher ist die Gesamtzahl der Möglichkeiten, auf die entweder ein Schenkel oder eine Hypotenuse eines rechtwinkligen Dreiecks sein kann, gegeben durch

Die Werte für , 2, … sind 0, 0, 1, 1, 2, 1, 1, 2, 2, 2, 1, 4, 2, 1, 5, 3, … (OEIS A046081). Die kleinsten Zahlen , die die Seiten von allgemeinen rechtwinkligen Dreiecken für , 2, … sein können, sind 3, 5, 16, 12, 15, 125, 24, 40, … (OEIS A006593; Beiler 1966, S. 114).

Es gibt 50 pythagoreische Tripel mit einer Hypotenuse kleiner als 100, von denen die ersten, sortiert nach aufsteigender , (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084, und A009000).

Von diesen sind nur 16 primitive Tripel mit einer Hypotenuse kleiner als 100: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89), und (65, 72, 97) (OEIS A046086, A046087, und A020882).

Lassen Sie die Anzahl der Tripel mit Hypotenuse als , die Anzahl der Tripel mit Hypotenuse als und die Anzahl der primitiven Tripel kleiner als als bezeichnen. Die folgende Tabelle fasst dann die Werte für Potenzen von 10 zusammen.

	OEIS	, , …
	A101929	1, 50, 878, 12467, …
	A101930	2, 52, 881, 12471, …
	A101931	1, 16, 158, 1593, …

Lehmer (1900) bewies, dass die Anzahl der primitiven Lösungen mit Hypotenuse kleiner als erfüllt

(OEIS A086201).

Die Inradien der ersten paar primitiven pythagoreischen Dreiecke, geordnet nach aufsteigenden , sind gegeben durch 1, 2, 3, 3, 3, 6, 5, 4, 10, 5, … (OEIS A014498).

Es gibt eine allgemeine Methode, um Dreiergruppen von pythagoräischen Dreiecken mit gleichen Flächen zu erhalten. Man nehme die drei Sätze der Generatoren als

			(34)
			(35)
			(36)
			(37)
			(38)
			(39)

Dann wird das rechte Dreieck, das durch jedes Tripel () einen gemeinsamen Flächeninhalt

(Beiler 1966, pp. 126-127). Das einzige Extremum dieser Funktion tritt bei auf. Da für , ist die kleinste Fläche, die sich drei nicht-primitive rechtwinklige Dreiecke teilen, gegeben durch , was eine Fläche von 840 ergibt und den Tripletts (24, 70, 74), (40, 42, 58) und (15, 112, 113) entspricht (Beiler 1966, S. 126).

Zu den rechtwinkligen Dreiecken, deren Flächeninhalt aus einer einzigen Ziffer besteht, gehören (Flächeninhalt von 6) und (Flächeninhalt von 666666; Wells 1986, S. 89).

Im Jahr 1643 forderte Fermat Mersenne auf, ein pythagoreisches Triplett zu finden, dessen Hypotenuse und Summe der Schenkel Quadrate sind. Fermat fand die kleinste derartige Lösung:

			(41)
			(42)
			(43)

mit

			(44)
			(45)

Ein verwandtes Problem ist es, zu bestimmen, ob eine bestimmte ganze Zahl der Flächeninhalt eines rechtwinkligen Dreiecks mit rationalen Seiten sein kann. 1, 2, 3 und 4 sind keine Flächen von rechtwinkligen Dreiecken mit rationalen Seiten, aber 5 ist (3/2, 20/3, 41/6), ebenso wie 6 (3, 4, 5). Die Lösung des Problems beinhaltet die elliptische Kurve

Eine Lösung (, , ) existiert, wenn (46) eine rationale Lösung hat, in diesem Fall

			(47)
			(48)

(Koblitz 1993). Es ist keine allgemeine Methode bekannt, um festzustellen, ob es eine Lösung für beliebige gibt, aber eine von J. Tunnell 1983 entwickelte Technik erlaubt es, bestimmte Werte auszuschließen (Cipra 1996).