Im siebzehnten und besonders im achtzehnten Jahrhundert, Jahrhunderts, getrieben von dem Wunsch, die Natur zu verstehen, und dem Bestreben, Ballons zu bauen, in denen sie fliegen konnten (Abbildung 1), stellten einige Wissenschaftler die Beziehungen zwischen den makroskopischen physikalischen Eigenschaften von Gasen her, d. h. Druck, Volumen, Temperatur und Menge des Gases. Obwohl ihre Messungen nach heutigen Maßstäben nicht präzise waren, konnten sie die mathematischen Beziehungen zwischen Paaren dieser Variablen (z. B. Druck und Temperatur, Druck und Volumen) bestimmen, die für ein ideales Gas gelten – ein hypothetisches Konstrukt, dem reale Gase unter bestimmten Bedingungen nahe kommen. Schließlich wurden diese einzelnen Gesetze in einer einzigen Gleichung zusammengefasst – dem idealen Gasgesetz -, das die Gasmengen für Gase in Beziehung setzt und für niedrige Drücke und moderate Temperaturen recht genau ist. Wir werden die wichtigsten Entwicklungen der einzelnen Beziehungen betrachten (aus pädagogischen Gründen nicht ganz in historischer Reihenfolge) und sie dann im idealen Gasgesetz zusammenfassen.

Abbildung 1. Im Jahr 1783 fand die erste (a) wasserstoffgefüllte Ballonfahrt, (b) bemannte Heißluftballonfahrt und (c) bemannte wasserstoffgefüllte Ballonfahrt statt. Als der in (a) dargestellte wasserstoffgefüllte Ballon landete, soll er von den verängstigten Dorfbewohnern von Gonesse mit Heugabeln und Messern zerstört worden sein. Der Start des letzteren wurde Berichten zufolge von 400.000 Menschen in Paris verfolgt.

Druck und Temperatur: Das Gay-Lussac’sche Gesetz

Stellen Sie sich vor, Sie füllen einen starren Behälter, der an einem Manometer befestigt ist, mit Gas und verschließen ihn dann, so dass kein Gas entweichen kann. Wenn der Behälter abgekühlt wird, wird das Gas im Inneren ebenfalls kälter und man beobachtet, dass sein Druck abnimmt. Da der Behälter starr und dicht verschlossen ist, bleiben sowohl das Volumen als auch die Anzahl der Gasmole konstant. Erhitzt man die Kugel, wird das Gas im Inneren heißer (Abbildung 2) und der Druck steigt an.

Abbildung 2. Die Auswirkung der Temperatur auf den Gasdruck: Wenn die Heizplatte ausgeschaltet ist, ist der Druck des Gases in der Kugel relativ niedrig. Wenn das Gas erwärmt wird, steigt der Druck des Gases in der Kugel.

Diese Beziehung zwischen Temperatur und Druck wird für jede Gasprobe beobachtet, die auf ein konstantes Volumen beschränkt ist. Ein Beispiel für experimentelle Druck-Temperatur-Daten ist in Abbildung 3 für eine Luftprobe unter diesen Bedingungen dargestellt. Es zeigt sich, dass Temperatur und Druck in einem linearen Verhältnis zueinander stehen, und wenn die Temperatur auf der Kelvin-Skala liegt, dann sind P und T direkt proportional (wiederum, wenn Volumen und Mole des Gases konstant gehalten werden); wenn die Temperatur auf der Kelvin-Skala um einen bestimmten Faktor ansteigt, steigt der Gasdruck um denselben Faktor.

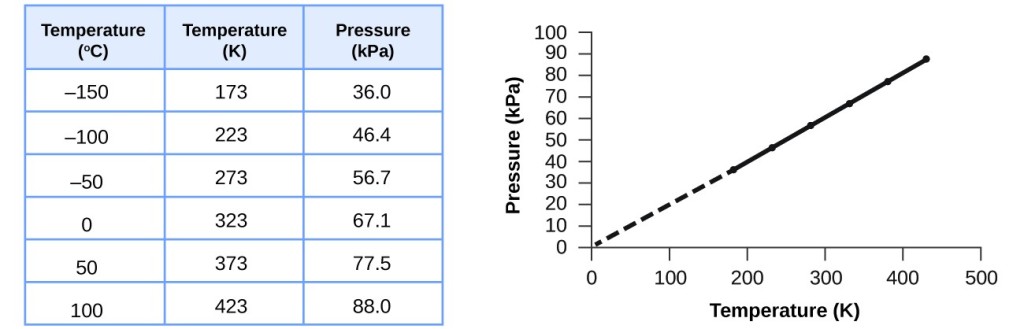
Abbildung 3. Für ein konstantes Volumen und eine konstante Luftmenge sind Druck und Temperatur direkt proportional, sofern die Temperatur in Kelvin angegeben wird. (Messungen bei niedrigeren Temperaturen sind wegen der Kondensation des Gases nicht möglich). Wenn diese Linie zu niedrigeren Drücken extrapoliert wird, erreicht sie einen Druck von 0 bei -273 °C, was 0 auf der Kelvinskala und die niedrigste mögliche Temperatur ist, die als absoluter Nullpunkt bezeichnet wird.

Guillaume Amontons war der erste, der die Beziehung zwischen dem Druck und der Temperatur eines Gases empirisch feststellte (~1700), und Joseph Louis Gay-Lussac bestimmte die Beziehung noch genauer (~1800). Aus diesem Grund ist die P-T-Beziehung für Gase entweder als Gay-Lussac-Gesetz oder als Amontons’sches Gesetz bekannt. Unter beiden Bezeichnungen besagt es, dass der Druck einer bestimmten Gasmenge direkt proportional zu seiner Temperatur auf der Kelvinskala ist, wenn das Volumen konstant gehalten wird. Mathematisch lässt sich dies folgendermaßen ausdrücken:

\large P\propto T

\large P=\text{constant}\times T

\large P=k\times T

wobei ∝ „ist proportional zu“ bedeutet, und k eine Proportionalitätskonstante ist, die von der Identität, der Menge und dem Volumen des Gases abhängt.

\large\frac{{P}_{1}}{{T}_{1}}=\frac{{P}_{2}}{{T}_{2}}

Diese Gleichung ist nützlich für Druck-Temperatur-Berechnungen für ein eingeschlossenes Gas mit konstantem Volumen. Beachten Sie, dass die Temperaturen für alle Gasgesetzberechnungen auf der Kelvinskala liegen müssen (0 auf der Kelvinskala und die niedrigste mögliche Temperatur wird als absoluter Nullpunkt bezeichnet). (Beachten Sie auch, dass es mindestens drei Möglichkeiten gibt, um zu beschreiben, wie sich der Druck eines Gases bei einer Temperaturänderung verändert: Wir können eine Wertetabelle, ein Diagramm oder eine mathematische Gleichung verwenden.)

Volumen und Temperatur: Charles’sches Gesetz

Wenn wir einen Ballon mit Luft füllen und ihn verschließen, enthält der Ballon eine bestimmte Menge Luft bei atmosphärischem Druck, sagen wir 1 atm. Legt man den Ballon in einen Kühlschrank, wird das Gas darin kalt und der Ballon schrumpft (obwohl sowohl die Gasmenge als auch der Druck konstant bleiben). Wenn wir den Ballon sehr kalt machen, schrumpft er stark und dehnt sich wieder aus, wenn er sich erwärmt.

Diese Beispiele für die Auswirkung der Temperatur auf das Volumen einer bestimmten Menge eines eingeschlossenen Gases bei konstantem Druck sind allgemein gültig: Das Volumen nimmt mit steigender Temperatur zu und mit sinkender Temperatur ab. Die Volumen-Temperatur-Daten für eine 1-Mol-Probe Methangas bei 1 atm sind in Abbildung 4 aufgeführt und grafisch dargestellt.

Abbildung 4. Das Volumen und die Temperatur sind für 1 Mol Methangas bei einem konstanten Druck von 1 atm linear miteinander verbunden. Wenn die Temperatur in Kelvin angegeben wird, sind Volumen und Temperatur direkt proportional. Die Linie stoppt bei 111 K, weil sich Methan bei dieser Temperatur verflüssigt; bei der Extrapolation schneidet sie den Ursprung des Diagramms, was einer Temperatur von absolut Null entspricht.

Die Beziehung zwischen dem Volumen und der Temperatur einer bestimmten Gasmenge bei konstantem Druck ist als Charles’sches Gesetz bekannt, in Anerkennung des französischen Wissenschaftlers und Ballonflugpioniers Jacques Alexandre César Charles. Das Charles’sche Gesetz besagt, dass das Volumen einer bestimmten Gasmenge bei konstantem Druck direkt proportional zu seiner Temperatur auf der Kelvinskala ist.

Mathematisch kann dies wie folgt geschrieben werden:

\groß V\propto T

\groß V=\text{constant}\cdot T

\groß V=k\cdot T

mit k als Proportionalitätskonstante, die von der Menge und dem Druck des Gases abhängt.

\large\frac{{V}_{1}}{{T}_{1}}=\frac{{V}_{2}}{{T}_{2}}

Volumen und Druck: Boyle’s Law

Wenn wir eine luftdichte Spritze teilweise mit Luft füllen, enthält die Spritze eine bestimmte Menge Luft bei konstanter Temperatur, sagen wir 25 °C. Wenn wir den Kolben langsam eindrücken und dabei die Temperatur konstant halten, wird das Gas in der Spritze auf ein kleineres Volumen komprimiert und der Druck nimmt zu; wenn wir den Kolben herausziehen, vergrößert sich das Volumen und der Druck nimmt ab. Dieses Beispiel für die Auswirkung des Volumens auf den Druck einer bestimmten Menge eines eingeschlossenen Gases ist allgemein gültig. Eine Verringerung des Volumens eines eingeschlossenen Gases erhöht seinen Druck, und eine Vergrößerung des Volumens verringert seinen Druck. Vergrößert sich das Volumen um einen bestimmten Faktor, sinkt der Druck um denselben Faktor und umgekehrt. Die Volumen-Druck-Daten einer Luftprobe bei Raumtemperatur sind in Abbildung 5 grafisch dargestellt.

Abbildung 5. Wenn ein Gas ein kleineres Volumen einnimmt, übt es einen höheren Druck aus; wenn es ein größeres Volumen einnimmt, übt es einen niedrigeren Druck aus (vorausgesetzt, die Gasmenge und die Temperatur ändern sich nicht). Da P und V umgekehrt proportional sind, ist ein Graph von 1/P gegen V linear.

Im Gegensatz zu den Beziehungen P-T und V-T sind Druck und Volumen nicht direkt proportional zueinander. Stattdessen weisen P und V eine umgekehrte Proportionalität auf: Eine Erhöhung des Drucks führt zu einer Verringerung des Volumens des Gases. Mathematisch lässt sich dies folgendermaßen ausdrücken:

groß P\propto 1\text{/}V\text{ oder }P=k\cdot 1\text{/}V\text{ oder }P\cdot V=k\text{ oder }{P}_{1}{V}_{1}={P}_{2}{V}_{2}

mit k als Konstante. Grafisch wird diese Beziehung durch die gerade Linie dargestellt, die sich ergibt, wenn man den Kehrwert des Drucks \large\left(\frac{1}{P}\right) gegen das Volumen (V) aufträgt, oder den Kehrwert des Volumens \large\left(\frac{1}{V}\right) gegen den Druck (V). Diagramme mit gekrümmten Linien sind bei niedrigen oder hohen Werten der Variablen schwer genau abzulesen, und sie sind schwieriger für die Anpassung theoretischer Gleichungen und Parameter an experimentelle Daten zu verwenden. Aus diesen Gründen versuchen Wissenschaftler oft, einen Weg zu finden, ihre Daten zu „linearisieren“. Wenn man P gegen V aufträgt, erhält man eine Hyperbel (siehe Abbildung 6).

Die Beziehung zwischen dem Volumen und dem Druck einer bestimmten Gasmenge bei konstanter Temperatur wurde erstmals vor über 300 Jahren von dem englischen Naturphilosophen Robert Boyle veröffentlicht. Sie ist in der Aussage zusammengefasst, die heute als Boyle’sches Gesetz bekannt ist: Das Volumen einer bestimmten Gasmenge bei konstanter Temperatur ist umgekehrt proportional zu dem Druck, unter dem es gemessen wird.

Chemie in Aktion: Atmung und das Boyle’sche Gesetz

Was tun Sie etwa 20 Mal pro Minute, Ihr ganzes Leben lang, ohne Unterbrechung und oft, ohne sich dessen überhaupt bewusst zu sein? Die Antwort ist natürlich die Atmung oder das Atmen. Wie funktioniert sie? Es stellt sich heraus, dass hier die Gasgesetze gelten. Die Lunge nimmt Gas auf, das der Körper braucht (Sauerstoff), und gibt Abfallgase ab (Kohlendioxid). Die Lunge besteht aus schwammigem, dehnbarem Gewebe, das sich beim Atmen ausdehnt und zusammenzieht. Beim Einatmen ziehen sich das Zwerchfell und die Zwischenrippenmuskeln (die Muskeln zwischen den Rippen) zusammen, wodurch sich der Brustraum ausdehnt und das Lungenvolumen vergrößert wird. Die Vergrößerung des Volumens führt zu einem Druckabfall (Boyle’sches Gesetz). Dies führt dazu, dass Luft in die Lunge strömt (von hohem Druck zu niedrigem Druck). Wenn Sie ausatmen, kehrt sich der Prozess um: Ihr Zwerchfell und Ihre Rippenmuskeln entspannen sich, Ihr Brustkorb zieht sich zusammen und Ihr Lungenvolumen nimmt ab, wodurch der Druck wieder steigt (Boyle’sches Gesetz) und Luft aus der Lunge strömt (von hohem Druck zu niedrigem Druck). Sie atmen dann wieder ein und aus und wiederholen diesen Zyklus nach dem Boyle’schen Gesetz für den Rest Ihres Lebens (Abbildung 7).

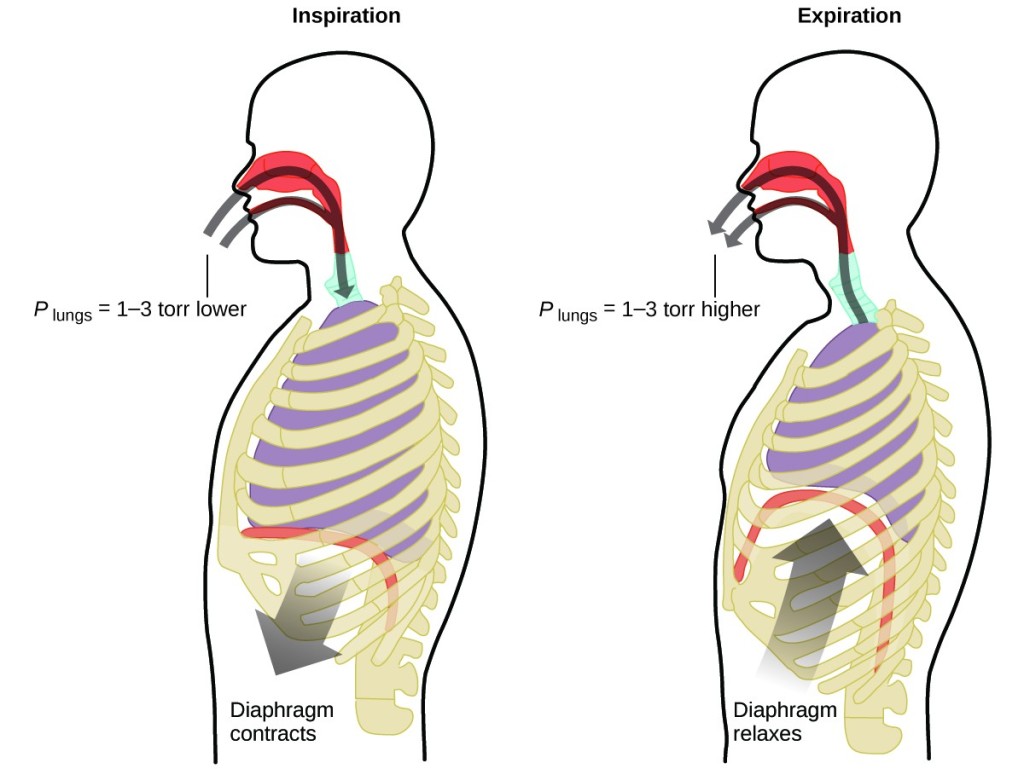
Abbildung 7. Die Atmung erfolgt, weil durch das Ausdehnen und Zusammenziehen des Lungenvolumens kleine Druckunterschiede zwischen den Lungen und der Umgebung entstehen, wodurch Luft in die Lungen gesaugt und aus ihnen herausgedrückt wird.

Mol Gas und Volumen: Avogadrosches Gesetz

Der italienische Wissenschaftler Amedeo Avogadro stellte 1811 eine Hypothese auf, um das Verhalten von Gasen zu erklären, die besagt, dass gleiche Volumina aller Gase, die unter den gleichen Temperatur- und Druckbedingungen gemessen werden, die gleiche Anzahl von Molekülen enthalten. Im Laufe der Zeit wurde diese Beziehung durch zahlreiche experimentelle Beobachtungen gestützt und durch das Avogadrosche Gesetz ausgedrückt: Bei einem eingeschlossenen Gas sind das Volumen (V) und die Anzahl der Mole (n) direkt proportional, wenn Druck und Temperatur konstant bleiben.

In Gleichungsform wird dies geschrieben als:

\large\begin{array}{ccccc}V\propto n& \text{oder}& V=k\times n& \text{oder}& \frac{{V}_{1}}{{n}_{1}}=\frac{{V}_{2}}{{n}_{2}}\end{array}

Mathematische Beziehungen lassen sich auch für die anderen Variablenpaare bestimmen, wie z. B. P gegen n und n gegen T.

Glossar

Absoluter Nullpunkt: Temperatur, bei der das Volumen eines Gases nach dem Charles’schen Gesetz gleich Null wäre.

Avogadrosches Gesetz: Volumen eines Gases bei konstanter Temperatur und konstantem Druck ist proportional zur Anzahl der Gasmoleküle

Boylesches Gesetz: Volumen einer bestimmten Anzahl von Molen eines Gases bei konstanter Temperatur ist umgekehrt proportional zum Druck, unter dem es gemessen wird

Charlessches Gesetz: Das Volumen einer gegebenen Anzahl von Molen eines Gases ist direkt proportional zu seiner Kelvin-Temperatur, wenn der Druck konstant gehalten wird

Gay-Lussac’s law: (auch Amontons’sches Gesetz): Der Druck einer gegebenen Anzahl von Molen eines Gases ist direkt proportional zu seiner Kelvin-Temperatur, wenn das Volumen konstant gehalten wird