Ein wachsender Bereich von Interesse für Wissenschaftler, die Bedeutung, Macht oder Einfluss zwischen Entitäten erforschen, ist die sogenannte Graphentheorie. Die Wurzeln der Graphentheorie gehen auf das Jahr 1736 zurück, als der Mathematiker Carl Ehler Leonhard Euler das Problem der Königsberger Brücken vorstellte.
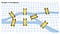
Das Problem der Königsberger Brücken geht auf die ehemalige deutsche Stadt Königsberg zurück, die auf beiden Seiten des Flusses Pregel liegt. In der Mitte befanden sich zwei große Inseln, die durch sieben Brücken miteinander und mit den Flussufern verbunden waren. Carl Ehler war besessen davon, einen Weg zu finden, auf dem er jede der sieben Brücken durchqueren konnte, ohne eine von ihnen mehr als einmal zu überqueren. Ehler wandte sich an Leonhard Euler, einen Schweizer Mathematiker. Euler bestätigte Ehlers Hypothese, dass es für das Problem keine Lösung gab, und Eulers Erklärung bildete die Grundlage für ein neues mathematisches Paradigma namens Positionsgeometrie.
Eulers neues Geometrie-Paradigma besagt, dass die Lage der Brücken keine Rolle spielt. Das Problem kann stattdessen vereinfacht werden, indem man jede Brücke in einen Punkt (Knoten) mit Linien (Kanten) verwandelt, die die Verbindungen zwischen ihnen darstellen. Diese Praxis der Verwendung von Knoten und Kanten ist heute als Graphentheorie bekannt.
Sie können hier mehr über das Problem der Brücken in Königsberg lesen.
Anfänglich war die Graphentheorie für die Problemlösung nicht sehr nützlich und wurde von Mathematikern nicht sehr geschätzt. Mit der modernen Rechenleistung zur Verarbeitung großer Permutationen sind die Prinzipien der Graphentheorie jedoch praktischer geworden. In diesem Artikel lernen Sie, die Prinzipien der Graphentheorie auf Python-basierte Analysen anzuwenden.


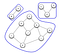
Nicht alle Netzwerke in einem Graphensystem sind miteinander verbunden. Diese Unterbrechung tritt auf, wenn Komponenten gebildet werden. Wie im folgenden Graphen gezeigt, wird eine Komponente nur dann gebildet, wenn jeder Knoten einen Pfad zu anderen Knoten hat.
Angewandte Graphentheorie in Python
In Python wird networkx oft für die angewandte Graphentheorie, auch bekannt als Netzwerkanalyse, verwendet. Das Paket hat nützliche Funktionen, um die Eigenschaften eines Graphen schnell zusammenzufassen. Schauen Sie sich die folgenden Schritte an und folgen Sie uns, um einen Graphen zu erstellen und seinen Aufbau zu verstehen.
Der folgende Code erstellt zunächst ein leeres Graphenobjekt P. Die nächsten Schritte fügen Knoten hinzu und beschreiben die Kanten.
Argumente wie <object>.nodes() oder <object>.edges() sind schnelle Wege, um alle Knoten und Kanten des Graphsystems zu sehen.
print(P.nodes())print(P.edges())
Schließlich wird nx.draw verwendet, um das Netzwerk zu visualisieren.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
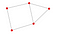
Übungen 1:
Nachdem die grundlegenden Konzepte von Graphen besprochen wurden, sind die folgenden Übungen eine gute Methode zum Üben:
- Wie viele Knoten sind in dem obigen Graphen?
- Wie viele Kanten gibt es im obigen Graphen?
- Wie lautet die Geodäte für E und C?
- Gibt es mehr als eine Komponente im Graphen?
Verwendung realer Daten
Die folgende Übung verwendet Daten für Flüge innerhalb der Vereinigten Staaten im Jahr 2015. Der Datensatz enthält Start- und Zielflughäfen sowie Attribute, die den Flug beschreiben, einschließlich Flugzeit und Verspätungen (wetter-, sicherheits- oder fluglinienbedingt).
Da der Datensatz sehr umfangreich ist, wird sich die Übung auf Flüge konzentrieren, die von Flughäfen im Großraum Los Angeles ausgehen (Los Angeles (LAX), Burbank (BUR), Orange County (SNA) und San Bernardino County (ONT)). Außerdem werden wir uns auf Flüge konzentrieren, die meinem Deloitte-Reiseplan ähneln – sonntags abfliegen und donnerstags zurückkehren.
Da wir bereits über Abflug- und Zieldaten verfügen, werden die Felder **** ORIGIN_AIRPORT und DESTINATION_AIRPORT als Quellfelder für Knoten und Kanten dienen – es ist nicht notwendig, Knoten oder Kanten zu erstellen, wie wir es in der ersten Übung getan haben. Sobald die Knoten definiert sind, liefert <object>.edges() alle paarweisen Beziehungen zwischen ihnen. Schließlich hilft nx.draw bei der Erstellung eines Graphen für die Kanten.

FG.edges()

nx.draw(FG, with_labels = True)

In der obigen Ausgabe, sind die Knoten mit den Flughafencodes beschriftet. Alle Kanten führen zu einem der vier Flughäfen im Großraum Los Angeles, da nur diese vier für diese Übung ausgewählt wurden. Los Angeles International (LAX) ist der größte der vier Flughäfen, und das Diagramm zeigt deutlich, dass viele Städte nur über LAX und nicht über andere kleinere Flughäfen erreichbar sind. Dies verdeutlicht die Verbundenheit oder Gradzentralität von LAX. In networkx wird nx.algorithms.degree_centrality(<object>) **** verwendet, um die Zentralität jedes Knotens im Graphsystem zu ermitteln.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
Wir können noch weiter gehen und eine kurze „for-Schleife“ verwenden, um Kanten zwischen zwei Bereichen von Interesse zu erzeugen. Zum Beispiel wird der folgende Code verwendet, um alle möglichen Flüge von San Bernardino County (ONT) nach Newark (EWR) entweder am Sonntag oder am Donnerstag zu finden.
Aus den verschiedenen Flugoptionen zwischen San Bernardino County und Newark kann nx.dijkstra_path verwendet werden, um den euklidischen Pfad (oder den kürzesten Pfad) zu finden.
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
Übungen 2:
- Erstellen Sie den folgenden Graphen mit
nx.draw(). Hinweis: Ihr Netzwerk sieht vielleicht nicht genau so aus, aber die Pfade, Kanten und Knoten sollten mit dem untenstehenden Netzwerk übereinstimmen. - Drucken Sie alle Kanten.
- Was ist der kürzeste Pfad von L nach F?
