Über 90 % der natürlich vorkommenden und vom Menschen hergestellten Feststoffe sind kristallin. Die meisten Feststoffe bilden sich mit einer regelmäßigen Anordnung ihrer Teilchen, weil die gesamten anziehenden Wechselwirkungen zwischen den Teilchen maximiert werden und die gesamte intermolekulare Energie minimiert wird, wenn die Teilchen auf die effizienteste Weise gepackt werden. Die regelmäßige Anordnung auf atomarer Ebene spiegelt sich oft auch auf makroskopischer Ebene wider. In diesem Modul werden wir einige Details über die Strukturen von metallischen und ionischen kristallinen Festkörpern erforschen und lernen, wie diese Strukturen experimentell bestimmt werden.

Die Strukturen von Metallen

Wir beginnen unsere Diskussion über kristalline Festkörper mit der Betrachtung von elementaren Metallen, die relativ einfach sind, weil sie nur eine Art von Atom enthalten. Ein reines Metall ist ein kristalliner Festkörper, bei dem die Metallatome in einem sich wiederholenden Muster dicht aneinander gepackt sind. Einige der Eigenschaften von Metallen im Allgemeinen, wie z. B. ihre Verformbarkeit und Duktilität, sind weitgehend darauf zurückzuführen, dass die gleichen Atome in einem regelmäßigen Muster angeordnet sind. Die unterschiedlichen Eigenschaften eines Metalls im Vergleich zu einem anderen hängen teilweise von der Größe der Atome und den Besonderheiten ihrer räumlichen Anordnung ab. In den folgenden Abschnitten werden wir die Gemeinsamkeiten und Unterschiede der vier häufigsten Kristallgeometrien von Metallen untersuchen.

Einheitszellen von Metallen

Die Struktur eines kristallinen Festkörpers, ob Metall oder nicht, lässt sich am besten beschreiben, wenn man seine einfachste sich wiederholende Einheit betrachtet, die als Einheitszelle bezeichnet wird. Die Einheitszelle besteht aus Gitterpunkten, die die Positionen der Atome oder Ionen darstellen. Die gesamte Struktur besteht dann aus dieser Einheitszelle, die sich in drei Dimensionen wiederholt, wie in Abbildung 1 dargestellt.

Abbildung 1. Eine Einheitszelle zeigt die Lage der Gitterpunkte, die sich in alle Richtungen wiederholen.

Lassen Sie uns unsere Untersuchung der Kristallgitterstruktur und der Einheitszellen mit der einfachsten Struktur und der grundlegendsten Einheitszelle beginnen. Um dies zu veranschaulichen, stellen Sie sich vor, Sie nehmen eine große Anzahl identischer Kugeln, wie z.B. Tennisbälle, und ordnen sie gleichmäßig in einem Behälter an. Die einfachste Art, dies zu tun, besteht darin, Schichten zu bilden, in denen die Kugeln einer Schicht direkt über denen der darunter liegenden Schicht liegen, wie in Abbildung 2 dargestellt. Diese Anordnung wird als einfache kubische Struktur bezeichnet, und die Einheitszelle wird als einfache kubische Einheitszelle oder primitive kubische Einheitszelle bezeichnet.

Abbildung 2. Wenn Metallatome so angeordnet sind, dass die Kugeln in einer Schicht direkt über oder unter den Kugeln in einer anderen Schicht liegen, wird die Gitterstruktur als einfach kubisch bezeichnet. Man beachte, dass sich die Kugeln berühren.

In einer einfachen kubischen Struktur sind die Kugeln nicht so dicht gepackt, wie sie sein könnten, und sie „füllen“ nur etwa 52 % des Volumens des Behälters. Dies ist eine relativ ineffiziente Anordnung, und nur ein Metall (Polonium, Po) kristallisiert in einer einfachen kubischen Struktur. Wie in Abbildung 3 dargestellt, besteht ein Festkörper mit dieser Art der Anordnung aus Ebenen (oder Schichten), in denen jedes Atom nur mit den vier nächsten Nachbarn in seiner Schicht in Kontakt steht, mit einem Atom direkt über ihm in der Schicht darüber und mit einem Atom direkt unter ihm in der Schicht darunter. Die Anzahl der anderen Teilchen, die jedes Teilchen in einem kristallinen Festkörper berührt, wird als Koordinationszahl bezeichnet. Für ein Poloniumatom in einer einfachen kubischen Anordnung beträgt die Koordinationszahl also sechs.

Abbildung 3. Ein Atom in einer einfachen kubischen Gitterstruktur berührt sechs andere Atome und hat daher eine Koordinationszahl von sechs.

In einem einfachen kubischen Gitter ist die Einheitszelle, die sich in alle Richtungen wiederholt, ein Würfel, der durch die Zentren von acht Atomen definiert ist, wie in Abbildung 4 dargestellt. Die Atome an den benachbarten Ecken dieser Einheitszelle berühren sich gegenseitig, so dass die Kantenlänge dieser Zelle zwei Atomradien oder einem Atomdurchmesser entspricht. Eine kubische Einheitszelle enthält nur die Teile dieser Atome, die sich innerhalb der Zelle befinden. Da ein Atom in einer Ecke einer einfachen kubischen Elementarzelle von insgesamt acht Elementarzellen eingeschlossen wird, befindet sich nur ein Achtel dieses Atoms innerhalb einer bestimmten Elementarzelle. Und da jede einfache kubische Einheitszelle ein Atom an jeder ihrer acht „Ecken“ hat, gibt es 8 \mal \frac{1}{8}=1 Atom innerhalb einer einfachen kubischen Einheitszelle.

Abbildung 4. Eine einfache kubische Gittereinheit enthält an jeder ihrer acht Ecken ein Achtel eines Atoms, so dass sie insgesamt ein Atom enthält.

Beispiel 1: Berechnung von Atomradius und Dichte für Metalle, Teil 1

Die Kantenlänge der Einheitszelle von Alpha-Polonium beträgt 336 pm.

1. Bestimmen Sie den Radius eines Poloniumatoms.
2. Bestimmen Sie die Dichte von Alpha-Polonium.

Lösung anzeigen

Alpha-Polonium kristallisiert in einer einfachen kubischen Einheitszelle:

1. Zwei benachbarte Po-Atome berühren sich, also ist die Kantenlänge dieser Zelle gleich zwei Po-Atomradien: l=2r. Daher ist der Radius von Po r=\dfrac{\text{l}}{2}=\dfrac{\text{336 pm}}{2}=\text{168 pm}.
2. Die Dichte ist gegeben durch \text{Dichte}=\dfrac{\text{Masse}}{\text{Volumen}}. Die Dichte von Polonium kann durch Bestimmung der Dichte seiner Einheitszelle (die in einer Einheitszelle enthaltene Masse geteilt durch das Volumen der Einheitszelle) ermittelt werden. Da eine Po-Einheitszelle an jeder ihrer acht Ecken ein Achtel eines Po-Atoms enthält, enthält eine Einheitszelle ein Po-Atom.

Die Masse einer Po-Einheitszelle kann ermittelt werden durch:

\text{1 Po-Einheitszelle}\times \dfrac{\text{1 Po-Atom}}{\text{1 Po-Einheitszelle}}\times \dfrac{\text{1 mol Po}}{6.022\times {10}^{23}\text{Po-Atome}}\times \dfrac{208.998\text{g}}{\text{1 mol Po}}=3.47\times {10}^{-22}\text{g}

Das Volumen einer Po-Einheitszelle kann wie folgt berechnet werden:

V={l}^{3}={(336\times {10}^{-10}\text{cm})}^{3}=3.79\times {10}^{-23}{\text{cm}}^{3}

(Man beachte, dass die Kantenlänge von pm in cm umgerechnet wurde, um die üblichen Volumeneinheiten für die Dichte zu erhalten.)

Daher ist die Dichte von \text{Po}=\dfrac{3.471\mal {10}^{-22}\text{g}}{3.79\mal {10}^{-23}{\text{cm}}^{3}}={\text{9.16 g/cm}^{3}

Kontrolliere dein Wissen

Die Kantenlänge der Einheitszelle für Nickel beträgt 0.3524 nm. Die Dichte von Ni beträgt 8,90 g/cm3. Kristallisiert Nickel in einer einfachen kubischen Struktur? Erkläre.

Zeige Lösung

Nein. Wenn Ni einfach kubisch wäre, wäre seine Dichte gegeben durch:

\text{1 Ni-Atom}\times \dfrac{\text{1 mol Ni}}{6.022\times {10}^{23}\text{Ni atoms}}\times \dfrac{58.693\text{g}}{\text{1 mol Ni}}=9.746\times {10}^{-23}\text{g}
V={l}^{3}={(3.524\times {10}^{-8}\text{cm})}^{3}=4.376\times {10}^{-23}{\text{cm}}^{3}

Dann wäre die Dichte von Ni =\dfrac{9.746\times {10}^{-23}\text{g}}{4.376\times {10}^{-23}{\text{cm}}^{3}}={text{2.23 g/cm}}^{3}

Da die tatsächliche Dichte von Ni nicht annähernd so hoch ist, bildet Ni keine einfache kubische Struktur.

Die meisten Metallkristalle sind einer der vier Haupttypen von Einheitszellen. Im Moment konzentrieren wir uns auf die drei kubischen Einheitszellen: die einfache kubische (die wir bereits gesehen haben), die körperzentrierte kubische Einheitszelle und die flächenzentrierte kubische Einheitszelle, die alle in Abbildung 5 dargestellt sind. (Man beachte, dass es tatsächlich sieben verschiedene Gittersysteme gibt, von denen einige mehr als eine Art von Gitter haben, was insgesamt 14 verschiedene Arten von Einheitszellen ergibt. Die komplizierteren Geometrien werden erst später in diesem Modul behandelt.)

Abbildung 5. Kubische Einheitszellen von Metallen zeigen (in den oberen Abbildungen) die Lage der Gitterpunkte und (in den unteren Abbildungen) die in der Einheitszelle befindlichen Metallatome.

Einige Metalle kristallisieren in einer Anordnung, die eine kubische Einheitszelle mit Atomen an allen Ecken und einem Atom in der Mitte aufweist, wie in Abbildung 6 dargestellt. Dies nennt man einen kubisch-raumzentrierten Festkörper (BCC). Die Atome in den Ecken einer BCC-Einheitszelle berühren sich nicht gegenseitig, sondern berühren das Atom in der Mitte. Eine BCC-Einheitszelle enthält zwei Atome: ein Achtel eines Atoms an jeder der acht Ecken ( 8\mal \frac{1}{8}=1 Atom aus den Ecken) plus ein Atom aus dem Zentrum. Jedes Atom in dieser Struktur berührt vier Atome in der Schicht über ihm und vier Atome in der Schicht unter ihm. Somit hat ein Atom in einer BCC-Struktur eine Koordinationszahl von acht.

Abbildung 6. In einer kubisch-raumzentrierten Struktur berühren sich die Atome in einer bestimmten Schicht nicht gegenseitig. Jedes Atom berührt vier Atome in der Schicht über ihm und vier Atome in der Schicht unter ihm.

Atome in BCC-Anordnungen sind viel effizienter gepackt als in einer einfachen kubischen Struktur und nehmen etwa 68 % des Gesamtvolumens ein. Zu den isomorphen Metallen mit einer BCC-Struktur gehören K, Ba, Cr, Mo, W und Fe bei Raumtemperatur. (Elemente oder Verbindungen, die mit der gleichen Struktur kristallisieren, werden als isomorph bezeichnet.)

Viele andere Metalle, wie Aluminium, Kupfer und Blei, kristallisieren in einer Anordnung, die eine kubische Einheitszelle mit Atomen an allen Ecken und in den Zentren jeder Fläche aufweist, wie in Abbildung 7 dargestellt. Diese Anordnung wird als kubisch-flächenzentrierter Festkörper (FCC) bezeichnet. Eine FCC-Einheitszelle enthält vier Atome: ein Achtel eines Atoms an jeder der acht Ecken ( 8\mal \frac{1}{8}=1 Atom von den Ecken) und die Hälfte eines Atoms auf jeder der sechs Flächen (6\mal \frac{1}{2}=3 Atome von den Flächen). Die Atome an den Ecken berühren die Atome in den Zentren der benachbarten Flächen entlang der Flächendiagonalen des Würfels. Da sich die Atome auf identischen Gitterpunkten befinden, haben sie identische Umgebungen.

Abbildung 7. Ein kubisch flächenzentrierter Festkörper hat Atome an den Ecken und, wie der Name schon sagt, in den Zentren der Flächen seiner Einheitszellen.

Atome in einer FCC-Anordnung sind so eng wie möglich zusammen gepackt, wobei die Atome 74 % des Volumens einnehmen. Diese Struktur wird auch als kubisch dichteste Packung (CCP) bezeichnet. Bei CCP gibt es drei sich wiederholende Schichten von hexagonal angeordneten Atomen. Jedes Atom berührt sechs Atome in seiner eigenen Schicht, drei in der Schicht darüber und drei in der Schicht darunter. In dieser Anordnung berührt jedes Atom 12 nahe Nachbarn und hat daher eine Koordinationszahl von 12. Die Tatsache, dass FCC- und CCP-Anordnungen gleichwertig sind, ist vielleicht nicht sofort ersichtlich, aber warum sie tatsächlich dieselbe Struktur sind, wird in Abbildung 8 veranschaulicht.

Abbildung 8 gekennzeichnet sind. Eine CCP-Anordnung besteht aus drei sich wiederholenden Schichten (ABCABC…) von sechseckig angeordneten Atomen. Atome in einer CCP-Struktur haben eine Koordinationszahl von 12, weil sie sechs Atome in ihrer Schicht berühren, plus drei Atome in der Schicht darüber und drei Atome in der Schicht darunter. Dreht man die Perspektive, sieht man, dass eine CCP-Struktur eine Einheitszelle mit einer Fläche hat, die an einer Ecke ein Atom der Schicht A, über eine Diagonale (an zwei Ecken und in der Mitte der Fläche) Atome der Schicht B und an der verbleibenden Ecke ein Atom der Schicht C enthält. Dies entspricht einer kubisch-flächenzentrierten Anordnung.

Da die engste Packung die Gesamtanziehung zwischen den Atomen maximiert und die gesamte intermolekulare Energie minimiert, packen die Atome in den meisten Metallen auf diese Weise. In einfachen metallischen Kristallstrukturen finden wir zwei Arten von dichter Packung: CCP, dem wir bereits begegnet sind, und die hexagonal dichteste Packung (HCP), die in Abbildung 9 dargestellt ist. Beide bestehen aus sich wiederholenden Schichten von hexagonal angeordneten Atomen. In beiden Fällen wird eine zweite Schicht (B) auf die erste Schicht (A) gelegt, so dass jedes Atom der zweiten Schicht mit drei Atomen der ersten Schicht in Kontakt steht. Die dritte Schicht kann auf eine von zwei Arten angeordnet werden. Bei HCP liegen die Atome der dritten Schicht direkt über den Atomen der ersten Schicht (d. h. die dritte Schicht ist ebenfalls vom Typ A), und die Stapelung besteht aus abwechselnd dicht gepackten Schichten vom Typ A und B (d. h. ABABAB⋯). Bei CCP liegen die Atome der dritten Schicht nicht über den Atomen der ersten beiden Schichten (d. h. die dritte Schicht ist vom Typ C), und die Stapelung besteht aus abwechselnd dicht gepackten Schichten vom Typ A, Typ B und Typ C (d. h. ABCABCABC⋯). Etwa zwei Drittel aller Metalle kristallisieren in engst gepackten Anordnungen mit Koordinationszahlen von 12. Zu den Metallen, die in einer HCP-Struktur kristallisieren, gehören Cd, Co, Li, Mg, Na und Zn, und zu den Metallen, die in einer CCP-Struktur kristallisieren, gehören Ag, Al, Ca, Cu, Ni, Pb und Pt.

Abbildung 9 beschriftet. Bei beiden Arten der dichtesten Packung sind die Atome so kompakt wie möglich gepackt. Die hexagonale dichteste Packung besteht aus zwei alternierenden Schichten (ABABAB…). Die kubische dichteste Packung besteht aus drei abwechselnden Schichten (ABCABCABC…).

Beispiel 2: Berechnung von Atomradius und Dichte für Metalle, Teil 2

Calcium kristallisiert in einer kubisch-flächenzentrierten Struktur. Die Kantenlänge der Einheitszelle beträgt 558,8 pm.

1. Wie groß ist der Atomradius von Ca in dieser Struktur?
2. Berechnen Sie die Dichte von Ca.

Lösung anzeigen

Teil 1

In einer FCC-Struktur berühren sich die Ca-Atome über die Diagonale der Fläche, so dass die Länge der Diagonale vier Ca-Atomradien (d = 4r) entspricht. Zwei benachbarte Kanten und die Diagonale der Fläche bilden ein rechtwinkliges Dreieck, wobei die Länge jeder Seite gleich 558,8 pm und die Länge der Hypotenuse gleich vier Ca-Atomradien ist:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}\longrightarrow {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}}{16}}=\text{197.6 pmg für einen Ca-Radius}.

Teil 2

Die Dichte ist gegeben durch \text{Dichte}=\dfrac{\text{Masse}}{\text{Volumen}}. Die Dichte von Kalzium kann durch Bestimmung der Dichte seiner Einheitszelle ermittelt werden: z. B. die in einer Einheitszelle enthaltene Masse geteilt durch das Volumen der Einheitszelle. Eine flächenzentrierte Ca-Einheitszelle hat ein Achtel eines Atoms an jeder der acht Ecken \left(8\mal \dfrac{1}{8}=1\text{Atom}\right) und ein halbes Atom auf jeder der sechs Flächen \left(6\mal \dfrac{1}{2}=3\text{Atome}\right), also insgesamt vier Atome in der Einheitszelle.

Die Masse der Einheitszelle lässt sich ermitteln durch:

\text{1 Ca-Einheitszelle}\times \dfrac{\text{4 Ca-Atome}}{\text{1 Ca-Einheitszelle}}\times \dfrac{\text{1 mol Ca}}{6.022\times {10}^{23}\text{Ca-Atome}}\times \dfrac{40.078\text{g}}{\text{1 mol Ca}}=2.662\times {10}^{-22}\text{g}

Das Volumen einer Ca-Einheitszelle kann wie folgt berechnet werden:

V={a}^{3}={(558.8\times {10}^{-10}\text{cm})}^{3}=1.745\times {10}^{-22}{\text{cm}}^{3}

(Man beachte, dass die Kantenlänge von pm in cm umgerechnet wurde, um die üblichen Volumeneinheiten für die Dichte zu erhalten.)

Dann ist die Dichte von \text{Ca}=\dfrac{2.662\times {10}^{-22}\text{g}}{1.745\times {10}^{-22}{\text{cm}}^{3}}={\text{1.53 g/cm}}^{3}

Kontrolliere dein Wissen

Silber kristallisiert in einer FCC-Struktur. Die Kantenlänge der Einheitszelle beträgt 409 pm.

1. Wie groß ist der Atomradius von Ag in dieser Struktur?
2. Berechnen Sie die Dichte von Ag.

Lösungen anzeigen

1. 144 pm
2. 10.5 g/cm3

Im Allgemeinen wird eine Einheitszelle durch die Längen von drei Achsen (a, b und c) und die Winkel (α, β und γ) zwischen ihnen definiert, wie in Abbildung 10 dargestellt. Die Achsen sind definiert als die Längen zwischen Punkten im Raumgitter. Folglich verbinden die Achsen der Einheitszellen Punkte mit identischen Umgebungen.

Abbildung 10. Eine Einheitszelle ist durch die Längen ihrer drei Achsen (a, b und c) und die Winkel (α, β und γ) zwischen den Achsen definiert.

Es gibt sieben verschiedene Gittersysteme, von denen einige mehr als einen Gittertyp haben, also insgesamt vierzehn verschiedene Einheitszellen, die die in Abbildung 11 gezeigten Formen haben.

Abbildung 11. Es gibt sieben verschiedene Gittersysteme und 14 verschiedene Einheitszellen.

Die Strukturen von Ionenkristallen

Ionenkristalle bestehen aus zwei oder mehr verschiedenen Arten von Ionen, die in der Regel unterschiedliche Größen haben. Die Anordnung dieser Ionen in einer Kristallstruktur ist komplexer als die Anordnung von Metallatomen gleicher Größe.

Die meisten einatomigen Ionen verhalten sich wie geladene Kugeln, und ihre Anziehungskraft auf Ionen mit entgegengesetzter Ladung ist in jeder Richtung gleich groß. Folglich ergeben sich stabile Strukturen für ionische Verbindungen, (1) wenn Ionen einer Ladung von möglichst vielen Ionen der entgegengesetzten Ladung umgeben sind und (2) wenn die Kationen und Anionen miteinander in Kontakt sind. Die Strukturen werden von zwei Hauptfaktoren bestimmt: der relativen Größe der Ionen und dem Verhältnis der Anzahl positiver und negativer Ionen in der Verbindung.

Abbildung 12 beschriftet. Kationen können zwei Arten von Löchern zwischen den Anionen besetzen: oktaedrische Löcher oder tetraedrische Löcher.

In einfachen Ionenstrukturen sind die Anionen, die normalerweise größer als die Kationen sind, normalerweise in einer dicht gepackten Anordnung angeordnet. (Wie wir bereits gesehen haben, machen zusätzliche Elektronen, die vom selben Kern angezogen werden, die Anionen größer und weniger Elektronen, die vom selben Kern angezogen werden, die Kationen kleiner im Vergleich zu den Atomen, aus denen sie gebildet werden). Die kleineren Kationen besetzen in der Regel eine von zwei Arten von Löchern (oder Zwischenräumen), die zwischen den Anionen verbleiben. Das kleinere der beiden Löcher befindet sich zwischen drei Anionen in einer Ebene und einem Anion in einer benachbarten Ebene. Die vier Anionen, die dieses Loch umgeben, sind an den Ecken eines Tetraeders angeordnet, weshalb das Loch als Tetraederloch bezeichnet wird. Die größere Art von Loch befindet sich im Zentrum von sechs Anionen (drei in einer Ebene und drei in einer angrenzenden Ebene), die sich an den Ecken eines Oktaeders befinden; dies wird als oktaedrisches Loch bezeichnet. Abbildung 12 zeigt diese beiden Arten von Löchern.

Abhängig von der relativen Größe der Kationen und Anionen können die Kationen einer ionischen Verbindung tetraedrische oder oktaedrische Löcher besetzen, wie in Abbildung 13 dargestellt. Relativ kleine Kationen besetzen tetraedrische Löcher, und größere Kationen besetzen oktaedrische Löcher. Wenn die Kationen zu groß sind, um in die oktaedrischen Löcher zu passen, können die Anionen eine offenere Struktur annehmen, z. B. eine einfache kubische Anordnung. Die größeren Kationen können dann die größeren kubischen Löcher besetzen, die durch die offeneren Abstände möglich sind.

Abbildung 13. Die Größe eines Kations und die Form des von der Verbindung besetzten Lochs stehen in direkter Beziehung zueinander.

Es gibt zwei tetraedrische Löcher für jedes Anion in einer HCP- oder CCP-Anionenanordnung. Eine Verbindung, die in einer dicht gepackten Anordnung von Anionen mit Kationen in den tetraedrischen Löchern kristallisiert, kann ein maximales Kationen:Anionen-Verhältnis von 2:1 aufweisen; alle tetraedrischen Löcher sind in diesem Verhältnis gefüllt. Beispiele hierfür sind Li2O, Na2O, Li2S und Na2S. Verbindungen mit einem Verhältnis von weniger als 2:1 können auch in einer dicht gepackten Anordnung von Anionen mit Kationen in den tetraedrischen Löchern kristallisieren, wenn die Ionengrößen passen. In diesen Verbindungen bleiben jedoch einige der tetraedrischen Löcher unbesetzt.

Das Verhältnis von oktaedrischen Löchern zu Anionen in einer HCP- oder CCP-Struktur ist 1:1. Somit können Verbindungen mit Kationen in oktaedrischen Löchern in einer dicht gepackten Anordnung von Anionen ein maximales Verhältnis von Kationen zu Anionen von 1:1 aufweisen. Bei NiO, MnS, NaCl und KH beispielsweise sind alle oktaedrischen Löcher gefüllt. Verhältnisse von weniger als 1:1 werden beobachtet, wenn einige der oktaedrischen Löcher leer bleiben.

In einer einfachen kubischen Anordnung von Anionen gibt es ein kubisches Loch, das von einem Kation für jedes Anion in der Anordnung besetzt werden kann. In CsCl und in anderen Verbindungen mit der gleichen Struktur sind alle kubischen Löcher besetzt. In SrH2, UO2, SrCl2 und CaF2 ist die Hälfte der kubischen Löcher besetzt.

Unterschiedliche Arten von ionischen Verbindungen kristallisieren oft in der gleichen Struktur, wenn die relativen Größen ihrer Ionen und ihre Stöchiometrien (die beiden Hauptmerkmale, die die Struktur bestimmen) ähnlich sind.

Einheitszellen ionischer Verbindungen

Viele ionische Verbindungen kristallisieren mit kubischen Einheitszellen, und wir werden diese Verbindungen verwenden, um die allgemeinen Merkmale ionischer Strukturen zu beschreiben.

Wenn eine ionische Verbindung aus Kationen und Anionen ähnlicher Größe in einem Verhältnis von 1:1 zusammengesetzt ist, bildet sie normalerweise eine einfache kubische Struktur. Cäsiumchlorid, CsCl, (siehe Abbildung 14) ist ein Beispiel dafür, wobei Cs+ und Cl- Radien von 174 pm bzw. 181 pm haben. Man kann sich das so vorstellen, dass die Chloridionen eine einfache kubische Einheitszelle mit einem Cäsiumion in der Mitte bilden; oder dass Cäsiumionen eine Einheitszelle mit einem Chloridion in der Mitte bilden; oder dass einfache kubische Einheitszellen, die von Cs+-Ionen gebildet werden, Einheitszellen überlappen, die von Cl–Ionen gebildet werden. Cäsiumionen und Chloridionen berühren sich entlang der Körperdiagonalen der Einheitszellen. Pro Einheitszelle sind ein Cäsium- und ein Chlorid-Ion vorhanden, so dass sich die in der Formel für Cäsiumchlorid geforderte l:l-Stöchiometrie ergibt. Man beachte, dass es keinen Gitterpunkt in der Mitte der Zelle gibt und dass CsCl keine BCC-Struktur ist, da ein Cäsium-Ion nicht mit einem Chlorid-Ion identisch ist.

Abbildung 14. Ionische Verbindungen mit gleich großen Kationen und Anionen, wie z. B. CsCl, bilden normalerweise eine einfache kubische Struktur. Sie können durch Einheitszellen beschrieben werden, bei denen entweder die Kationen an den Ecken oder die Anionen an den Ecken liegen.

Wir haben gesagt, dass die Lage der Gitterpunkte willkürlich ist. Dies wird durch eine alternative Beschreibung der CsCl-Struktur veranschaulicht, bei der sich die Gitterpunkte in den Zentren der Cäsiumionen befinden. In dieser Beschreibung befinden sich die Cäsiumionen auf den Gitterpunkten an den Ecken der Zelle, und das Chloridion befindet sich im Zentrum der Zelle. Die beiden Einheitszellen sind unterschiedlich, aber sie beschreiben identische Strukturen.

Wenn eine ionische Verbindung aus einem 1:1-Verhältnis von Kationen und Anionen besteht, die sich in ihrer Größe deutlich unterscheiden, kristallisiert sie typischerweise mit einer FCC-Einheitszelle, wie in Abbildung 15 dargestellt. Natriumchlorid, NaCl, ist ein Beispiel dafür, wobei Na+ und Cl- Radien von 102 pm bzw. 181 pm haben. Man kann sich das so vorstellen, dass die Chloridionen eine FCC-Zelle bilden, wobei sich die Natriumionen in den oktaedrischen Löchern in der Mitte der Zellränder und in der Mitte der Zelle befinden. Die Natrium- und Chloridionen berühren sich entlang der Zellränder. Die Einheitszelle enthält vier Natrium- und vier Chloridionen, so dass sich die für die Formel NaCl erforderliche Stöchiometrie von 1:1 ergibt.

Abbildung 15. Ionische Verbindungen mit Anionen, die viel größer sind als Kationen, wie z. B. NaCl, bilden normalerweise eine FCC-Struktur. Sie können durch FCC-Einheitszellen mit Kationen in den oktaedrischen Löchern beschrieben werden.

Die kubische Form von Zinksulfid, Zinkblende, kristallisiert ebenfalls in einer FCC-Einheitszelle, wie in Abbildung 16 dargestellt. Diese Struktur enthält Sulfid-Ionen auf den Gitterpunkten eines FCC-Gitters. (Die Anordnung der Sulfid-Ionen ist identisch mit der Anordnung der Chlorid-Ionen in Natriumchlorid.) Der Radius eines Zink-Ions beträgt nur etwa 40 % des Radius eines Sulfid-Ions, so dass sich diese kleinen Zn2+-Ionen in alternierenden tetraedrischen Löchern befinden, d. h. in einer Hälfte der tetraedrischen Löcher. In der Einheitszelle befinden sich vier Zink- und vier Sulfid-Ionen, was die empirische Formel ZnS ergibt.

Abbildung 16. ZnS, Zinksulfid (oder Zinkblende) bildet eine FCC-Einheitszelle mit Sulfidionen an den Gitterpunkten und viel kleineren Zinkionen, die die Hälfte der tetraedrischen Löcher in der Struktur besetzen.

Eine Kalziumfluorid-Einheitszelle, wie in Abbildung 17 dargestellt, ist ebenfalls eine FCC-Einheitszelle, aber in diesem Fall befinden sich die Kationen an den Gitterpunkten; entsprechende Kalziumionen befinden sich an den Gitterpunkten eines FCC-Gitters. Alle tetraedrischen Plätze in der FCC-Anordnung der Calciumionen werden von Fluoridionen besetzt. In einer Einheitszelle befinden sich vier Calciumionen und acht Fluoridionen, was ein Calcium:Fluor-Verhältnis von l:2 ergibt, wie es die chemische Formel CaF2 verlangt. Bei genauer Betrachtung von Abbildung 17 erkennt man eine einfache kubische Anordnung von Fluoridionen mit Calciumionen in einer Hälfte der kubischen Löcher. Die Struktur kann nicht durch ein Raumgitter mit Punkten auf den Fluoridionen beschrieben werden, da die Fluoridionen nicht alle die gleiche Umgebung haben. Die Ausrichtung der vier Kalziumionen zu den Fluoridionen ist unterschiedlich.

Abbildung 17. Calciumfluorid, CaF2, bildet eine FCC-Einheitszelle mit Calciumionen (grün) an den Gitterpunkten und Fluoridionen (rot), die alle tetraedrischen Plätze dazwischen besetzen.

Berechnung von Ionenradien

Wenn wir die Kantenlänge einer Einheitszelle einer Ionenverbindung und die Position der Ionen in der Zelle kennen, können wir die Ionenradien für die Ionen in der Verbindung berechnen, wenn wir Annahmen über die einzelnen Ionenformen und -kontakte machen.

Beispiel 5: Berechnung von Ionenradien

Die Kantenlänge der Einheitszelle von LiCl (NaCl-ähnliche Struktur, FCC) beträgt 0.514 nm oder 5,14 Å. Unter der Annahme, dass das Lithium-Ion klein genug ist, so dass die Chlorid-Ionen in Kontakt sind, wie in Abbildung 15, berechnen Sie den Ionenradius für das Chlorid-Ion.

Hinweis: Die Längeneinheit Angström, Å, wird oft zur Darstellung von Dimensionen auf atomarer Ebene verwendet und entspricht 10-10 m.

Zeige die Lösung

Auf der Fläche einer LiCl-Einheitszelle berühren sich die Chloridionen über die Diagonale der Fläche:

Zieht man ein rechtwinkliges Dreieck auf die Fläche der Einheitszelle, so sieht man, dass die Länge der Diagonale vier Chloridradien entspricht (ein Radius von jedem Eckchlorid und ein Durchmesser – der zwei Radien entspricht – vom Chloridion in der Mitte der Fläche), also d = 4r. Aus dem Satz des Pythagoras ergibt sich:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}

das ergibt:

\links(0.514\text{ nm}\rechts)^{2}+\links(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) für einen Cl-Radius

Kontrollieren Sie Ihr Wissen

Die Kantenlänge der Einheitszelle von KCl (NaCl-ähnliche Struktur, FCC) beträgt 6,28 Å. Berechnen Sie unter der Annahme eines Anionen-Kationen-Kontakts entlang der Zellkante den Radius des Kalium-Ions. Der Radius des Chlorid-Ions beträgt 1,82 Å.

Lösung anzeigen

Der Radius des Kalium-Ions beträgt 1,33 Å.

Es ist wichtig zu wissen, dass die aus den Kantenlängen der Einheitszellen berechneten Werte für die Ionenradien von zahlreichen Annahmen abhängen, wie z.B. einer perfekten Kugelform der Ionen, die bestenfalls Näherungswerte sind. Daher sind solche berechneten Werte selbst Näherungswerte, und Vergleiche können nicht zu weit getrieben werden. Dennoch hat sich diese Methode als nützlich erwiesen, um Ionenradien aus experimentellen Messungen wie röntgenkristallographischen Bestimmungen zu berechnen.

Röntgenkristallographie

Die Größe der Einheitszelle und die Anordnung der Atome in einem Kristall können durch Messungen der Beugung von Röntgenstrahlen durch den Kristall bestimmt werden, was als Röntgenkristallographie bezeichnet wird. Unter Beugung versteht man die Änderung der Ausbreitungsrichtung einer elektromagnetischen Welle, wenn sie auf ein physikalisches Hindernis trifft, dessen Abmessungen mit denen der Wellenlänge des Lichts vergleichbar sind. Röntgenstrahlen sind elektromagnetische Strahlung mit Wellenlängen, die etwa so lang sind wie der Abstand zwischen benachbarten Atomen in Kristallen (in der Größenordnung von einigen Å).

Wenn ein Strahl monochromatischer Röntgenstrahlen auf einen Kristall trifft, werden seine Strahlen von den Atomen im Kristall in alle Richtungen gestreut. Wenn gestreute Wellen, die sich in die gleiche Richtung bewegen, aufeinander treffen, kommt es zur Interferenz, einem Prozess, bei dem sich die Wellen kombinieren, um entweder eine Zunahme oder eine Abnahme der Amplitude (Intensität) zu erzielen, je nachdem, wie weit die Maxima der kombinierenden Wellen voneinander entfernt sind (siehe Abbildung 18).

Abbildung 18. Lichtwellen, die denselben Raum einnehmen, interferieren und kombinieren sich zu Wellen größerer (a) oder geringerer (b) Intensität, je nach dem Abstand ihrer Maxima und Minima.

Wenn Röntgenstrahlen einer bestimmten Wellenlänge λ von Atomen in benachbarten Kristallebenen gestreut werden, die durch einen Abstand d voneinander getrennt sind, können sie konstruktive Interferenz erfahren, wenn der Unterschied zwischen den von den beiden Wellen vor ihrer Kombination zurückgelegten Strecken ein ganzzahliger Faktor n der Wellenlänge ist. Diese Bedingung ist erfüllt, wenn der Winkel des gebeugten Strahls, θ, mit der Wellenlänge und dem Abstand zwischen den Atomen durch die Gleichung in Beziehung steht:

n{\lambda }=2d\text{sin}\theta

Diese Beziehung ist als Bragg-Gleichung bekannt, zu Ehren von W. H. Bragg, dem englischen Physiker, der dieses Phänomen als erster erklärte. Abbildung 19 zeigt zwei Beispiele für gebeugte Wellen an denselben beiden Kristallebenen. Die Abbildung auf der linken Seite zeigt Wellen, die unter dem Bragg-Winkel gebeugt werden, was zu konstruktiver Interferenz führt, während die Abbildung auf der rechten Seite die Beugung unter einem anderen Winkel zeigt, der die Bragg-Bedingung nicht erfüllt, was zu destruktiver Interferenz führt.

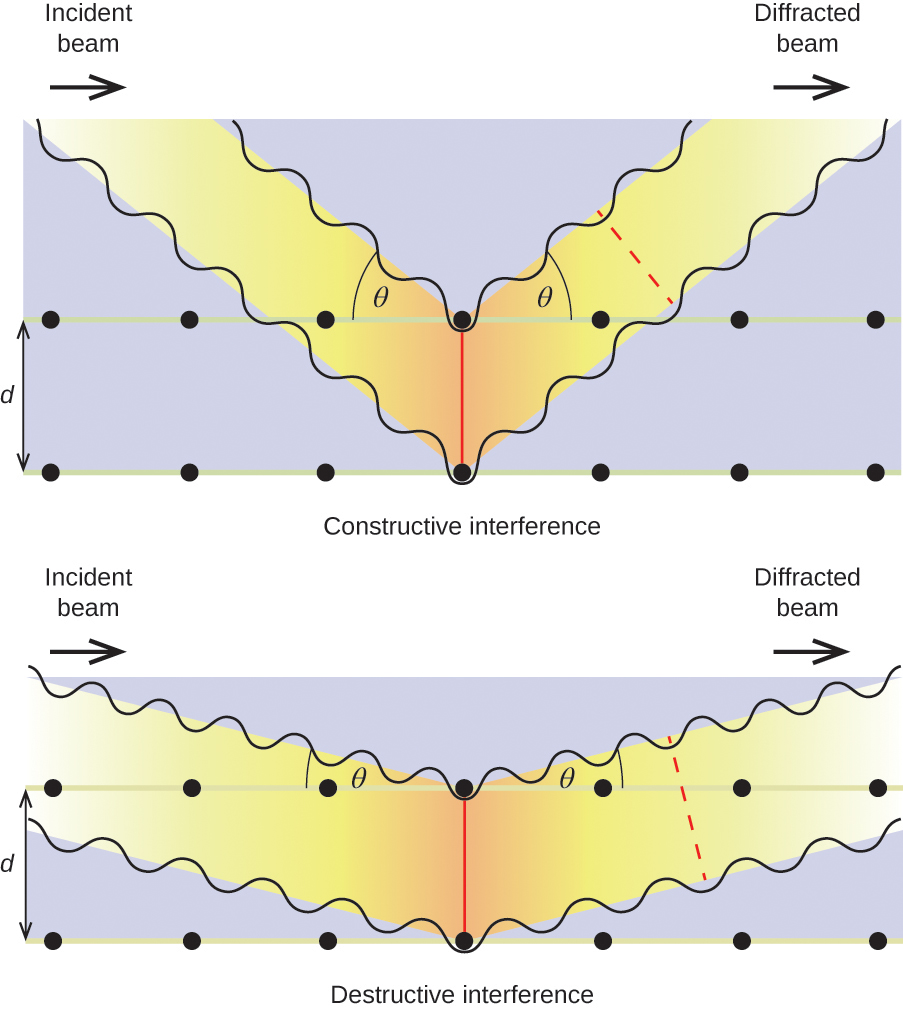
Abbildung 19. Die Beugung von Röntgenstrahlen, die von den Atomen in einem Kristall gestreut werden, ermöglicht die Bestimmung des Abstands zwischen den Atomen. Das obere Bild zeigt die konstruktive Interferenz zwischen zwei gestreuten Wellen und eine daraus resultierende gebeugte Welle mit hoher Intensität. Das untere Bild zeigt die destruktive Interferenz und eine gebeugte Welle mit geringer Intensität.

Mit einem Röntgendiffraktometer, wie dem in Abbildung 20 dargestellten, können die Winkel gemessen werden, unter denen Röntgenstrahlen bei der Wechselwirkung mit einem Kristall wie oben beschrieben gebeugt werden. Anhand solcher Messungen kann die Bragg-Gleichung zur Berechnung der Abstände zwischen den Atomen verwendet werden, wie im folgenden Übungsbeispiel gezeigt wird.

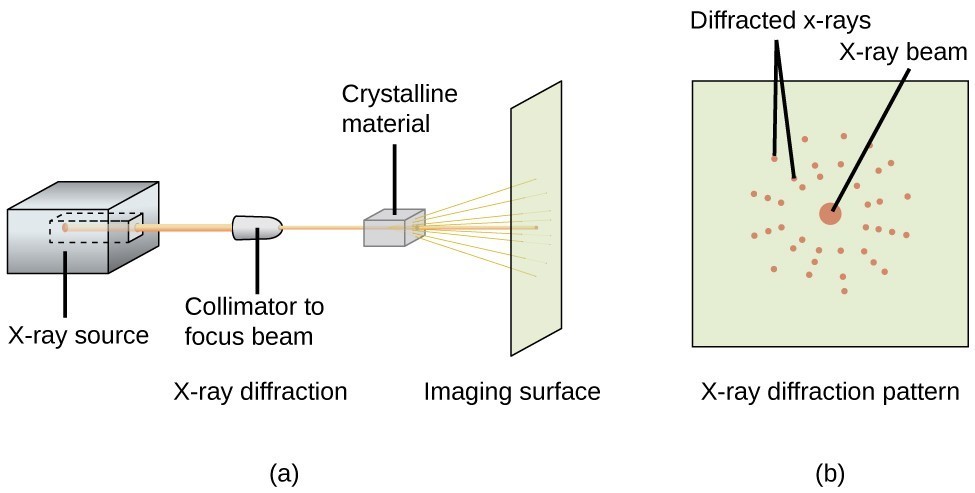
Abbildung 20. In einem Diffraktometer (a) trifft ein Röntgenstrahl auf ein kristallines Material und erzeugt ein Röntgenbeugungsmuster (b), das analysiert werden kann, um die Kristallstruktur zu bestimmen.

Das Transkript zu „Celebrating Crystallography – An animated adventure“ können Sie hier ansehen (öffnet in neuem Fenster).

Porträt einer Chemikerin: Röntgenkristallografin Rosalind Franklin

Abbildung 21. Diese Abbildung zeigt ein Röntgenbeugungsbild, das dem ähnelt, das Franklin bei ihrer Forschung gefunden hat. (credit: National Institutes of Health)

Die Entdeckung der Struktur der DNA im Jahr 1953 durch Francis Crick und James Watson ist eine der größten Errungenschaften in der Geschichte der Wissenschaft. Sie erhielten 1962 den Nobelpreis für Physiologie oder Medizin, ebenso wie Maurice Wilkins, der den experimentellen Nachweis der DNA-Struktur erbrachte. Die britische Chemikerin Rosalind Franklin leistete mit ihrer Arbeit zur Messung von Röntgenbeugungsbildern der DNA einen unschätzbaren Beitrag zu dieser monumentalen Leistung. Zu Beginn ihrer Karriere erwies sich Franklins Forschung über die Struktur von Kohle als hilfreich für die britischen Kriegsanstrengungen. Nachdem sie Anfang der 1950er Jahre ihren Schwerpunkt auf biologische Systeme verlegt hatte, entdeckten Franklin und ihr Doktorand Raymond Gosling, dass die DNA aus zwei Formen besteht: einer langen, dünnen Faser, die sich im nassen Zustand bildet (Typ „B“), und einer kurzen, breiten Faser, die sich beim Trocknen bildet (Typ „A“). Ihre Röntgenbeugungsbilder der DNA (Abbildung 21) lieferten die entscheidenden Informationen, die es Watson und Crick ermöglichten, zu bestätigen, dass die DNA eine Doppelhelix bildet, und Details ihrer Größe und Struktur zu bestimmen.

Franklin führte auch bahnbrechende Forschungen über Viren und die RNA, die ihre genetischen Informationen enthält, durch und entdeckte dabei neue Informationen, die den Wissensstand auf diesem Gebiet radikal veränderten. Nachdem sie an Eierstockkrebs erkrankt war, arbeitete Franklin bis zu ihrem Tod 1958 im Alter von 37 Jahren weiter. Zu den vielen posthumen Anerkennungen ihrer Arbeit gehört, dass die Chicago Medical School der Finch University of Health Sciences 2004 ihren Namen in Rosalind Franklin University of Medicine and Science änderte und ein Bild ihrer berühmten Röntgenbeugungsaufnahme der DNA als offizielles Universitätslogo übernahm.

Glossar

Körperzentrierter kubischer (BCC) Festkörper: kristalline Struktur, die eine kubische Einheitszelle mit Gitterpunkten an den Ecken und in der Mitte der Zelle besitzt

Körperzentrierte kubische Einheitszelle: einfachste sich wiederholende Einheit eines kubisch-raumzentrierten Kristalls; es handelt sich um einen Würfel mit Gitterpunkten an jeder Ecke und im Zentrum des Würfels

Bragg-Gleichung: Gleichung, die sich auf die Winkel bezieht, unter denen Röntgenstrahlen von den Atomen innerhalb eines Kristalls gebeugt werden

Koordinationszahl: Anzahl der Atome, die einem bestimmten Atom in einem Kristall oder dem zentralen Metallatom in einem Komplex am nächsten liegen

cubic closest packing (CCP): Kristallstruktur, bei der Ebenen dicht gepackter Atome oder Ionen als eine Reihe von drei abwechselnden Schichten mit unterschiedlicher relativer Ausrichtung (ABC) gestapelt sind

Beugung: Umlenkung elektromagnetischer Strahlung, die auftritt, wenn sie auf eine physikalische Barriere geeigneter Abmessungen trifft

flächenzentrierter kubischer (FCC) Festkörper: kristalline Struktur, die aus einer kubischen Einheitszelle mit Gitterpunkten an den Ecken und in der Mitte jeder Fläche besteht

flächenzentrierte kubische Einheitszelle: einfachste sich wiederholende Einheit eines flächenzentrierten kubischen Kristalls; es ist ein Würfel, der Gitterpunkte an jeder Ecke und im Zentrum jeder Fläche enthält

hexagonal engste Packung (HCP): kristalline Struktur, in der dicht gepackte Schichten von Atomen oder Ionen als eine Reihe von zwei abwechselnden Schichten mit unterschiedlichen relativen Orientierungen gestapelt sind (AB)

Loch: (auch, Zwischenraum) Raum zwischen Atomen innerhalb eines Kristalls

isomorph: die gleiche kristalline Struktur besitzend

oktaedrisches Loch: offener Raum in einem Kristall im Zentrum von sechs Teilchen, die sich an den Ecken eines Oktaeders befinden

einfache kubische Einheitszelle: (auch primitive kubische Einheitszelle) Einheitszelle in der einfachen kubischen Struktur

einfache kubische Struktur: kristalline Struktur mit einer kubischen Einheitszelle mit Gitterpunkten nur an den Ecken

Raumgitter: alle Punkte innerhalb eines Kristalls, die identische Umgebungen haben

tetraedrisches Loch: tetraedrischer Raum, der von vier Atomen oder Ionen in einem Kristall gebildet wird

Einheitszelle: kleinster Teil eines Raumgitters, der sich in drei Dimensionen wiederholt, um das gesamte Gitter zu bilden

Röntgenkristallographie: experimentelle Technik zur Bestimmung von Abständen zwischen Atomen in einem Kristall durch Messung der Winkel, unter denen Röntgenstrahlen beim Durchgang durch den Kristall gebeugt werden