Wozu sind Zeichentafeln gut?

An dieser Stelle ist eine gute Frage: Wozu soll man etwas über Zeichentafeln lernen? Die einfache Antwort ist, dass die Symmetrie und die zugehörige Zeichentabelle eines Moleküls verwendet werden kann, um viele Aspekte der chemisch bedeutsamen Spektroskopie sowie der Bindungen zu interpretieren und vorherzusagen. Wir werden dies im Folgenden anhand der Schwingungsmoden eines Moleküls veranschaulichen.

Im Labor können wir mit Hilfe der Infrarot- (IR) und Raman-Spektroskopie nützliche experimentelle Daten sammeln. Diese Daten können mit der Anzahl der aktiven IR- und/oder Raman-Banden verglichen werden, die durch die Anwendung der Gruppentheorie und der korrekten Zeichentabelle vorhergesagt werden. Die Mathematik (Gruppentheorie und Matrixalgebra), die hinter dieser Behandlung steht, dient als solide theoretische Grundlage. Die unten beschriebenen Manipulationen funktionieren, weil alle Symmetrieoperationen eines Moleküls eine mathematische Gruppe bilden und den Regeln der Gruppe gehorchen. Wie bereits erwähnt, müssen wir diesen Bereich der Mathematik nicht beherrschen, um die Zeichentabellen sinnvoll nutzen zu können.

Freiheitsgrade und Schwingungen in Molekülen

Hier werden wir zunächst die Freiheitsgrade für ein einfaches Molekül (Wasser) diskutieren. Wir werden sehr schnell sehen, warum es sehr vorteilhaft ist, Symmetrie zu verwenden, wenn wir größere Moleküle untersuchen.

Für ein Molekül mit „N“ Atomen gibt es 3N Freiheitsgrade (wir leben in einer dreidimensionalen Welt mit x, y, z Koordinaten). Bei einem nichtlinearen Molekül können 3 Freiheitsgrade auf Translationen – Bewegung eines Körpers als Ganzes (Tx, Ty, Tz) und 3 auf Rotationen (Rx, Ry, Rz) bezogen werden. Die übrigen Bewegungen der Atome sind Verschiebungen der Atome aus ihrer mittleren Position – der Schwerpunkt ändert sich nicht. Diese Grundschwingungen werden als „Normalmoden“ bezeichnet. Ein nichtlineares Molekül hat also 3N-6 Normalmoden. Für Wasser beträgt die Anzahl der Normalmoden 3 (3 x 3 – 6 = 3). Für lineare Moleküle gibt es 3N-5 Normalmoden.

Für Wasser, das natürlich intensiv untersucht wurde, wissen wir, dass die 3 Schwingungen wie folgt sind.

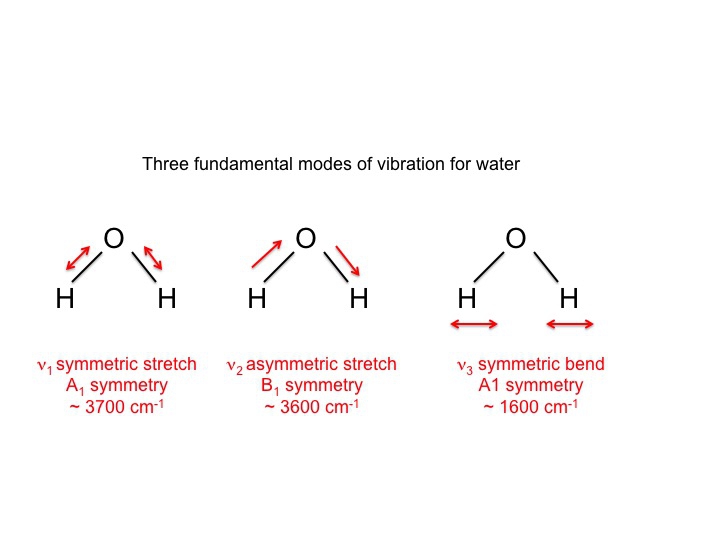
Die Symbole, die zur Beschreibung dieser Moden (A1, B1) verwendet werden, sind die gleichen Mulliken-Symbole, die wir in unserer Diskussion über Zeichentabellen kennengelernt haben. Mit anderen Worten, die Schwingungen, die molekulare Eigenschaften sind, können durch Symmetriearten oder irreduzible Darstellungen beschrieben werden. Ein Großteil der Literatur zur Schwingungsspektroskopie verwendet diese Symbole als Kurzform für die Übermittlung von Informationen.

Es sollte ziemlich offensichtlich sein, dass die Anzahl der Schwingungen selbst bei einer geringen Zunahme der Anzahl der Atome im Molekül rasch zunimmt. Die Bestimmung der Arten von Schwingungen durch Inspektion (wie bei Wasser) wird nun sehr viel schwieriger. Betrachten wir zum Beispiel die folgenden Verbindungen:

H2O 3 Atome 3 Schwingungen

PH3 4 Atome 6 Schwingungen

CO22- 4 Atome 6 Schwingungen

XeF4 5 Atome 9 Schwingungen

B2H6 8 Atome 18 Schwingungen

Für Diboran (B2H6), das eine D2h-Symmetrie aufweist, wäre es eine gewaltige Aufgabe, die Natur und die Symmetrieart aller 18 Schwingungen durch Inspektion zu bestimmen. Mit der Zeichentabelle für D2h und der Kenntnis der Symmetrieeigenschaften ist es jedoch ein Leichtes, die Symmetriearten aller Schwingungen zu bestimmen.

Für den Fall von Wasser könnten wir die Zeichentabelle (C2v) mit den drei Schwingungen (ν1, v2, v3) in der Spalte der Moleküleigenschaften wie unten gezeigt darstellen. (ν = griechisches Symbol „nu“)

Allerdings ist dieser Ansatz im Allgemeinen unpraktisch. Nehmen wir zum Beispiel Pyridin (C5H5N). Die Punktgruppe ist ebenfalls C2v, aber das Molekül hat 11 Atome. Die Anzahl der Grundschwingungsformen beträgt 27 ( 3 x 11 – 6 = 27).

In diesem Fall müssten wir eine C2v-Zeichentabelle aufstellen, die die Symmetrien aller 27 Schwingungen zeigt. Aus diesem Grund werden Schwingungen normalerweise nicht in Zeichentabellen aufgenommen. Stattdessen ist es Aufgabe des Benutzers (also von Ihnen), die Anzahl und die Art der Schwingungen (definiert durch ihre Symmetriearten) für alle vorkommenden Moleküle zu bestimmen. Wie wir dies tun, wird im Folgenden beschrieben.

Reduzierbare Darstellungen

Wie bereits erwähnt, ist eine der wichtigen Eigenschaften von Zeichentabellen, dass die Symmetrieoperationen Mitglieder einer mathematischen Gruppe sind und wichtige Beziehungen zwischen ihnen bestehen. Im Allgemeinen kann dasselbe über die Symmetriearten oder irreduziblen Darstellungen der molekularen Eigenschaften gesagt werden. Die Produkte aus der Kombination der Zeichen irreduzibler Darstellungen entweder durch Multiplikation oder Addition/Subtraktion gehorchen ebenfalls den Regeln der Gruppe. Die neuen Darstellungen sind nicht mehr die einfachsten und werden als „reduzierbare Darstellungen“ bezeichnet, weil sie auf ihre Bestandteile „reduziert“ werden können.

Für Wasser zum Beispiel können die Symmetrien der Translationen (Tx, Ty, Tz) direkt aus der C2v-Zeichentabelle entnommen werden. Sie lauten A1, B1 und B2. Wir können alle drei dieser Freiheitsgrade durch eine Darstellung ΓT darstellen und den folgenden Ausdruck schreiben. (Γ = griechischer Großbuchstabe „gamma“).

ΓT = A1 + B1 + B2

Wir wissen, dass A1, B1 und B2 lediglich die Kurzbezeichnungen für die Symmetriearten (nicht reduzierbare Darstellungen) sind. Wir können daher die Zeichen von ΓT einfach aufschreiben, indem wir die einzelnen Zeichen für A1, B1 und B2 aus der C2v-Zeichentabelle addieren.

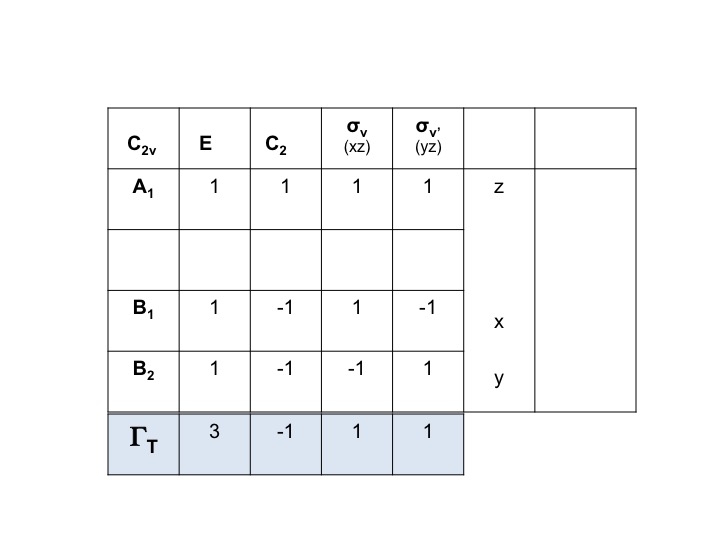
Damit ist ΓT = 3 -1 1 1.

Dies ist eine gültige reduzierbare Darstellung und ein Mitglied der C2v-Gruppe.

Auf ähnliche Weise können wir die reduzierbare Darstellung für alle drei Drehungen und alle Schwingungen aufschreiben.

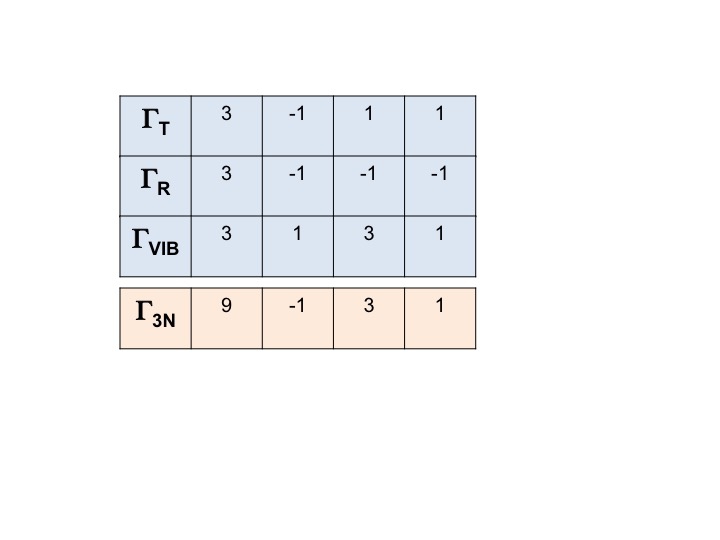
Die Darstellung für ALLE Freiheitsgrade des Moleküls (3N) kann geschrieben werden als

Γ3N = ΓT + ΓR + ΓVIB

und die reduzierbare Darstellung dafür erhält man durch einfache Summierung der Zeichen für ΓT, ΓR und ΓVIB.

Γ3N = 9 -1 3 1

Merken Sie sich das – es wird später auftauchen!

Obwohl die Menge der Zeichen 9 -1 3 1 ein gültiges Mitglied der C2v-Gruppe ist, ist sie bei der Diskussion molekularer Eigenschaften nicht besonders nützlich. Was wir wirklich brauchen, ist die Sprache der Kurzsymmetriearten (Mulliken-Symbole, A1, B1 usw.). Mit anderen Worten, wir wollen Γ3N in Form von A1, B1 usw. ausdrücken. Anhand der oben genannten Informationen lässt sich leicht zeigen, dass:

Γ3N = 3A1 +A2 + 3B1 +2B2

Die gute Nachricht ist, dass wir diese Aufgabe für andere, komplexere Moleküle nicht durch Einsichtnahme erledigen müssen, denn:

1. Wir können Γ3N leicht als reduzierbare Darstellung für ein Molekül erzeugen (wenn wir seine Punktgruppensymmetrie kennen).

2. Wir können die reduzierbare Γ3N-Darstellung leicht in die Summe seiner Symmetriearten (Mulliken-Symbole) umwandeln, indem wir eine „einfache“ Formel, die sogenannte Reduktionsformel, verwenden.

Allgemeine Methode zur Gewinnung von Γ3N

Schritt 1

Nehmen Sie die Zeichentabelle für das Molekül und fügen Sie eine Zeile am unteren Ende hinzu. In dieser Zeile erzeugen Sie die reduzierbare Darstellung für ΓT (oder Γxyz), wie wir es oben getan haben, indem Sie einfach die Zeichen für jede Operation hinzufügen, die den molekularen Eigenschaften für x, y und z entsprechen. Für C2v haben wir bereits gezeigt, dass dies die Zeichen sind, die A1, B1 und B2 entsprechen.

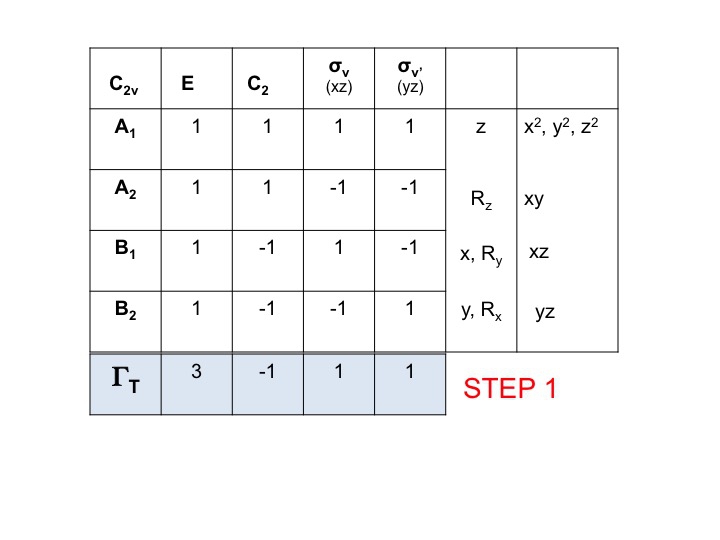
Schritt 2

Fügen Sie eine weitere Zeile unter ΓT ein und notieren Sie die Anzahl der Atome, die ihre Lage während jeder Symmetrieoperation NICHT verändern. Hier wird deutlich, wie nützlich ein echter Molekülmodellsatz ist. Dazu müssen Sie auch wissen, wo sich die Symmetrieelemente befinden und wie die Symmetrieoperationen das Molekül beeinflussen. Natürlich wissen Sie bereits, wie man das macht, weil Sie die Schönflies-Notation studiert haben und wissen, wie man die Punktgruppe eines Moleküls zuordnet. In der Zeichentabelle sind auch alle Symmetrieoperationen nach Klassen in der obersten Zeile aufgelistet.

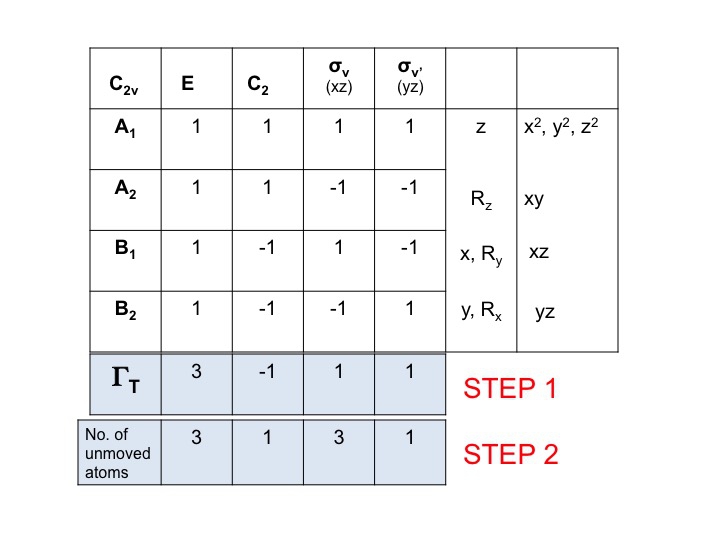
So gibt es für Wasser (3 Atome) unter E 3 unbewegte Atome, aber für C2 bewegen sich beide H-Atome, aber da das O-Atom auf der C2-Achse sitzt, ändert es seine Position nicht, und so notieren wir 1 unter der C2-Spalte. Die in Schritt 2 erzeugte neue Zahlenmenge (3 1 3 1) ist ebenfalls eine reduzierbare Darstellung in C2v und gehorcht den Regeln der Gruppe.

Schritt 3

In diesem Schritt multiplizieren wir einfach die Zeichen, die in Schritt 1 und 2 erzeugt wurden. Das Ergebnis (dritte Zeile) ist die reduzierbare Darstellung für Γ3N (oder ΓTOT). So einfach ist das.

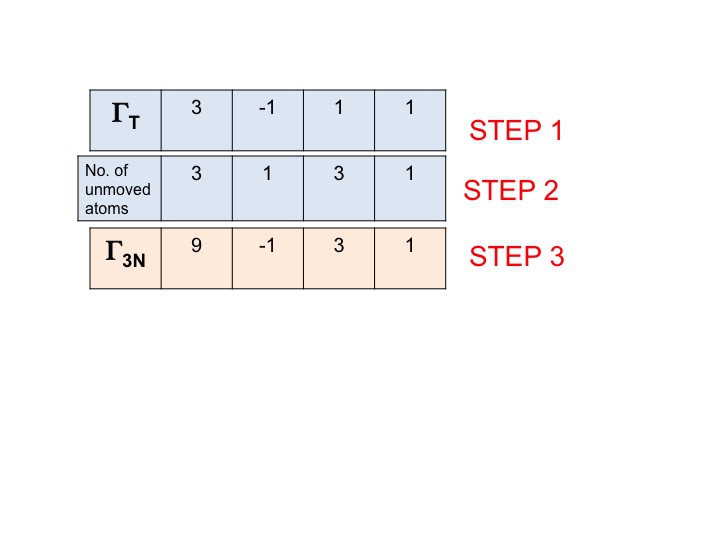
Sie werden feststellen, dass die neue reduzierbare Darstellung (9 -1 1 3) identisch ist mit der Darstellung für Γ3N, die wir zuvor durch Überprüfung erhalten haben.

Reduzierung der reduzierbaren Darstellung

Um eine beliebige reduzierbare Darstellung in die Summe ihrer irreduziblen Darstellungen (Symmetriearten oder Mulliken-Symbole) umzuwandeln, verwenden wir eine Reduktionsformel:

Diese Informationen können Sie leicht in der Zeichentabelle finden:

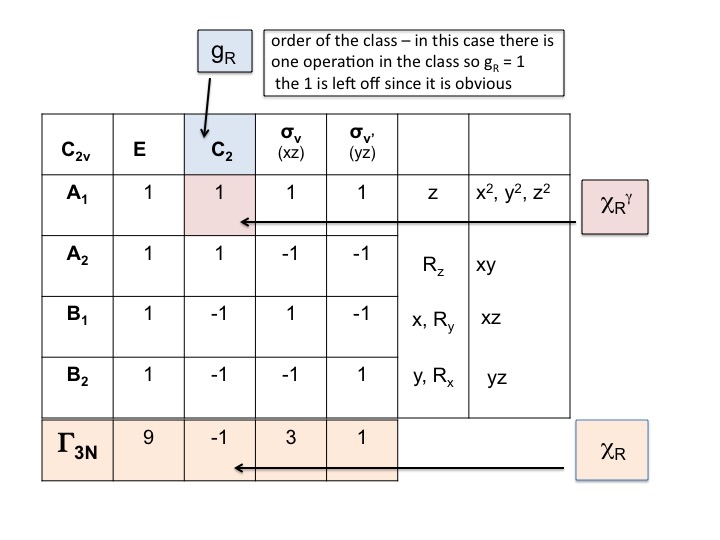
Zurück zu unserem Beispiel für Wasser: Punktgruppe C2v, Ordnung (g) = 4

Die reduzierbare Darstellung für Γ3N = 9 -1 3 1

Die Anzahl, wie oft A1 in dieser Darstellung vorkommt, ist also

aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3

also enthält Γ3N 3 A1-Symmetriearten. Die Anzahl der anderen Symmetriearten wird wie folgt berechnet:

aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 eine A2 vorhanden

aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 B1 vorhanden

aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1} = 2 2 B2 vorhanden

Wir können nun schreiben Γ3N = 3A1 + A2 + 3B1 + 2B2 (genau das, was wir durch „Inspektion“ oben erhalten haben. Wir können nun die Symmetriearten für die Translationen und Rotationen subtrahieren und erhalten so die Anzahl und Symmetriearten der Grundschwingungsformen. ΓT und ΓR können direkt aus der Zeichentabelle entnommen werden.

Γ3N = 3A1 + A2 + 3B1 + 2B2

ΓT = A1 + B1 + B2

ΓR = A2 + B1 + B2

ΓVIB = Γ3N – ΓT – ΓR = 2A1 +B1

Die drei Normalschwingungsformen für Wasser haben also die Symmetrien A1, A1 und B1.

Wir haben nun eine allgemeine Methode, um alle Grundschwingungsformen eines Moleküls zu bestimmen und diese in der Kurzsprache der Mulliken-Symbole auszudrücken. Dies ist eine der Aufgaben, die Sie in Prüfung 1 bearbeiten müssen. Der beste Weg, um mit dieser Methode vertraut zu werden, ist, so viele mögliche Beispiele wie möglich zu üben!

Weiter: Auswahlregeln