Mindre…
En pythagoræisk trippel er en trippel af positive hele tal 
, 
og 
, således at der findes en retvinklet trekant med benene 
og hypotenusen 
. Ved hjælp af Pythagoras sætning svarer dette til at finde positive hele tal 
, 
og 
, der opfylder
 |
(1)
|
Den mindste og mest kendte pythagoræiske tripel er 
. Den retvinklede trekant med disse sidelængder kaldes undertiden for 3, 4, 5 trekanten.
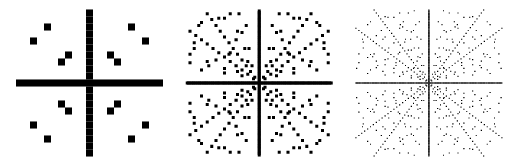
Plots af punkter i 
-planet, således at 
er en pythagoræisk trippel, er vist ovenfor for successivt større grænser. Disse plotter omfatter negative værdier af 
og 
og er derfor symmetriske omkring både x- og y-aksen.
På samme måde er plotter af punkter i 
-planet, således at 
er en pythagoræisk tripel, vist ovenfor for successivt større grænser.
Det er almindeligt kun at betragte primitive pythagoræiske tripler (også kaldet “reducerede “tripler), hvor 
og 
er relativt primtal, da andre løsninger kan genereres trivielt fra de primitive. De primitive tripler er illustreret ovenfor, og det kan straks ses, at de radiale linjer, der svarer til imprimitive tripler i det oprindelige plot, er fraværende i denne figur. For primitive løsninger skal en af 
eller 
være lige, og den anden ulige (Shanks 1993, s. 141), med 
altid ulige.
Dertil kommer, at den ene side af hver pythagoræisk tripel er delbar med 3, en anden med 4 og en anden med 5. Den ene side kan have to af disse divisorer, som i (8, 15, 17), (7, 24, 25) og (20, 21, 29), eller endda alle tre, som i (11, 60, 61).
Givet en primitiv tripel 
, fås tre nye primitive triplaer fra
 |
 |
 |
(2)
|
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
hvor
 |
 |
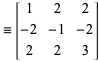(5)
|
 |
 |
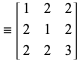(6)
|
 |
 |
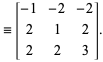(7)
|
Hall (1970) og Roberts (1977) beviser, at 
er en primitiv pythagoræisk tripel, hvis
 |
(8)
|
hvor 
er et endeligt produkt af matricerne 
, 
, 
. Det følger derfor, at enhver primitiv pythagoræisk trippel må være et medlem af den uendelige matrix
 |
(9)
|
Pythagoras og babylonierne gav en formel til generering af (ikke nødvendigvis primitive) tripler som
 |
(10)
|
for 
, som genererer et sæt af distinkte tripler, der hverken indeholder alle primitive eller alle imprimitive tripler (og hvor der i det særlige tilfælde 
, 
).
De tidlige grækere gav
 |
(11)
|
hvor 
og 
er relativt primtal og af modsat paritet (Shanks 1993, p. 141), hvilket genererer et sæt af distinkte tripler, der netop indeholder de primitive tripler (efter passende sortering af 
og 
).
Lad 
være et Fibonacci-tal. Så
 |
(12)
|
genererer tydelige pythagoræiske tripler (Dujella 1995), om end ikke udtømmende for hverken primitive eller imprimitive tripler. Mere generelt starter man med positive hele tal 
, 
og konstruerer den Fibonacci-lignende sekvens 
med termerne 
, 
, 
, 
, 
, … genererer forskellige pythagoræiske tripler
 |
(13)
|
(Horadam 1961), hvor
 |
(24)
|
(Beiler 1966, p. 116). Bemærk, at 
hvis 
er primtal eller to gange et primtal. De første tal for 
, 2, … er 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 1, 4, 1, 1, … (OEIS A046079).
For at finde antallet af måder 
, hvorpå et tal 
kan være hypotenuse i en primitiv retvinklet trekant, skal du skrive dets faktorisering som
 |
(25)
|
hvor de 
s er af formen 
og de 
s er af formen 
. Antallet af mulige primitive retvinklede trekanter er så
 |
(26)
|
For eksempel, 
da
 |
 |
 |
(27)
|
 |
 |
 |
(28)
|
Værdierne af 
for 
, 2, … er 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, … (OEIS A024362). De første få primtal af formen 
er 5, 13, 17, 29, 29, 37, 41, 41, 53, 61, 61, 73, 89, 97, 97, 101, 109, 113, 137, … (OEIS A002144), så de mindste sidelængder, som er hypotenuserne i 1, 2, 4, 8, 16, … primitive retvinklede trekanter, er 5, 65, 1105, 32045, 1185665, 48612265, … (OEIS A006278).
Antallet af mulige primitive eller ikke-primitive retvinklede trekanter med 
som hypotenuse er
 |
 |
 |
(29)
|
 |
 |
 |
(30)
|
(rettelse af stavefejl i Beiler 1966, p. 117, hvor der står, at denne formel kun giver antallet af ikke-primitive løsninger), hvor 
er summen af kvadraternes funktion. For eksempel er der fire forskellige hele trekanter med hypotenuse 65, da
 |
(31)
|
De første tal for 
, 2, … er 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, … (OEIS A046080). De mindste hypotenuser med 
forskellige tripler er 1, 5, 25, 125, 65, 3125, … (OEIS A006339). Følgende tabel angiver de hypotenuser, for hvilke der findes præcis 
forskellige retvinklede hele trekanter for 
, 1, …, 5.
 |
OEIS | hypotenuser, for hvilke der findes  forskellige hele trekanter |
| 0 | A004144 | 1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, … |
| 1 | A084645 | 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, … |
| 2 | A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, … |
| A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, … | |
| 3 | A084647 | 125, 250, 375, 500, 750, 875, 1000, 1125, 1375, … |
| 4 | A084648 | 65, 85, 130, 145, 170, 170, 185, 195, 195, 205, 221, 255, … |
| 5 | A084649 | 3125, 6250, 9375, 12500, 18750, 21875, 25000, … |
Derfor er det samlede antal måder, hvorpå 
kan være enten et ben eller en hypotenuse i en retvinklet trekant givet ved
 |
(32)
|
Værdierne for 
, 2, … er 0, 0, 0, 1, 1, 1, 2, 2, 1, 1, 1, 2, 2, 2, 2, 2, 1, 4, 2, 1, 5, 3, … (OEIS A046081). De mindste tal 
, som kan være siderne af 
almindelige retvinklede trekanter for 
, 2, … er 3, 5, 16, 12, 15, 125, 24, 40, … (OEIS A006593; Beiler 1966, s. 114).
Der findes 50 pythagoræiske tripler med hypotenuse mindre end 100, hvoraf de første par, sorteret efter stigende 
, er (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084 og A009000).
Af disse er kun 16 primitive tripletter med hypotenuse mindre end 100: (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89), og (65, 72, 97) (OEIS A046086, A046087, og A020882).
Lad antallet af tripler med hypotenusen 
betegnes 
, antallet af tripler med hypotenusen 
betegnes 
, og antallet af primitive tripler mindre end 
betegnes 
. Derefter opsummeres værdierne for potenser af 10 i følgende tabel:
 |
OEIS |  ,  , … |
 |
A101929 | 1, 50, 878, 12467, … |
 |
A101930 | 2, 52, 881, 12471, … |
|
A101930 | 2, 52, 881, 12471, … |
| .. | ||
 |
A101931 | 1, 16, 158, 1593, … |
Lehmer (1900) beviste, at antallet af primitive løsninger med hypotenuse mindre end 
opfylder
 |
(33)
|
(OEIS A086201).
Inradiierne af de første få primitive pythagoræiske trekanter ordnet efter stigende 
er givet ved 1, 2, 3, 3, 3, 6, 6, 5, 4, 10, 5, … (OEIS A014498).
Der findes en generel metode til at opnå tripletter af pythagoræiske trekanter med lige store arealer. Tag de tre sæt generatorer som
 |
 |
 |
(34)
|
 |
 |
 |
(35)
|
 |
 |
 |
(36)
|
 |
 |
 |
(37)
|
 |
 |
 |
(38)
|
 |
 |
 |
(39)
|
Så er den retvinklede trekant genereret af hver tripel (
) har fælles areal
 |
(40)
|
(Beiler 1966, pp. 126-127). Det eneste ekstremum for denne funktion forekommer ved 
. Da 
for 
, er det mindste areal, der deles af tre ikke-primitive retvinklede trekanter, givet ved 
, hvilket resulterer i et areal på 840 og svarer til tripletterne (24, 70, 74), (40, 42, 58) og (15, 112, 113) (Beiler 1966, s. 126).
Højre trekanter, hvis areal består af et enkelt ciffer, omfatter 
(areal på 6) og 
(areal på 666666; Wells 1986, s. 89).
I 1643 udfordrede Fermat Mersenne til at finde en pythagoræisk triplet, hvis hypotenuse og summen af benene var kvadrater. Fermat fandt den mindste af disse løsninger:
 |
 |
 |
(41)
|
 |
 |
 |
(42)
|
 |
 |
 |
(43)
|
med
 |
 |
 |
(44)
|
 |
 |
 |
(45)
|
Et beslægtet problem er at bestemme, om et angivet heltal 
kan være arealet af en retvinklet trekant med rationelle sider. 1, 2, 3 og 4 er ikke arealet af nogen retvinklet trekant med rationelle sider, men 5 er det (3/2, 20/3, 41/6), ligesom 6 (3, 4, 5) er det. Løsningen på problemet involverer den elliptiske kurve
 |
(46)
|
En løsning (
, 
, 
) findes, hvis (46) har en rationel løsning, i hvilket tilfælde
 |
 |
 |
(47)
|
 |
 |
 |
(48)
|
(Koblitz 1993). Der findes ingen kendt generel metode til at bestemme, om der findes en løsning for vilkårlige 
, men en teknik udtænkt af J. Tunnell i 1983 gør det muligt at udelukke visse værdier (Cipra 1996).