Kemi for hovedfag

august 5, 2021
| Ingen kommentarer

Læringsresultater

  • Beskriv arrangementet af atomer og ioner i krystallinske strukturer
  • Beregne ionradier ved hjælp af celleenhedsdimensioner
  • Forklar brugen af X-strålediffraktionsmålinger til bestemmelse af krystallinske strukturer

Over 90 % af de naturligt forekommende og menneskeskabte faste stoffer er krystallinske. De fleste faste stoffer dannes med en regelmæssig placering af deres partikler, fordi de samlede tiltrækkende vekselvirkninger mellem partiklerne maksimeres, og den samlede intermolekylære energi minimeres, når partiklerne pakkes på den mest effektive måde. Det regelmæssige arrangement på atomart niveau afspejles ofte på makroskopisk niveau. I dette modul vil vi udforske nogle af detaljerne om strukturerne af metalliske og ioniske krystallinske faste stoffer og lære, hvordan disse strukturer bestemmes eksperimentelt.

Strukturerne af metaller

Vi vil begynde vores diskussion af krystallinske faste stoffer ved at betragte elementære metaller, som er relativt enkle, fordi de hver især kun indeholder én type atom. Et rent metal er et krystallinsk fast stof med metalatomer pakket tæt sammen i et gentagende mønster. Nogle af metallernes egenskaber generelt, f.eks. deres formbarhed og duktilitet, skyldes i høj grad, at de har identiske atomer anbragt i et regelmæssigt mønster. De forskellige egenskaber ved et metal i forhold til et andet metal afhænger delvist af størrelsen af deres atomer og de særlige forhold ved deres rumlige placering. Vi vil undersøge ligheder og forskelle mellem fire af de mest almindelige metalkrystalgeometrier i de følgende afsnit.

Metalers enhedsceller

Strukturen af et krystallinsk fast stof, uanset om det er et metal eller ej, beskrives bedst ved at betragte dets enkleste gentagende enhed, der betegnes som dets enhedscelle. Enhedscellen består af gitterpunkter, der repræsenterer atomernes eller ionernes placering. Hele strukturen består så af denne enhedscelle, der gentages i tre dimensioner, som illustreret i figur 1.

Der findes to tegninger. Til venstre er en terning gengivet med gitterpunkter i hvert hjørne og enhedsceller som sider. Til højre er den samme terning vist replikeret med en gråtonet skrifttype for at vise et uendeligt netværk af lignende terninger.

Figur 1. En enhedscelle viser placeringerne af gitterpunkter, der gentager sig i alle retninger.

Lad os begynde vores undersøgelse af krystalgitterstruktur og enhedsceller med den mest ligetil struktur og den mest grundlæggende enhedscelle. For at visualisere dette kan man forestille sig, at man tager et stort antal identiske kugler, f.eks. tennisbolde, og arrangerer dem ensartet i en beholder. Den enkleste måde at gøre dette på ville være at lave lag, hvor kuglerne i det ene lag ligger direkte over kuglerne i laget nedenunder, som illustreret i figur 2. Dette arrangement kaldes simpel kubisk struktur, og enhedscellen kaldes den simple kubiske enhedscelle eller primitive kubiske enhedscelle.

Tre tegninger af den samme terning fra 10.44. Til venstre er der tegnet cirkler omkring gitterpunkterne. I midten bliver disse gitterpunktscirkler til brune kugler, der pålægges kassen. Til højre ser vi den samme gengivelse af uendelige kasser som i 10.44.

Figur 2. Når metalatomer er anbragt med kugler i et lag direkte over eller under kugler i et andet lag, kaldes gitterstrukturen for simpel kubisk. Bemærk, at kuglerne er i kontakt.

I en simpel kubisk struktur er kuglerne ikke pakket så tæt, som de kunne være, og de “fylder” kun ca. 52% af beholderens volumen. Dette er et relativt ineffektivt arrangement, og kun ét metal (polonium, Po) krystalliserer i en simpel kubisk struktur. Som vist i figur 3 består et fast stof med denne type arrangement af planer (eller lag), hvor hvert atom kun kommer i kontakt med de fire nærmeste naboer i sit lag; et atom direkte over det i det øverste lag og et atom direkte under det i det nederste lag. Det antal andre partikler, som hver partikel i et krystallinsk fast stof har kontakt med, kaldes dets koordineringstal. For et poloniumatom i et simpelt kubisk felt er koordineringstallet derfor seks.

Der er vist to tegninger. Til venstre vises den uendelige stak af terninger fra 10.44, denne gang kun i sort og hvidt. Der er stor vægt på et gitterpunkt og de linjer, der støder umiddelbart op til det på kubikkanterne. Til højre vises den samme tegning, denne gang med gitterpunktet i rødt, og de udstrålende linjer fra dette punkt mærket 1-6.

Figur 3. Et atom i en simpel kubisk gitterstruktur har kontakt med seks andre atomer, så det har et koordinationsnummer på seks.

I et simpelt kubisk gitter er enhedscellen, der gentager sig i alle retninger, en terning defineret af centrene for otte atomer, som vist i figur 4. Atomer i tilstødende hjørner af denne enhedscelle kommer i kontakt med hinanden, så kantlængden af denne celle er lig med to atomradiusser eller en atomdiameter. En kubisk enhedscelle indeholder kun de dele af disse atomer, der befinder sig inden for den. Da et atom i et hjørne af en simpel kubisk enhedscelle er indeholdt af i alt otte enhedsceller, er kun en ottendedel af dette atom inden for en specifik enhedscelle. Og da hver enkelt kubisk enhedscelle har et atom i hvert af sine otte “hjørner”, er der 8 \ gange \frac{1}{8}=1 atom inden for en enkelt kubisk enhedscelle.

Der er vist to tegninger. Til venstre ses den kubiske enhed fra 10.45, med sfæriske grå molekyler overlejret over hvert gitterpunkt, mærket "simpel kubisk gittercelle". Til højre, mærket "8 hjørner", ses den samme kubiske enhed, der kun viser de dele af molekylernes kugler, der ville optræde inden for denne kubiske enhed.

Figur 4. En simpel kubisk gitter-enhedscelle indeholder en ottendedel af et atom i hvert af dens otte hjørner, så den indeholder et atom i alt.

Eksempel 1: Beregning af atomradius og tæthed for metaller, del 1

Kantlængden af enhedscellen for alfapolonium er 336 pm.

  1. Bestem radius for et poloniumatom.
  2. Bestem densiteten af alfapolonium.
Vis løsning

Alphapolonium krystalliserer i en simpel kubisk enhedscelle:

Et diagram viser en terning med en ottendedel af otte kugler inde i terningen, et afsnit i hvert hjørne. Langs den nederste højre side af kuben er der to dobbeltsidede pile, der hver strækker sig langs halvdelen af den samlede afstand på tværs af kuben. Hver pil er mærket
  1. To tilstødende Po-atomer berører hinanden, så kantlængden i denne celle er lig med to Po-atomradius: l=2r. Derfor er Po’s radius r=\dfrac{\text{l}}}{2}=\dfrac{\text{336 pm}}}{2}=\text{168 pm}.
  2. Densiteten er givet ved \text{densitet}=\dfrac{\text{masse}}}{\text{volumen}}. Poloniums densitet kan findes ved at bestemme densiteten af dets enhedscelle (massen indeholdt i en enhedscelle divideret med enhedscellens volumen). Da en Po-enhedscelle indeholder en ottendedel af et Po-atom i hvert af sine otte hjørner, indeholder en enhedscelle ét Po-atom.

Massen af en Po-enhedscelle kan findes ved:

\text{1 Po-enhedscelle}\times \dfrac{\text{1 Po-atom}}{\text{1 Po-enhedscelle}}\times \dfrac{\text{1 mol Po}}}{6.022\times {10}^{23}\text{Po atomer}}}\times \dfrac{208.998.998\text{g}}{\text{1 mol Po}}}=3.47\times {10}^{-22}\text{g}

Volumenet af en Po-enhedscelle kan findes ved:

V={l}^{3}={(336\times {10}^{-10}\text{cm})}^{3}=3.79\times {10}^{-23}{\text{cm}}}^{3}

(Bemærk, at kantlængden blev omregnet fra pm til cm for at få de sædvanlige volumenenheder for massefylde.)

Dermed er massefylden af \text{Po}=\dfrac{3.471\times {10}^{-22}\text{g}}}{3.79\times {10}^{-23}{\text{cm}}}^{3}}}={\text{9.16 g/cm}}}^{3}

Kontroller din læring

Kantlængden af enhedscellen for nikkel er 0,3524 nm. Densiteten af Ni er 8,90 g/cm3. Krystalliserer nikkel i en simpel kubisk struktur? Forklar.

Vis løsning

Nej. Hvis Ni var simpelt kubisk, ville dens massefylde være givet ved:

\text{1 Ni atom}\times \dfrac{\text{{1 mol Ni}}}{6.022\times {10}^{23}\text{Ni atomer}}}\times \dfrac{58.693\text{g}}{\text{1 mol Ni}}}=9.746\times {10}^{-23}\text{g}
V={l}^{3}={(3.524\times {10}^{-8}\text{cm})}^{3}=4.376\times {10}^{-23}{\text{cm}}}^{3}

Så vil densiteten af Ni være =\dfrac{9.746\times {10}^{-23}\text{g}}{4.376\times {10}^{-23}{\text{cm}}^{3}}}={\text{2.23 g/cm}}^{3}

Da den faktiske densitet af Ni ikke er tæt på dette, danner Ni ikke en simpel kubisk struktur.

De fleste metalkrystaller er en af de fire hovedtyper af enhedsceller. Indtil videre vil vi fokusere på de tre kubiske enhedsceller: den simple kubiske (som vi allerede har set), den kropscentrerede kubiske enhedscelle og den fladecentrerede kubiske enhedscelle – som alle er illustreret i figur 5. (Bemærk, at der faktisk findes syv forskellige gittesystemer, hvoraf nogle har mere end én type gitter, hvilket giver i alt 14 forskellige typer af enhedsceller. Vi lader de mere komplicerede geometrier være til senere i dette modul.)

Den første række af tegninger er mærket "gitterpunkts placering". Under den er der tre billeder. Til venstre ses den simple enhedskube med 6 gitterpunkter. I midten er en lidt større enhedskube med en rød prik i midten. Til højre er en endnu større kubisk enhed med 6 røde punkter indeni, arrangeret i to diagonale rækker af 3. Den nederste række af tegninger er mærket "Cubic unit cells". Til venstre ses den simple kubiske enhed med grå molekyler overlejret. I midten er den samme tegning, med et rødt molekyle centreret i kassen. Til højre er den samme tegning, med seks røde molekyler i 2 diagonale linjer inde i kassen.

Figur 5. Kubiske enhedsceller af metaller viser (i de øverste figurer) gitterpunkternes placering og (i de nederste figurer) metalatomerne placeret i enhedscellen.

Nogle metaller krystalliserer i et arrangement, der har en kubisk enhedscelle med atomer i alle hjørnerne og et atom i midten, som vist i figur 6. Dette kaldes et kropscentreret kubisk (BCC) fast stof. Atomer i hjørnerne af en BCC-enhedscelle har ikke kontakt med hinanden, men med atomet i midten. En BCC-enhedscelle indeholder to atomer: en ottendedel af et atom i hvert af de otte hjørner ( 8\ gange \frac{1}{8}=1 atom fra hjørnerne) plus et atom fra midten. Ethvert atom i denne struktur berører fire atomer i laget over det og fire atomer i laget under det. Et atom i en BCC-struktur har således et koordineringstal på otte.

Der vises tre tegninger. Til venstre ses den samme tegning af en kubisk enhed med en rød prik i midten, fra figur 10.48. I midten er den samme terning med grå molekyler overlejret, med et rødt molekyle i midten, som den nederste række i figur 10.48. Til venstre ses de dele af molekylerne uden for kuben barberet væk, og kun stykker af de grå molekyler og hele det røde molekyle er tilbage.

Figur 6. I en kropscentreret kubisk struktur rører atomerne i et bestemt lag ikke hinanden. Hvert atom berører fire atomer i laget over det og fire atomer i laget under det.

Atomer i BCC-arrangementer er meget mere effektivt pakket end i en simpel kubisk struktur, idet de optager ca. 68 % af det samlede volumen. Isomorfe metaller med en BCC-struktur omfatter K, Ba, Cr, Mo, W og Fe ved stuetemperatur. (Elementer eller forbindelser, der krystalliserer med samme struktur, siges at være isomorfe.)

Mange andre metaller, såsom aluminium, kobber og bly, krystalliserer i et arrangement, der har en kubisk enhedscelle med atomer i alle hjørner og i midten af hver side, som illustreret i figur 7. Denne opstilling kaldes et facetcentreret kubisk (FCC) fast stof. En FCC-enhedscelle indeholder fire atomer: en ottendedel af et atom i hvert af de otte hjørner (8\ gange \frac{1}{8}=1 atom fra hjørnerne) og et halvt atom på hver af de seks flader (6\ gange \frac{1}{2}=3 atomer fra fladerne). Atomerne i hjørnerne berører atomerne i midten af de tilstødende flader langs terningens diagonaler. Da atomerne befinder sig på identiske gitterpunkter, har de identiske miljøer.

Der vises tre tegninger. Til venstre ses den samme kubiske enhed med 6 røde prikker indeni, som i figur 10.48. I midten er den samme kubiske enhed med kugleformede molekyler overlejret, som i den nederste række i figur 10.48. Til højre er de grå molekyler, der er uden for kuben, barberet væk, så der kun er dele af de grå molekyler og seks halvdele af røde molekyler tilbage (da de blev delt i to).

Figur 7. Et facetcentreret kubisk fast stof har atomer i hjørnerne og, som navnet antyder, i midten af fladerne i dets enhedsceller.

Atomer i et FCC-arrangement er pakket så tæt sammen som muligt, idet atomerne optager 74 % af volumenet. Denne struktur kaldes også cubic closest packing (CCP). I CCP er der tre gentagende lag af hexagonalt arrangerede atomer. Hvert atom har kontakt med seks atomer i sit eget lag, tre i det øverste lag og tre i det nederste lag. I dette arrangement berører hvert atom 12 nære naboer og har derfor et koordineringstal på 12. Det er måske ikke umiddelbart indlysende, at FCC- og CCP-arrangementer er ækvivalente, men hvorfor de faktisk er den samme struktur, illustreres i figur 8.

Der er vist tre billeder. På det første billede ses i et sidebillede et lag af blå kugler, mærket

Figur 8. Et CCP-arrangement består af tre gentagende lag (ABCABC…) af hexagonalt arrangerede atomer. Atomer i en CCP-struktur har et koordineringstal på 12, fordi de har kontakt med seks atomer i deres lag plus tre atomer i laget over og tre atomer i laget under. Ved at dreje perspektivet kan vi se, at en CCP-struktur har en enhedscelle med en flade, der indeholder et atom fra lag A i det ene hjørne, atomer fra lag B på tværs af en diagonal (i to hjørner og i midten af fladen) og et atom fra lag C i det sidste hjørne. Dette er det samme som et ansigtcentreret kubisk arrangement.

Da tættere pakning maksimerer de samlede tiltrækninger mellem atomerne og minimerer den samlede intermolekylære energi, pakker atomerne i de fleste metaller på denne måde. Vi finder to typer af nærmeste pakning i simple metalliske krystallinske strukturer: CCP, som vi allerede har mødt, og hexagonal nærmeste pakning (HCP), som er vist i figur 9. Begge består af gentagne lag af hexagonalt arrangerede atomer. I begge typer er der et andet lag (B) placeret på det første lag (A), således at hvert atom i det andet lag er i kontakt med tre atomer i det første lag. Det tredje lag kan placeres på en af to måder. I HCP er atomerne i det tredje lag direkte over atomerne i det første lag (dvs. det tredje lag er også af type A), og stablingen består af skiftevis tætpakkede lag af type A og type B (dvs. ABABABAB⋯). I CCP er atomerne i det tredje lag ikke over atomerne i nogen af de to første lag (dvs. det tredje lag er af type C), og stablingen består af skiftende tætpakkede lag af type A, type B og type C (dvs. ABCABCABCABC⋯). Omkring to tredjedele af alle metaller krystalliserer i tætpakket lag med koordineringstal på 12. Metaller, der krystalliserer i en HCP-struktur, omfatter Cd, Co, Li, Mg, Na og Zn, og metaller, der krystalliserer i en CCP-struktur, omfatter Ag, Al, Ca, Cu, Ni, Pb og Pt.

Der er vist to billeder. Det første billede, der er mærket

Figur 9. I begge typer af nærmeste pakning er atomerne pakket så kompakt som muligt. Hexagonal nærmest pakning består af to skiftende lag (ABABABAB…). Cubic closest packing består af tre skiftende lag (ABCABCABCABC…).

Eksempel 2: Beregning af atomradius og tæthed for metaller, del 2

Calcium krystalliserer i en ansigtcentreret kubisk struktur. Kantlængden af dens enhedscelle er 558,8 pm.

  1. Hvad er atomradius for Ca i denne struktur?
  2. Beregn densiteten af Ca.
Vis løsning

Del 1

Der vises to tegninger. På den højre, "hexagonalt tættest pakket", ser vi et sidebillede af 4 rækker af kugler. Det øverste og tredje lag er grønne, mens det 2. og 4. lag er blå. På højre side, "cubic closest packed", ser vi et sidebillede af fire rækker af kugler. Den øverste og nederste række er blå (den øverste er mærket lag C). Den 2. række er grøn og betegnes lag B. Den tredje række er lilla og betegnes lag A.

I en FCC-struktur er Ca-atomer i kontakt med hinanden på tværs af diagonalen af fladen, så længden af diagonalen er lig med fire Ca-atomradius (d = 4r). To tilstødende kanter og fladens diagonal danner en retvinklet trekant, hvor længden af hver side er lig med 558,8 pm og længden af hypotenusen er lig med fire Ca-atomareradier:

{\text{a}}^{2}+{\text{a}}}^{2}={\text{d}}^{2}\longrightarrow {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}}}{16}}}=\text{197.6 pmg for en Ca radius}.

Del 2

Densiteten er givet ved \text{densitet}=\dfrac{\text{masse}}{{\text{volumen}}. Kalciums densitet kan findes ved at bestemme densiteten af dets enhedscelle: f.eks. massen indeholdt i en enhedscelle divideret med enhedscellens volumen. En fladecentreret Ca-enhedscelle har en ottendedel af et atom i hvert af de otte hjørner \left(8\times \dfrac{1}{8}=1\text{atom}\right) og et halvt atom på hver af de seks flader \left(6\times \dfrac{1}{2}=3\text{atomer}\right), dvs. i alt fire atomer i enhedscellen.

Massen af enhedscellen kan findes ved:

\text{1 Ca-enhedscelle}\times \dfrac{\text{4 Ca-atomer}}}{\text{1 Ca-enhedscelle}}\times \dfrac{\text{1 mol Ca}}{6.022\times {10}^{23}\text{Ca atomer}}}\times \dfrac{40.078\text{g}}{\text{1 mol Ca}}}=2.662\times {10}^{{-22}\text{g}

Volumenet af en Ca-enhedscelle kan findes ved:

V={a}^{3}={(558.8\times {10}^{-10}\text{cm})}^{3}=1.745\times {10}^{-22}{\text{cm}}}^{3}

(Bemærk, at kantlængden blev omregnet fra pm til cm for at få de sædvanlige volumenenheder for densitet.)

Så er densiteten af \text{Ca}=\dfrac{2.662\times {10}^{-22}\text{g}}}{1.745\times {10}^{-22}{\text{cm}}^{3}}}={\text{1.53 g/cm}}^{3}

Kontroller din læring

Sølv krystalliserer i en FCC-struktur. Kantlængden af dens enhedscelle er 409 pm.

  1. Hvad er atomradius for Ag i denne struktur?
  2. Beregne densiteten af Ag.
Vis løsninger

  1. 144 pm
  2. 10.5 g/cm3

Generelt er en enhedscelle defineret ved længderne af tre akser (a, b og c) og vinklerne (α, β og γ) mellem dem, som illustreret i figur 10. Akserne er defineret som værende længderne mellem punkterne i rumgitteret. Som følge heraf forbinder enhedscelleakser punkter med identiske miljøer.

Der er vist en tegning af en kubisk enhed med gitterpunkter. Planerne på terningens overflade er mærket a, b og c. Der vises en cirkel af pile omkring et gitterpunkt, mærket (α, β og γ).

Figur 10. En enhedscelle er defineret ved længderne af dens tre akser (a, b og c) og vinklerne (α, β og γ) mellem akserne.

Der findes syv forskellige gittesystemer, hvoraf nogle har mere end én type gitter, i alt 14 forskellige enhedsceller, som har de former, der er vist i figur 11.

En tabel med 7 rækker og to kolonner med titlerne System/Akser/Vinker og Enhedsceller.

Figur 11. Der findes syv forskellige gittesystemer og 14 forskellige enhedsceller.

Strukturer af ioniske krystaller

Ioniske krystaller består af to eller flere forskellige slags ioner, der normalt har forskellige størrelser. Pakningen af disse ioner i en krystalstruktur er mere kompleks end pakningen af metalatomer, der har samme størrelse.

De fleste monatomiske ioner opfører sig som ladede kugler, og deres tiltrækning af ioner med modsat ladning er den samme i alle retninger. Følgelig opstår stabile strukturer for ionforbindelser (1) når ioner med én ladning er omgivet af så mange ioner som muligt med modsat ladning, og (2) når kationer og anioner er i kontakt med hinanden. Strukturerne bestemmes af to hovedfaktorer: ionernes relative størrelse og forholdet mellem antallet af positive og negative ioner i forbindelsen.

Et billede viser et topbillede af et lag af blå kugler arrangeret i et ark, der ligger oven på et andet ark, der er det samme, bortset fra at kuglerne er grønne. Det andet ark er forskudt en lille smule, således at kuglerne i det øverste ark ligger i rillerne i det andet ark. Et tredje ark bestående af lilla kugler ligger i bunden. De mellemrum, der er skabt mellem kuglerne i hvert lag, er mærket

Figur 12. Kationer kan besætte to typer huller mellem anioner: oktaedriske huller eller tetraedriske huller.

I simple ionstrukturer finder vi normalt anionerne, som normalt er større end kationerne, anbragt i en tætpakket række. (Som tidligere set gør flere elektroner, der tiltrækkes til den samme kerne, anionerne større, og færre elektroner, der tiltrækkes til den samme kerne, gør kationerne mindre i forhold til de atomer, de er dannet af). De mindre kationer indtager almindeligvis en af de to typer huller (eller mellemrum), der er tilbage mellem anionerne. Det mindre af hullerne findes mellem tre anioner i et plan og en anion i et tilstødende plan. De fire anioner, der omgiver dette hul, er anbragt i hjørnerne af et tetraeder, så hullet kaldes et tetraedrisk hul. Den større type hul findes i midten af seks anioner (tre i ét plan og tre i et tilstødende plan) placeret i hjørnerne af et oktaeder; dette kaldes et oktaedrisk hul. Figur 12 illustrerer begge disse typer huller.

Afhængigt af de relative størrelser af kationerne og anionerne kan kationerne i en ionisk forbindelse indtage tetraedriske eller oktaedriske huller, som illustreret i figur 13. Relativt små kationer besætter tetraedriske huller, og større kationer besætter oktaedriske huller. Hvis kationerne er for store til at passe ind i de oktaedriske huller, kan anionerne antage en mere åben struktur, f.eks. en simpel kubisk række. De større kationer kan så indtage de større kubiske huller, der er muliggjort af den mere åbne afstand.

Der er givet tre gitterkubus-tegninger. Til venstre har den nederste venstre kubiske enhed grønne gitterpunkter, mens alle andre kuber har lilla punkter (mærket Tetrahedral hole). I midten er gitterpunkterne enten grønne eller orange, på en diagonal linje (mærket oktaedrisk hul). Til højre er alle gitterpunkterne lilla, mærket Kubisk hul.

Figur 13. En kations størrelse og formen af det hul, som forbindelsen besætter, hænger direkte sammen.

Der er to tetraedriske huller for hver anion i enten en HCP- eller CCP-anordning af anioner. En forbindelse, der krystalliserer i et tætpakket array af anioner med kationer i de tetraedriske huller, kan have et maksimalt kation:anion-forhold på 2:1; alle de tetraedriske huller er fyldt i dette forhold. Som eksempler kan nævnes Li2O, Na2O, Li2S og Na2S. Forbindelser med et forhold på mindre end 2:1 kan også krystallisere i et tætpakket array af anioner med kationer i de tetraedriske huller, hvis de ioniske størrelser passer. I disse forbindelser forbliver nogle af de tetraedriske huller dog ledige.

Eksempel 3: Besættelse af tetraedriske huller

Zinksulfid er en vigtig industriel kilde til zink og bruges også som hvidt pigment i maling. Zinksulfid krystalliserer med zinkioner, der besætter halvdelen af de tetraedriske huller i en tætpakket række af sulfidioner. Hvad er formlen for zinksulfid?

Vis løsning

Da der er to tetraedriske huller pr. anion (sulfidion), og halvdelen af disse huller er besat af zinkioner, skal der være \frac{1}{2}\ gange 2, eller 1, zinkion pr. sulfidion. Formlen er således ZnS.

Tjek din læring

Lithiumselenid kan beskrives som en tætpakket række af selenidioner med lithiumioner i alle de tetraedriske huller. Hvad er formlen for lithiumselenid?

Vis løsning

Li2Se

Forholdet mellem oktaedriske huller og anioner i enten en HCP- eller CCP-struktur er 1:1. Således kan forbindelser med kationer i oktaedriske huller i en tætest pakkede række af anioner have et maksimalt kation:anion-forhold på 1:1. I NiO, MnS, NaCl og KH er f.eks. alle de oktaedriske huller fyldt. Forhold på mindre end 1:1 observeres, når nogle af de oktaedriske huller forbliver tomme.

Eksempel 4: Støkiometri af ionforbindelser

Sapphire er aluminiumoxid. Aluminiumoxid krystalliserer med aluminiumioner i to tredjedele af de oktaedriske huller i en tættest pakket række af oxidioner. Hvad er formlen for aluminiumoxid?

Vis løsning

Da der er ét oktaedrisk hul pr. anion (oxidion), og kun to tredjedele af disse huller er besat, må forholdet mellem aluminium og oxygen være \frac{2}{3} :1, hvilket ville give {\text{Al}}}_{2\text{/}3}\text{O}. Det enkleste heltalsforhold er 2:3, så formlen er Al2O3.

Tjek din læring

Det hvide pigment titanoxid krystalliserer med titanioner i halvdelen af de oktaedriske huller i en tætpakket række af oxidioner. Hvad er formlen for titanoxid?

Vis løsning

TiO2

I et simpelt kubisk array af anioner er der ét kubisk hul, der kan være besat af et kation for hver anion i arrayet. I CsCl og i andre forbindelser med samme struktur er alle de kubiske huller besat. Halvdelen af de kubiske huller er besat i SrH2, UO2, SrCl2 og CaF2.

Differente typer af ionforbindelser krystalliserer ofte i samme struktur, når de relative størrelser af deres ioner og deres støkiometrier (de to hovedtræk, der bestemmer strukturen) er ens.

Enhedsceller for ioniske forbindelser

Mange ioniske forbindelser krystalliserer med kubiske enhedsceller, og vi vil bruge disse forbindelser til at beskrive de generelle træk ved ioniske strukturer.

Når en ionisk forbindelse er sammensat af kationer og anioner af samme størrelse i et 1:1-forhold, danner den typisk en simpel kubisk struktur. Cæsiumklorid, CsCl, (illustreret i figur 14) er et eksempel herpå, hvor Cs+ og Cl- har en radius på henholdsvis 174 pm og 181 pm. Vi kan betragte dette som kloridioner, der danner en simpel kubisk enhedscelle med en cæsiumion i midten; eller som cæsiumioner, der danner en enhedscelle med en kloridion i midten; eller som simple kubiske enhedsceller dannet af Cs+-ioner, der overlapper enhedsceller dannet af Cl-ioner. Cæsium- og kloridioner berører hinanden langs enhedscellernes diagonaler. Der er én cæsium-ion og én klorid-ion pr. enhedscelle, hvilket giver den stoiometri l:l, som kræves i formlen for cæsiumklorid. Bemærk, at der ikke er noget gitterpunkt i midten af cellen, og CsCl er ikke en BCC-struktur, fordi en cæsiumion ikke er identisk med en kloridion.

Der er vist tre tegninger. Til venstre ses en uendelig kubisk enhedsgengivelse, hvor den nederste venstre terning indeholder en rød prik i midten. I midten vises denne ene terning, med gitterpunkterne som store lilla kugler. Det centrale molekyle er mindre og grønt. Til højre vises en kube stak af lilla kugler, hvor små grønne kugler i mellem viser sig på den ene side.

Figur 14. Ioniske forbindelser med kationer og anioner af samme størrelse, som f.eks. CsCl, danner normalt en simpel kubisk struktur. De kan beskrives ved enhedsceller med enten kationer i hjørnerne eller anioner i hjørnerne.

Vi har sagt, at placeringen af gitterpunkterne er arbitrær. Dette illustreres af en alternativ beskrivelse af CsCl-strukturen, hvor gitterpunkterne er placeret i centrerne af cæsiumionerne. I denne beskrivelse er cæsiumionerne placeret på gitterpunkterne i cellens hjørner, og kloridionen er placeret i cellens centrum. De to enhedsceller er forskellige, men de beskriver identiske strukturer.

Når en ionisk forbindelse er sammensat af et 1:1 forhold mellem kationer og anioner, der adskiller sig væsentligt i størrelse, krystalliserer den typisk med en FCC-enhedscelle, som den, der er vist i figur 15. Natriumchlorid, NaCl, er et eksempel herpå, idet Na+ og Cl- har en radius på henholdsvis 102 pm og 181 pm. Vi kan se det som chloridioner, der danner en FCC-celle, med natriumioner placeret i de oktaedriske huller i midten af cellekanterne og i midten af cellen. Natrium- og kloridionerne berører hinanden langs cellekanterne. Enhedscellen indeholder fire natriumioner og fire kloridioner, hvilket giver den 1:1-støkiometri, som kræves af formlen, NaCl.

Der vises tre billeder. Det første billede viser en terning med sorte prikker i hvert hjørne og en rød prik i midten. Denne terning er stablet sammen med syv andre, der ikke er farvet, for at danne en større terning. Det andet billede består af otte kugler, der er grupperet sammen til en kube med en meget større kugle i midten. Navnet under dette billede lyder

Figur 15. Ioniske forbindelser med anioner, der er meget større end kationerne, som f.eks. NaCl, danner normalt en FCC-struktur. De kan beskrives ved FCC-enhedsceller med kationer i de oktaedriske huller.

Den kubiske form af zinksulfid, zinkblende, krystalliserer også i en FCC-enhedscelle, som illustreret i figur 16. Denne struktur indeholder sulfidioner på gitterpunkterne i et FCC-gitter. (Sulfidionernes placering er identisk med kloridionernes placering i natriumchlorid). Radius af en zinkion er kun ca. 40% af radius af en sulfidion, så disse små Zn2+-ioner er placeret i vekslende tetraedriske huller, dvs. i den ene halvdel af de tetraedriske huller. Der er fire zinkioner og fire sulfidioner i enhedscellen, hvilket giver den empiriske formel ZnS.

Der vises to tegninger. Til venstre gengives en uendelig kubisk struktur, hvor den nederste venstre terning indeholder seks røde prikker. Til højre er denne ene terning forstørret, og der vises gule prikker med tilfældige intervaller på kanterne og inde i terningen for at repræsentere gitterpunkter.

Figur 16. ZnS, zinksulfid (eller zinkblende) danner en FCC-enhedscelle med sulfidioner på gitterpunkterne og meget mindre zinkioner, der optager halvdelen af de tetraedriske huller i strukturen.

En calciumfluorid-enhedscelle, som den, der er vist i figur 17, er også en FCC-enhedscelle, men i dette tilfælde er kationerne placeret på gitterpunkterne; tilsvarende calciumioner er placeret på gitterpunkterne i et FCC-gitter. Alle tetraederpladserne i FCC-gitteret af calciumioner er besat af fluoridioner. Der er fire calciumioner og otte fluoridioner i en enhedscelle, hvilket giver et calcium:fluor-forhold på l:2, som det kræves i den kemiske formel CaF2. En nærmere undersøgelse af figur 17 afslører et simpelt kubisk felt af fluoridioner med calciumioner i den ene halvdel af de kubiske huller. Strukturen kan ikke beskrives ved hjælp af et rumgitter af punkter på fluoridionerne, fordi fluoridionerne ikke alle har identiske miljøer. Orienteringen af de fire calciumioner omkring fluoridionerne er forskellig.

Der vises to tegninger. Til venstre er der en uendelig kubisk strukturgengivelse, hvor den nederste venstre terning indeholder seks røde prikker. Til højre er denne ene terning forstørret, så den viser mange grønne kugler, i terningens hjørner og i det indre. Alle er forbundet med linjer. Mærket CaF2 face-centreret enhedscelle.

Figur 17. Calciumfluorid, CaF2, danner en FCC-enhedscelle med calciumioner (grønne) ved gitterpunkterne og fluoridioner (røde), der besætter alle tetraederpladserne imellem dem.

Beregning af ioniske radier

Hvis vi kender kantlængden af en enhedscelle i en ionisk forbindelse og ionernes placering i cellen, kan vi beregne ioniske radier for ionerne i forbindelsen, hvis vi gør antagelser om de enkelte ioners form og kontakter.

Eksempel 5: Beregning af ioniske radier

Kantlængden af enhedscellen for LiCl (NaCl-lignende struktur, FCC) er 0.514 nm eller 5,14 Å. Hvis man antager, at lithiumionen er tilstrækkelig lille til, at kloridionerne er i kontakt, som i figur 15, beregnes ionradius for kloridionen.

Note: Længdeenheden angstrom, Å, bruges ofte til at repræsentere dimensioner på atomskala og svarer til 10-10 m.

Vis løsning

På fladen af en LiCl-enhedscelle er chloridionerne i kontakt med hinanden på tværs af fladens diagonal:

Der vises tre billeder. Det første viser en terning af skiftevis grønne og lilla kugler. En mindre kube inden for denne kube er skitseret, og en større udgave af den vises derefter. Denne figur er en grå kube, der ser ud til at være sammensat af kugler. Der er små mellemrum mellem hver kugle. Der er en retvinklet trekant skitseret i denne kube, og en større version af den vises derefter. Denne retvinklede trekant har to sider mærket

Tegner man en retvinklet trekant på enhedscellens overflade, ser man, at diagonalens længde er lig med fire kloridradier (en radius fra hvert kloridhjørne og en diameter – som er lig med to radier – fra kloridionen i midten af overfladen), så d = 4r. Ud fra Pythagoras sætning har vi:

{\text{a}}}^{2}+{\text{a}}}^{2}={\text{d}}}^{2}

hvilket giver:

\left(0.514\text{ nm}}\right)^{2}+\left(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) for en Cl- radius

Kontroller din læring

Kantlængden af enhedscellen for KCl (NaCl-lignende struktur, FCC) er 6,28 Å. Hvis man antager anion-kation kontakt langs cellekanten, beregn da radius af kaliumionen. Kloridionens radius er 1,82 Å.

Vis løsning

Kaliumionens radius er 1,33 Å.

Det er vigtigt at være klar over, at værdier for ionradier beregnet ud fra enhedscellers kantlængder afhænger af talrige antagelser, såsom en perfekt sfærisk form for ioner, som i bedste fald er tilnærmelser. Derfor er sådanne beregnede værdier i sig selv tilnærmede, og sammenligninger kan ikke skubbes for langt frem. Ikke desto mindre har denne metode vist sig nyttig til beregning af ionradier ud fra eksperimentelle målinger som f.eks. røntgenkrystallografiske bestemmelser.

Røntgenkrystallografi

Størrelsen af enhedscellen og atomernes arrangement i en krystal kan bestemmes ud fra målinger af diffraktion af røntgenstråler ved krystallen, såkaldt røntgenkrystallografi. Diffraktion er den ændring i den retning, som en elektromagnetisk bølge oplever, når den støder på en fysisk barriere, hvis dimensioner svarer til lysets bølgelængde. Røntgenstråler er elektromagnetisk stråling med bølgelængder, der er omtrent lige så lange som afstanden mellem naboatomer i krystaller (i størrelsesordenen nogle få Å).

Når en stråle af monokromatiske røntgenstråler rammer en krystal, spredes dens stråler i alle retninger af atomerne i krystallen. Når spredte bølger, der bevæger sig i samme retning, møder hinanden, undergår de interferens, en proces, hvorved bølgerne kombineres for at give enten en forøgelse eller et fald i amplitude (intensitet) afhængigt af, i hvilket omfang de kombinerende bølgers maksima er adskilt (se figur 18).

Der er vist et billedpar, der har fire sektioner. I det første afsnit vises to sinusformede bølger, den ene er tegnet over den anden, og et afsnit fra toppen af den ene kurve til toppen af den næste kurve er mærket

Figur 18. Lysbølger, der optager samme rum, oplever interferens, idet de kombineres og giver bølger af større (a) eller mindre (b) intensitet, afhængigt af afstanden mellem deres maksima og minima.

Når røntgenstråler med en bestemt bølgelængde, λ, spredes af atomer i tilstødende krystalplaner, der er adskilt af en afstand, d, kan de undergå konstruktiv interferens, når forskellen mellem de afstande, som de to bølger har tilbagelagt før deres kombination, er en heltalsfaktor, n, af bølgelængden. Denne betingelse er opfyldt, når vinklen af den diffrakterede stråle, θ, er relateret til bølgelængden og den interatomare afstand ved ligningen:

n{\lambda }=2d\text{sin}\theta

Denne relation er kendt som Bragg-ligningen til ære for W. H. Bragg, den engelske fysiker, der først forklarede dette fænomen. Figur 19 illustrerer to eksempler på diffrakterede bølger fra de samme to krystalplaner. Figuren til venstre viser bølger, der diffrakteres i Bragg-vinklen, hvilket resulterer i konstruktiv interferens, mens figuren til højre viser diffraktion og en anden vinkel, der ikke opfylder Bragg-betingelsen, hvilket resulterer i destruktiv interferens.

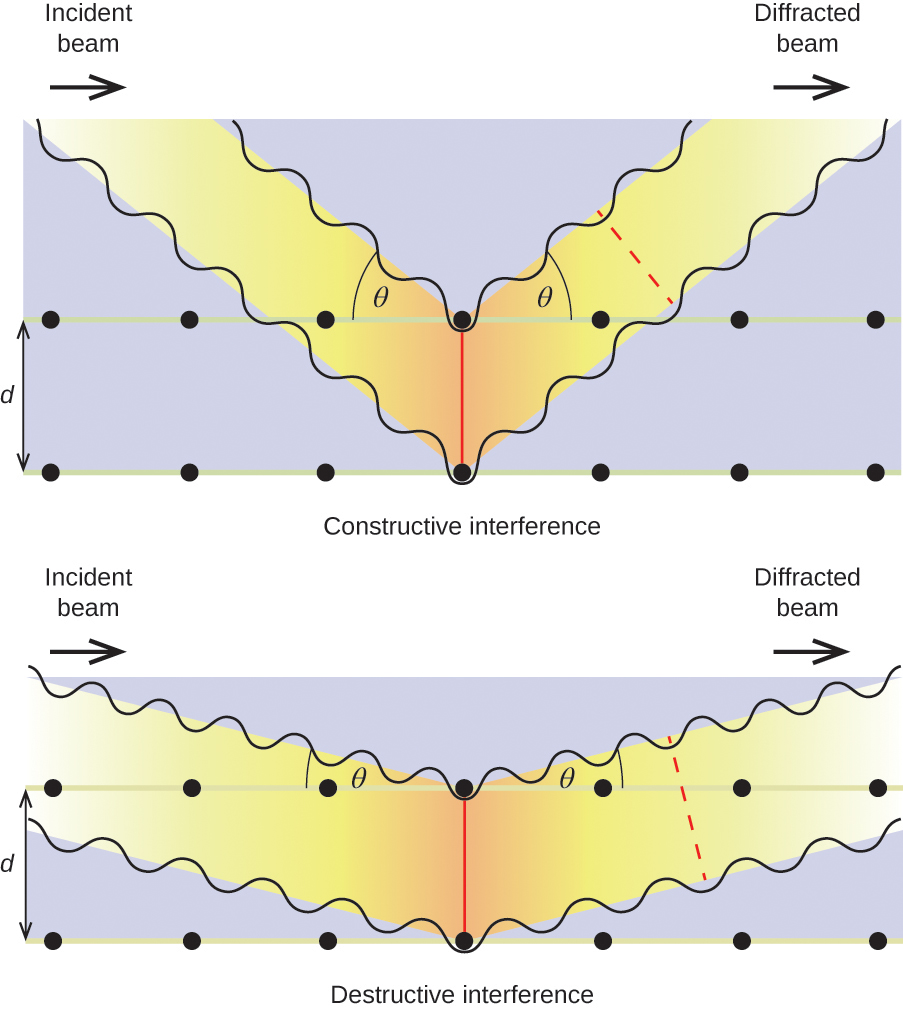
Der er vist to lignende figurer. Den første figur, der er mærket

Figur 19. Diffraktion af røntgenstråler, der spredes af atomerne i en krystal, gør det muligt at bestemme afstanden mellem atomerne. Det øverste billede viser konstruktiv interferens mellem to spredte bølger og en resulterende diffrakteret bølge af høj intensitet. Det nederste billede viser destruktiv interferens og en diffrakteret bølge med lav intensitet.

Se “Hvad er Braggs lov, og hvorfor er den vigtig?” for at få flere oplysninger om Bragg-ligningen og en simulator, der giver dig mulighed for at undersøge virkningen af de enkelte variabler på intensiteten af den diffrakterede bølge.

Et røntgendiffraktometer som det, der er illustreret i figur 20, kan anvendes til at måle de vinkler, som røntgenstråler bliver diffrakteret, når de interagerer med en krystal som beskrevet ovenfor. Ud fra sådanne målinger kan Bragg-ligningen anvendes til at beregne afstandene mellem atomerne som vist i følgende eksempeløvelse.

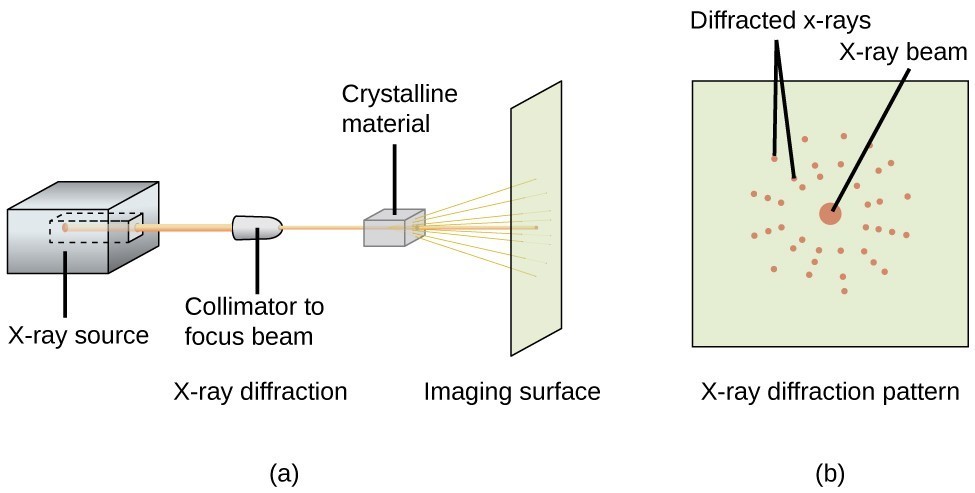
Der gives to sæt tegninger. Til højre, a) er et sidebillede af en projiceret røntgenstråle fra en maskine mod væggen, der passerer gennem et krystallinsk materiale. Til højre, b) er et frontalt billede af væggen, der viser røntgenstrålen og de diffrakterede røntgenstråler, der er resultatet.

Figur 20. I et diffraktometer (a) rammer en stråle af røntgenstråler et krystallinsk materiale og frembringer et røntgendiffraktionsmønster (b), som kan analyseres for at bestemme krystalstrukturen.

Du kan se transskriptionen til “Celebrating Crystallography – An animated adventure” her (åbner i nyt vindue).

Eksempel 6: Brug af Bragg-ligningen

I et diffraktometer blev der brugt røntgenstråler med en bølgelængde på 0,1315 nm til at fremstille et diffraktionsmønster for kobber. Første ordens diffraktion (n = 1) opstod ved en vinkel θ = 25,25°. Bestem afstanden mellem de diffrakterende planer i kobber.

Vis løsning

Afstanden mellem planerne findes ved at løse Bragg-ligningen, nλ = 2d sin θ, for d.

Dette giver: d=\dfrac{n\lambda}{2\sin\theta}=\dfrac{1\left(0.1315\text{ nm}\right)}{2\sin\left(25.25^{\circ}\right)}=0.154\text{ nm}

Tjek din læring

En krystal med en afstand mellem planerne lig med 0.394 nm diffrakterer røntgenstråler med en bølgelængde på 0.147 nm. Hvad er vinklen for første ordens diffraktion?

Vis løsning

10,8°

Portræt af en kemiker: Røntgenkrystallograf Rosalind Franklin

Et billede viser en cirkulær illustration med ringe af prikker, der er sløret sammen.

Figur 21. Denne illustration viser et røntgendiffraktionsbillede, der ligner det, som Franklin fandt i sin forskning. (credit: National Institutes of Health)

Den opdagelse af DNA’s struktur, som Francis Crick og James Watson gjorde i 1953, er en af de store bedrifter i videnskabshistorien. De fik i 1962 Nobelprisen i fysiologi eller medicin sammen med Maurice Wilkins, som leverede det eksperimentelle bevis for DNA’s struktur. Den britiske kemiker Rosalind Franklin ydede et uvurderligt bidrag til denne monumentale bedrift gennem sit arbejde med at måle røntgendiffraktionsbilleder af DNA. Tidligt i sin karriere viste Franklins forskning i kuls struktur sig at være nyttig for den britiske krigsindsats. Efter at have flyttet sit fokus til biologiske systemer i begyndelsen af 1950’erne opdagede Franklin og ph.d.-studerende Raymond Gosling, at DNA består af to former: en lang, tynd fiber, der dannes, når den er våd (type “B”), og en kort, bred fiber, der dannes, når den tørres (type “A”). Hendes røntgendiffraktionsbilleder af DNA (figur 21) gav de afgørende oplysninger, der gjorde det muligt for Watson og Crick at bekræfte, at DNA danner en dobbeltspiral, og at bestemme detaljerne i dets størrelse og struktur.

Franklin udførte også banebrydende forskning om virus og det RNA, der indeholder deres genetiske information, og afdækkede nye oplysninger, der radikalt ændrede vidensgrundlaget inden for området. Efter at have udviklet kræft i æggestokkene fortsatte Franklin med at arbejde indtil sin død i 1958 i en alder af 37 år. Blandt mange posthume anerkendelser af hendes arbejde ændrede Chicago Medical School of Finch University of Health Sciences sit navn til Rosalind Franklin University of Medicine and Science i 2004 og vedtog et billede af hendes berømte røntgendiffraktionsbillede af DNA som sit officielle universitetslogo.

Nøglebegreber og resumé

Strukturen af krystallinske metaller og simple ionforbindelser kan beskrives i form af pakninger af kugler. Metalatomer kan pakke sig i hexagonale nærmest-pakkede strukturer, kubiske nærmest-pakkede strukturer, kropscentrerede strukturer og simple kubiske strukturer. Anionerne i simple ioniske strukturer antager almindeligvis en af disse strukturer, og kationerne indtager de resterende rum mellem anionerne. Små kationer indtager sædvanligvis tetraedriske huller i en tætest pakkede række af anioner. Større kationer optager normalt oktaedriske huller. Endnu større kationer kan indtage kubiske huller i en simpel kubisk række af anioner. Et fast stofs struktur kan beskrives ved at angive størrelsen og formen af en enhedscelle og cellens indhold. Enhedscellens strukturtype og dimensioner kan bestemmes ved hjælp af røntgendiffraktionsmålinger.

Nøgleligninger

  • n{\lambda }=2d\text{sin}\theta

Forsøg det

  1. Beskriv krystalstrukturen for jern, som krystalliserer med to tilsvarende metalatomer i en kubisk enhedscelle.
  2. Beskriv krystalstrukturen for Pt, som krystalliserer med fire ækvivalente metalatomer i en kubisk enhedscelle.
  3. Hvad er koordineringstallet for et kromatom i den kropscentrerede kubiske struktur for krom?
  4. Hvad er koordineringstallet for et aluminiumatom i den ansigtcentrerede kubiske struktur for aluminium?
  5. Koboltmetallet krystalliserer i en hexagonal tættest pakket struktur. Hvad er koordineringstallet for et koboltatom?
  6. Nikkelmetal krystalliserer i en kubisk nærmest pakkede struktur. Hvad er koordinationsnummeret for et nikkelatom?
  7. Volfram krystalliserer i en kropscentreret kubisk enhedscelle med en kantlængde på 3,165 Å.
    1. Hvad er atomradius for wolfram i denne struktur?
    2. Beregn tætheden af wolfram.
  8. Platin (atomradius = 1,38 Å) krystalliserer i en kubisk tætpakket struktur. Beregn kantlængden af den ansigtcentrerede kubiske enhedscelle og tætheden af platin.
  9. Barium krystalliserer i en kropscentreret kubisk enhedscelle med en kantlængde på 5.025 Å
    1. Hvad er atomradius for barium i denne struktur?
    2. Beregn densiteten af barium.
  10. Aluminium (atomradius = 1,43 Å) krystalliserer i en kubisk tætpakket struktur. Beregn kantlængden af den ansigtcentrerede kubiske enhedscelle og tætheden af aluminium.
  11. Tætheden af aluminium er 2,7 g/cm3; den af silicium er 2,3 g/cm3. Forklar, hvorfor Si har den lavere massefylde, selv om det har tungere atomer.
  12. Det frie rum i et metal kan findes ved at trække volumenet af atomerne i en enhedscelle fra cellens volumen. Beregn den procentvise andel af det frie rum i hvert af de tre kubiske gitter, hvis alle atomer i hvert gitter er lige store og berører deres nærmeste naboer. Hvilken af disse strukturer repræsenterer den mest effektive pakning? Det vil sige, hvilken pakning har mindst uudnyttet plads?
  13. Cadmiumsulfid, der undertiden anvendes som et gult pigment af kunstnere, krystalliserer med cadmium, der optager halvdelen af de tetraedriske huller i en tættest pakket række af sulfidioner. Hvad er formlen for cadmiumsulfid? Forklar dit svar.
  14. En forbindelse af cadmium, tin og fosfor anvendes til fremstilling af nogle halvledere. Den krystalliserer med cadmium, der optager en fjerdedel af de tetraedriske huller, og tin, der optager en fjerdedel af de tetraedriske huller i en tættest pakket række af fosfidioner. Hvilken formel har denne forbindelse? Forklar dit svar.
  15. Hvad er formlen for det magnetiske oxid af kobolt, der anvendes i optagebånd, og som krystalliserer med koboltatomer, der besætter en ottendedel af de tetraedriske huller og en halvdel af de oktaedriske huller i en tætpakket række af oxidioner?
  16. En forbindelse, der indeholder zink, aluminium og svovl, krystalliserer med en tætpakket række af sulfidioner. Zinkioner findes i en ottendedel af de tetraedriske huller og aluminiumioner i halvdelen af de oktaedriske huller. Hvad er den empiriske formel for forbindelsen?
  17. En forbindelse af thallium og jod krystalliserer i en simpel kubisk række af jodidioner med thalliumioner i alle de kubiske huller. Hvad er formlen for dette jodid? Forklar dit svar.
  18. Hvilket af følgende grundstoffer reagerer med svovl og danner et fast stof, hvor svovlatomerne danner et tætpakket felt med alle de oktaedriske huller besat: Li, Na, Be, Ca eller Al?
  19. Hvad er masseprocenten af titan i rutil, et mineral, der indeholder titan og ilt, hvis strukturen kan beskrives som en tætpakket række af oxidioner med titanioner i halvdelen af de oktaedriske huller? Hvad er titans oxidationstal?
  20. Forklar, hvorfor de kemisk ens alkalimetallklorider NaCl og CsCl har forskellige strukturer, mens de kemisk forskellige NaCl og MnS har den samme struktur.
  21. Da mineraler blev dannet fra den smeltede magma, besatte forskellige ioner de samme pladser i krystallerne. Lithium forekommer ofte sammen med magnesium i mineraler på trods af forskellen i ladningen på deres ioner. Foreslå en forklaring.
  22. Rubidiumjodid krystalliserer med en kubisk enhedscelle, der indeholder jodidioner i hjørnerne og en rubidiumion i midten. Hvad er forbindelsens formel?
  23. Et af de forskellige manganoxider krystalliserer med en kubisk enhedscelle, der indeholder manganioner i hjørnerne og i midten. Oxidionerne er placeret i midten af hver kant af enhedscellen. Hvilken formel har denne forbindelse?
  24. NaH krystalliserer med samme krystalstruktur som NaCl. Kantlængden af den kubiske enhedscelle for NaH er 4,880 Å.
    2. Beregn ionradius for H-. (Li+’s ionradius er 0,0,95 Å.)
    3. Beregn tætheden af NaH.
  25. Thallium(I)-jodid krystalliserer med samme struktur som CsCl. Kantlængden af enhedscellen for TlI er 4,20 Å.
    1. Beregn ionradius for TI+. (Ionradius for I- er 2,16 Å.)
    2. Beregn tætheden af TlI.
  26. En kubisk enhedscelle indeholder manganioner i hjørnerne og fluoridioner i midten af hver kant.
    1. Hvad er den empiriske formel for denne forbindelse? Forklar dit svar.
    2. Hvad er Mn3+-ionens koordinationsnummer?
    3. Beregn kantlængden af enhedscellen, hvis radius af en Mn3+-ion er 0,65 A.
    4. Beregn densiteten af forbindelsen.
  27. Hvad er afstanden mellem de krystalplaner, der diffrakterer røntgenstråler med en bølgelængde på 1,541 nm i en vinkel θ på 15,55° (første ordens refleksion)?
  28. Et diffraktometer, der anvender røntgenstråler med en bølgelængde på 0,2287 nm, frembragte første ordens diffraktionstoppen for en krystalvinkel θ = 16,21°. Bestem afstanden mellem de diffrakterende planer i denne krystal.
  29. Et metal med en afstand mellem planerne på 0,4164 nm diffrakterer røntgenstråler med en bølgelængde på 0,2879 nm. Hvad er diffraktionsvinklen for første ordens diffraktionstoppen?
  30. Guld krystalliserer i en ansigtcentreret kubisk enhedscelle. Andenordensrefleksionen (n = 2) af røntgenstråler for de planer, der udgør toppen og bunden af enhedscellerne, ligger ved θ = 22,20°. Bølgelængden af røntgenstrålerne er 1,54 Å. Hvad er tætheden af metallisk guld?
  31. Når en elektron i et exciteret molybdænatom falder fra L til K-skallen, udsendes der en røntgenstråle. Disse røntgenstråler diffrakteres i en vinkel på 7,75° af planer med en afstand på 2,64 Å. Hvad er energiforskellen mellem K- og L-skallen i molybdæn, hvis man antager en første ordens diffraktion?
Vis udvalgte løsninger

1. Strukturen af denne lavtemperatursform af jern (under 910 °C) er kropscentreret kubisk. Der er et ottendedels atom i hvert af de otte hjørner af kuben og et atom i kubens centrum.

3. Koordineringstallet henviser til antallet af nærmeste naboer. Et kromatom ligger i centrum af en kropscentreret terning og har otte nærmeste naboer (ved terningens hjørner): fire i et plan over og fire i et plan under. Koordineringstallet er derfor otte.

5. Hexagonal nærmeste pakning sker på en sådan måde, at hvert atom berører 12 nærmeste naboer: 6 i sit eget lag og 3 i hvert tilstødende lag. Koordineringstallet er derfor 12.

7. (a) I en kropscentreret kubisk enhedscelle er metalatomerne i kontakt langs den indre diagonal af terningen. Den indvendige diagonal danner en retvinklet trekant med enhedscellekanten og fladens diagonal. Brug den pythagoræiske sætning til at bestemme længden af diagonalen, d, på kubens flade i forhold til kanten, e.

d2 = e2 + e2 = 2e2

d = \sqrt{2} e

Den indre diagonal i kuben er længden af fire atomradier og kan beregnes igen ved at bruge den pythagoræiske sætning og fladens diagonal og kant.

\begin{array}{rll}\left(\text{diagonal}\right)^2&=&d^2+e^2 \\\ &=& \left(\sqrt{2} e\right)+e^2 \\ &=& 2e^2+e^2 \\ &=&3e^2 \\ \text{diagonal}&=&\sqrt{3}e=4r\end{array}

Radius af wolfram = \frac{\text{diagonal}}}{4}=\frac{\sqrt{3}e}{4}=\frac{\sqrt{3}}}{4}\ venstre(3.165\mathring{\text{A}}\right)=1.370\mathring{\text{A}}};

(b) Givet den kropscentrerede kubiske struktur, indeholder hver enhedscelle to atomer. Brug enhedscellens kantlængde til at beregne enhedscellens volumen og det volumen, som hvert atom optager. Multiplicer for at få det molare volumen og divider atommassen med denne værdi for at få densiteten (e = kantlængde):

V(celle) = e3 = (3,165 \times 10-8 cm)3 = 3,170 \times 10-23 cm3

V(atom) = \frac{3,170\times {10}^{-23}{\text{cm}}}^{3}}}{\text{2 atomer}}}=1.585\times {10}^{-23}{\text{cm}}}^{3}{\text{atom}}}^{-1}

V(mol) = 1.585 \times 10-23 cm3/atom \times 6.022 \times 1023 atomer/mol

= 9.546 cm3/mol

densitet = \frac{183.85{{\text{g mol}}^{-1}}}{9.546{\text{cm}}^{3}{\text{mol}}}^{-1}}} = 19.26 g/cm

9. (a) I en kropscentreret kubisk enhedscelle er metalatomerne i kontakt langs kubens diagonal. Kubens diagonal danner en retvinklet trekant med enhedscellens kant og diagonalen i en flade. Brug Pythagoras sætning til at bestemme længden af diagonalen, d, på terningens flade i forhold til e.

d2 = e2 + e2 = 2e2

d = \sqrt{2} e

Diagonalen på terningen er længden af fire atomare radier og kan beregnes ved igen at bruge pythagoras’ sætning:

(diagonal)2 = (4r)2 = (2e)2 + e2 = 16r2 = 3e2

diagonal = 4r = \sqrt{3\text{e}}}

r = \frac{\sqrt{3}}}{4}\text{e}}=\frac{\sqrt{3}}}{4} (5,025 Å) = 2,176 Å;

(b) Givet en kubisk struktur med kropscentreret kubisk struktur, indeholder hver enhedscelle to atomer. Brug enhedscellens kantlængde til at beregne enhedscellens volumen og det volumen, som hvert atom optager. Multiplicer for at få det molare volumen, og divider gramm atomvægt med denne værdi for at få massefylde (e = kantlængde):

V (celle) = e3 = (5,025 \ gange 10-8 cm)3 = 1,26884 \ gange 10-22 cm3

V (atom) = 1.26884 \times \frac{{{10}^{-22}{\text{cm}}}^{3}{\text{atom}}^{\text{-1}}}}{\text{2 atomer}}} = 6.3442 \times 10-23 cm3

V (mol) = 6.3442 \times 10-23 cm3 \times 6.022 \times 1023 atomer/mol = 38.205 cm3

d(Ba) = \frac{137.33 g}{38.204 cm}^{3} = 3.595 g/cm3

11. Si’s krystalstruktur viser, at det er mindre tæt pakket (koordinationsnummer 4) i det faste stof end Al (koordinationsnummer 12).

13. I et tætpakket felt findes der to tetraedriske huller for hver anion. Hvis kun halvdelen af de tetraedriske huller er besat, er antallet af anioner og kationer lige stort. Formlen for cadmiumsulfid er CdS.

15. I et tætpakket felt af oxidioner findes der et oktaedrisk hul og to tetraedriske huller for hver oxidion. Hvis halvdelen af de oktaedriske huller er fyldt, er der en Co-ion for hver to oxidioner. Hvis en ottendedel af de tetraedriske huller er fyldt, er der en Co-ion for hver fire oxidioner. For hver fire oxidioner er der to Co-ioner i oktaedriske huller og én Co-ion i et tetraedrisk hul; formlen er således Co3O4.

17. I et simpelt kubisk felt kan kun ét kubisk hul være besat af en kation for hver anion i feltet. Forholdet mellem thallium og jodid skal være 1:1; derfor er formlen for thallium TlI.

19. Forholdet mellem oktaedriske huller og iltanioner er 1:1 i en tætest pakkede matrix. Kun halvdelen af de oktaedriske huller er besat. Forholdet mellem titan og ilt er således 1:2, og formlen er TiO2. Masseprocenten af Ti i strukturen er:

procent Ti = \frac{47,90}{47,90+\text{2(15,9994)}}}\times \text{100%}=\text{59,95%}

Oxidationstallet for titan er +4, fordi der er to O2-ioner for hver Ti-ion.

21. Begge ioner er tæt på hinanden i størrelse: Mg, 0,65; Li, 0,60. Denne lighed gør det muligt for de to at udveksle dem ret let. Forskellen i ladning kompenseres generelt ved at skifte Si4+ ud med Al3+.

23. Det samlede antal Mn-ioner bestemmes ved at lægge bidragene fra hjørnerne og midten sammen. Mn (hjørner): 8 \ gange \frac{1}{8}; Mn (centrum) = 1. Samlet Mn-bidrag til enhedscellen = 2.

For O er der i alt 12 kanter i terningen, og hver ion i kanten bidrager med en fjerdedel til enhedscellen. Følgelig er der 12 \ gange \frac{1}{4} = 3 O-atomer. Forholdet er Mn:O = 2:3, og formlen er Mn2O3.

27. Bragg-ligningen er: nλ = 2d sin θ

hvor d er afstanden mellem planerne.

d = \frac{n{\lambda }}{\text{2 sin}\theta }=\frac{1(1.541 A)}{2\sin15.55^{\circ}}}=\frac{1.541\mathring{\text{A}}}}{2(0.2681)} = 2.874 Å

29. \text{sin}\theta =\frac{n{\lambda }}{2d}=\frac{1)(0.2879\text{nm})}{(2)(0.4164)}=0.3457, så θ = sin-1(0.3457) = 20.2°

31. Brug Bragg-ligningen, hvor n = 1,

λ = 2dsinθ =2(2,64 Å)sin 7,75 = 0,712 Å

Så er E=\frac{hc}{\lambda}=\frac{(6.626\times {10}^{-34}\text{J s})(2.998\times {10}^{8}{\text{m s}}}^{-1})}{0.712\times {10}^{-10}\text{m}}} =2.79\times {10}^{-15}\text{J}=1.74\times {10}^{4}\text{eV}

Glossar

kropscentreret kubisk (BCC) faststof: krystallinsk struktur, der har en kubisk enhedscelle med gitterpunkter i hjørnerne og i midten af cellen

kropscentreret kubisk enhedscelle: Den enkleste gentagende enhed i en kropscentreret kubisk krystal; det er en terning med gitterpunkter i hvert hjørne og i midten af terningen

Bragg-ligning: ligning, der relaterer de vinkler, hvormed røntgenstråler diffrakteres af atomerne i en krystal

koordineringsnummer: antal atomer, der er tættest på et givet atom i en krystal eller på det centrale metalatom i et kompleks

cubic closest packing (CCP): struktur med en kubisk tæteste pakning: krystallinsk struktur, hvor planer af tæt pakkede atomer eller ioner er stablet som en serie af tre vekslende lag med forskellige relative orienteringer (ABC)

diffraktion: Omdirigering af elektromagnetisk stråling, der sker, når den møder en fysisk barriere af passende dimensioner

fladecentreret kubisk (FCC) fast stof: krystallinsk struktur bestående af en kubisk enhedscelle med gitterpunkter på hjørnerne og i midten af hver flade

fladecentreret kubisk enhedscelle: Det er en terning med gitterpunkter i hvert hjørne og i midten af hver side

hexagonal closest packing (HCP): krystallinsk struktur, hvor tætpakkede lag af atomer eller ioner er stablet som en serie af to skiftende lag med forskellige relative orienteringer (AB)

hul: krystallinsk struktur, hvor tætpakkede lag af atomer eller ioner er stablet som en serie af to skiftende lag med forskellige relative orienteringer (AB)

hul: (også, interstice) rum mellem atomer i en krystal

isomorft: besidder samme krystalstruktur

oktaedrisk hul: åbent rum i en krystal i midten af seks partikler placeret i hjørnerne af et oktaeder

en simpel kubisk enhedscelle: (også primitiv kubisk enhedscelle) enhedscelle i den simple kubiske struktur

impel kubisk struktur: krystalstruktur med en kubisk enhedscelle med gitterpunkter kun i hjørnerne

rumsgitter: alle punkter i en krystal, der har identiske miljøer

tetraedrisk hul: tetraedrisk rum dannet af fire atomer eller ioner i en krystal

enhedscelle: mindste del af et rumgitter, der gentages i tre dimensioner for at danne hele gitteret

røntgenkrystallografi: eksperimentel teknik til bestemmelse af afstandene mellem atomerne i en krystal ved at måle de vinkler, hvormed røntgenstråler bliver diffrakteret, når de passerer gennem krystallen

Articles