I det syttende og især det attende århundrede, drevet både af et ønske om at forstå naturen og en stræben efter at lave balloner, som de kunne flyve i (figur 1), etablerede en række videnskabsmænd sammenhængen mellem gassers makroskopiske fysiske egenskaber, dvs. tryk, volumen, temperatur og gasmængde. Selv om deres målinger ikke var præcise efter nutidens standarder, var de i stand til at bestemme de matematiske sammenhænge mellem par af disse variabler (f.eks. tryk og temperatur, tryk og volumen), der gælder for en idealgas – en hypotetisk konstruktion, som virkelige gasser nærmer sig under visse betingelser. Til sidst blev disse individuelle love kombineret til en enkelt ligning – den ideelle gaslov – som relaterer gasmængder for gasser og er ret præcis ved lave tryk og moderate temperaturer. Vi vil se på de vigtigste udviklinger i de enkelte forhold (af pædagogiske årsager ikke helt i historisk rækkefølge) og derefter sætte dem sammen i loven for den ideelle gas.

Figur 1. I 1783 fandt den første (a) brintfyldte ballonflyvning, (b) bemandede varmluftballonflyvning og (c) bemandede brintfyldte ballonflyvning sted. Da den brintfyldte ballon, der er afbildet i (a), landede, ødelagde de forskrækkede landsbyboere i Gonesse den efter sigende med høtyve og knive. Opsendelsen af den sidstnævnte blev efter sigende set af 400.000 mennesker i Paris.

Tryk og temperatur: Gay-Lussacs lov

Forestil dig, at du fylder en stiv beholder, der er fastgjort til en trykmåler, med gas og derefter forsegler beholderen, så ingen gas kan slippe ud. Hvis beholderen afkøles, bliver gassen indeni ligeledes koldere, og man observerer, at dens tryk falder. Da beholderen er stiv og tæt forseglet, forbliver både volumen og antal mol af gas konstant. Hvis man opvarmer kuglen, bliver gassen indeni varmere (figur 2), og trykket stiger.

Figur 2. Temperaturens virkning på gastrykket: Når varmepladen er slukket, er trykket af gassen i kuglen relativt lavt. Når gassen opvarmes, stiger trykket af gassen i kuglen.

Dette forhold mellem temperatur og tryk observeres for enhver prøve af gas, der er indesluttet i et konstant volumen. Et eksempel på eksperimentelle tryk-temperaturdata er vist for en luftprøve under disse betingelser i figur 3. Vi finder, at temperatur og tryk hænger lineært sammen, og hvis temperaturen er på kelvinskalaen, er P og T direkte proportionale (igen, når volumen og mol af gas holdes konstant); hvis temperaturen på kelvinskalaen stiger med en vis faktor, stiger gastrykket med den samme faktor.

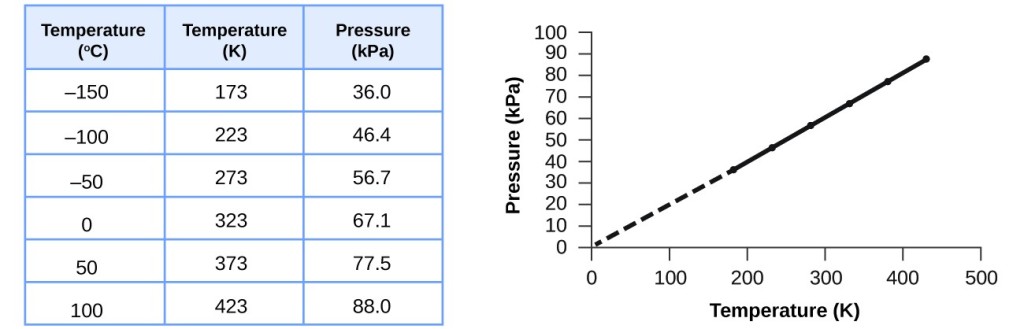
Figur 3. For et konstant volumen og en konstant mængde luft er tryk og temperatur direkte proportionale, forudsat at temperaturen er i kelvin. (Der kan ikke foretages målinger ved lavere temperaturer på grund af kondensering af gassen). Når denne linje ekstrapoleres til lavere tryk, når den et tryk på 0 ved -273 °C, hvilket er 0 på kelvinskalaen og den lavest mulige temperatur, kaldet det absolutte nulpunkt.

Guillaume Amontons var den første til empirisk at fastslå forholdet mellem trykket og temperaturen for en gas (~1700), og Joseph Louis Gay-Lussac bestemte forholdet mere præcist (~1800). På grund af dette er P-T-forholdet for gasser kendt som enten Gay-Lussacs lov eller Amontons’ lov. Under begge navne siger den, at trykket i en given mængde gas er direkte proportionalt med dens temperatur på kelvinskalaen, når volumenet holdes konstant. Matematisk kan dette skrives:

\large P\propto T

\large P=\text{konstant}\times T

\large P=k\times T

hvor ∝ betyder “er proportional med”, og k er en proportionalitetskonstant, der afhænger af gassens identitet, mængde og volumen.

\large\frac{{P}_{1}}}{{T}_{1}}}=\frac{{{P}_{2}}}{{T}_{2}}}

Denne ligning er nyttig til tryk-temperatur-beregninger for en indesluttet gas ved konstant volumen. Bemærk, at temperaturerne skal være på kelvinskalaen for alle gaslovsberegninger (0 på kelvinskalaen og den lavest mulige temperatur kaldes det absolutte nulpunkt). (Bemærk også, at der er mindst tre måder, hvorpå vi kan beskrive, hvordan trykket i en gas ændrer sig, når dens temperatur ændrer sig.) Vi kan bruge en tabel med værdier, en graf eller en matematisk ligning.)

Volumen og temperatur: Charles’ lov

Hvis vi fylder en ballon med luft og forsegler den, indeholder ballonen en bestemt mængde luft ved atmosfærisk tryk, lad os sige 1 atm. Hvis vi lægger ballonen i et køleskab, bliver gassen indeni kold, og ballonen krymper (selv om både mængden af gas og dens tryk forbliver konstant). Hvis vi gør ballonen meget kold, vil den krympe meget, og den udvider sig igen, når den bliver varmet op.

Disse eksempler på temperaturens virkning på volumenet af en given mængde af en indesluttet gas ved konstant tryk er generelt sande: Volumenet øges, når temperaturen stiger, og mindskes, når temperaturen falder. Volumen-temperatur-data for en 1 mol prøve af metangas ved 1 atm er anført og grafisk vist i figur 4.

Figur 4. Volumen og temperatur er lineært sammenhængende for 1 mol metangas ved et konstant tryk på 1 atm. Hvis temperaturen er i kelvin, er volumen og temperatur direkte proportionale. Linjen stopper ved 111 K, fordi metan bliver flydende ved denne temperatur; når den ekstrapoleres, skærer den grafernes oprindelse, hvilket repræsenterer en temperatur på det absolutte nulpunkt.

Sammenhængen mellem volumen og temperatur for en given mængde gas ved konstant tryk er kendt som Charles’ lov som en anerkendelse af den franske videnskabsmand og ballonflyvningspioner Jacques Alexandre César Charles. Charles’ lov fastslår, at volumenet af en given gasmængde er direkte proportional med dens temperatur på kelvinskalaen, når trykket holdes konstant.

Matematisk kan dette skrives som:

\large V\propto T

\large V=\text{konstant}\cdot T

\large V=k\cdot T

med k som en proportionalitetskonstant, der afhænger af mængden af og trykket i gassen.

\large\frac{{V}_{1}}}{{T}_{1}}}=\frac{{V}_{2}}}{{T}_{2}}}

Volume og tryk: Boyles lov

Hvis vi delvist fylder en lufttæt sprøjte med luft, indeholder sprøjten en bestemt mængde luft ved konstant temperatur, f.eks. 25 °C. Hvis vi langsomt skubber stemplet ind, mens temperaturen holdes konstant, komprimeres gassen i sprøjten til et mindre volumen, og trykket stiger; hvis vi trækker stemplet ud, øges volumenet, og trykket falder. Dette eksempel på virkningen af volumen på trykket i en given mængde af en indesluttet gas gælder generelt. Hvis man mindsker volumenet af en indesluttet gas, vil trykket stige, og hvis man øger volumenet, vil trykket falde. Hvis volumenet øges med en vis faktor, falder trykket faktisk med samme faktor og omvendt. Volumen-tryksdata for en luftprøve ved stuetemperatur er vist grafisk i figur 5.

Figur 5. Når en gas optager et mindre volumen, udøver den et højere tryk; når den optager et større volumen, udøver den et lavere tryk (under forudsætning af, at gasmængden og temperaturen ikke ændres). Da P og V er omvendt proportionale, er en graf med 1/P vs. V lineær.

I modsætning til P-T- og V-T-forholdet er tryk og volumen ikke direkte proportionale med hinanden. I stedet udviser P og V omvendt proportionalitet: En forøgelse af trykket resulterer i et fald i gassens volumen. Matematisk kan dette skrives:

\stort P\propto 1\text{/}V\text{ eller }P=k\cdot 1\text{/}V\text{ eller }P\cdot V=k\text{ eller }{P}_{1}{V}_{1}={P}_{2}{V}_{2}

med k som en konstant. Grafisk vises denne sammenhæng ved den rette linje, der fremkommer ved at plotte den inverse af trykket \large\left(\frac{1}{P}\right) mod volumen (V), eller den inverse af volumen \large\left(\frac{1}{V}\right) mod trykket (V). Grafer med krumme linjer er vanskelige at aflæse nøjagtigt ved lave eller høje værdier af variablerne, og de er vanskeligere at anvende til at tilpasse teoretiske ligninger og parametre til eksperimentelle data. Af disse grunde forsøger forskere ofte at finde en måde at “linearisere” deres data på. Hvis vi plotter P mod V, får vi en hyperbel (se figur 6).

Sammenhængen mellem volumen og tryk for en given gasmængde ved konstant temperatur blev første gang offentliggjort af den engelske naturfilosof Robert Boyle for over 300 år siden. Det er sammenfattet i det udsagn, der i dag er kendt som Boyles lov: Rumfanget af en given gasmængde ved konstant temperatur er omvendt proportional med det tryk, som den måles under.

Kemi i praksis: Åndedræt og Boyles lov

Hvad gør du ca. 20 gange i minuttet i hele dit liv, uden pause og ofte uden at være klar over det? Svaret er naturligvis åndedræt, eller vejrtrækning. Hvordan fungerer det? Det viser sig, at gaslovene gælder her. Dine lunger optager den gas, som din krop har brug for (ilt), og skiller sig af med affaldsgas (kuldioxid). Lungerne er lavet af svampet, elastisk væv, der udvider sig og trækker sig sammen, mens du trækker vejret. Når du indånder, trækker dit mellemgulv og dine interkostalmuskler (musklerne mellem ribbenene) sig sammen, hvilket udvider brysthulen og gør dit lungevolumen større. Stigningen i volumen fører til et fald i trykket (Boyles lov). Dette får luften til at strømme ind i lungerne (fra højt tryk til lavt tryk). Når du udånder, vender processen om: Dit mellemgulv og dine ribbenmuskler slapper af, din brysthule trækker sig sammen, og dit lungevolumen mindskes, hvilket får trykket til at stige (Boyle’s lov igen), og luften strømmer ud af lungerne (fra højt tryk til lavt tryk). Derefter trækker du vejret ind og ud igen og igen og gentager denne cyklus efter Boyle’s lov resten af livet (figur 7).

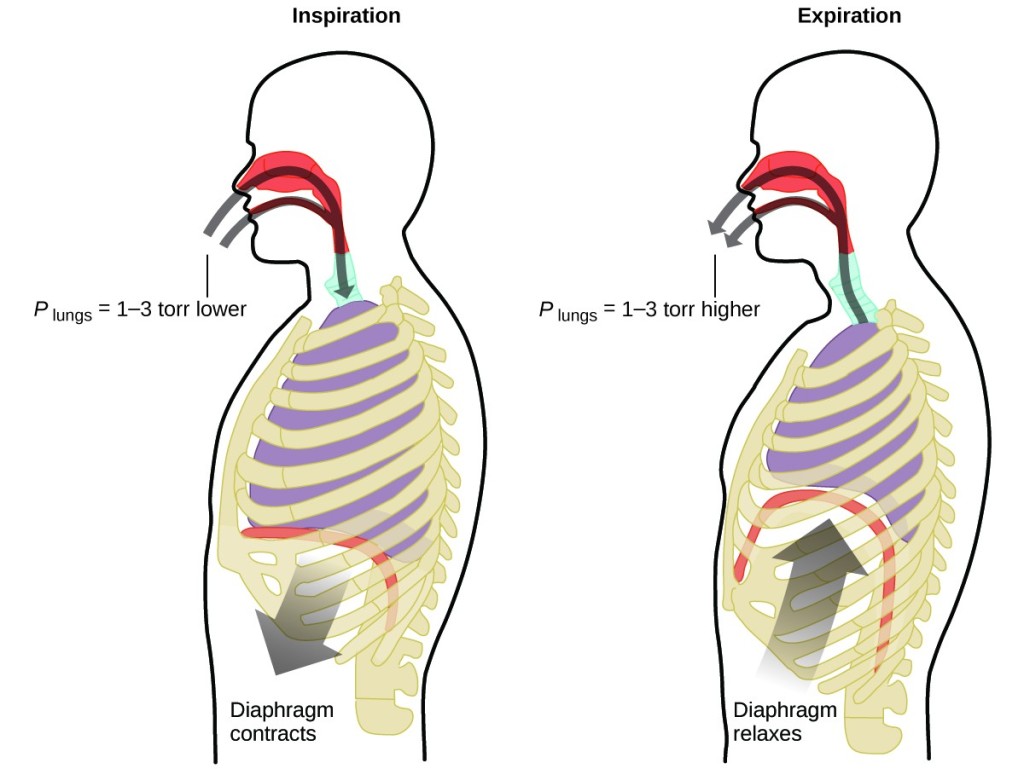
Figur 7. Åndedrættet opstår, fordi ekspanderende og kontraherende lungevolumen skaber små trykforskelle mellem dine lunger og dine omgivelser, hvilket får luft til at blive trukket ind i og presset ud af dine lunger.

Mol gas og volumen: Avogadros lov

Den italienske videnskabsmand Amedeo Avogadro fremsatte i 1811 en hypotese for at forklare gassers opførsel, som fastslog, at lige store mængder af alle gasser, målt under de samme temperatur- og trykforhold, indeholder det samme antal molekyler. Med tiden blev denne sammenhæng understøttet af mange eksperimentelle observationer, som udtrykt ved Avogadros lov: For en indesluttet gas er volumen (V) og antal mol (n) direkte proportionale, hvis både tryk og temperatur forbliver konstante.

I ligningsform skrives dette som:

\large\begin{array}{ccccc}V\propto n& \text{or}& V=k\times n& \text{or}& \frac{{V}_{1}}}{{n}_{1}}}=\frac{{V}_{2}}}{{n}_{2}}}\end{array}

Matematiske sammenhænge kan også bestemmes for de andre variabelpar, såsom P versus n, og n versus T.

Glossar

absolut nulpunkt: temperatur, ved hvilken en gas’ volumen ville være nul i henhold til Charles’ lov.

Avogadros lov: volumen af en gas ved konstant temperatur og tryk er proportional med antallet af gasmolekyler

Boyles lov: volumen af et givet antal mol gas holdt ved konstant temperatur er omvendt proportional med det tryk, under hvilket det måles

Charles’ lov:

Gay-Lussacs lov: Volumen af et givet antal mol gas er direkte proportional med dens kelvin-temperatur, når trykket holdes konstant

Gay-Lussacs lov: (også Amontons lov): Trykket for et givet antal mol af en gas er direkte proportionalt med dens kelvin-temperatur, når volumen holdes konstant