Hvad kan man bruge tegnetabeller til?
Et godt spørgsmål er nu: Hvad er pointen med at lære om tegnetabeller? Det enkle svar er, at symmetrien og den tilhørende karaktertabel for et molekyle kan bruges til at fortolke og forudsige mange aspekter af kemisk betydningsfulde spektroskopier såvel som bindinger. Vi vil illustrere dette næste gang ved at fokusere på et molekyls vibrationsformer.
I laboratoriet kan vi indsamle nyttige eksperimentelle data ved hjælp af infrarød (IR) og Raman-spektroskopi. Disse data kan sammenlignes med antallet af IR- og/eller Raman-aktive bånd, som forudsiges ved anvendelse af gruppeteori og den korrekte karaktertabel. Matematikken (gruppeteori og matrixalgebra) bag denne behandling tjener som et solidt teoretisk grundlag. De nedenfor beskrevne manipulationer fungerer, fordi alle symmetrioperationer i et molekyle udgør en matematisk gruppe og adlyder gruppens regler. Som tidligere nævnt behøver vi ikke at beherske dette område af matematikken for at kunne gøre god brug af karaktertabeller.
Frihedsgrader og vibrationer i molekyler
Her vil vi indledningsvis diskutere frihedsgraderne for et simpelt molekyle (vand). Vi vil meget hurtigt se, hvorfor det er meget fordelagtigt at anvende symmetri, når vi undersøger større molekyler.
For et molekyle med “N” atomer er der 3N frihedsgrader (husk, at vi lever i en 3-dimensionel verden med x, y, z-koordinater). For et ikke-lineært molekyle kan 3 frihedsgrader underskrives til translokationer – bevægelse af et legeme som helhed (Tx, Ty, Tz) og 3 til rotationer (Rx, Ry, Rz). De resterende bevægelser af atomerne er forskydninger af atomerne fra deres middelpositioner – tyngdepunktet ændres ikke. Disse grundlæggende vibrationer betegnes som “normale tilstande”. Et ikke-lineært molekyle har således 3N-6 normale tilstande. For vand er antallet af normale tilstande 3 (3 x 3 – 6 = 3). For lineære molekyler er der 3N-5 normalmodes.
For vand, som naturligvis er blevet studeret intensivt, ved vi, at de 3 vibrationer er som følger:
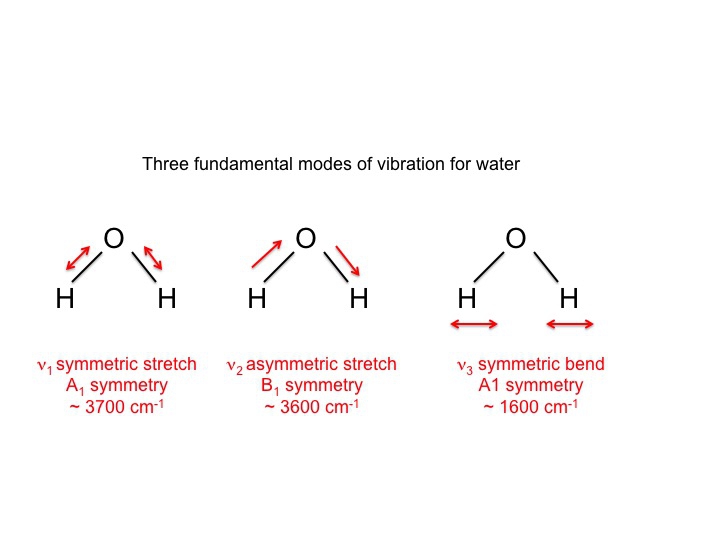
De symboler, der bruges til at beskrive disse modes (A1, B1), er de samme Mulliken-symboler, som vi stødte på i vores diskussion af karaktertabeller. Med andre ord kan vibrationerne, som er molekylære egenskaber, beskrives ved hjælp af symmetriarter eller irreducible repræsentationer. Faktisk bruger en stor del af den litteratur, der omhandler vibrationsspektroskopi, disse symboler som en kortfattet måde at kommunikere information på.
Det burde være ret indlysende, at antallet af vibrationer stiger hurtigt ved selv beskedne stigninger i antallet af atomer i molekylet. Det bliver nu meget vanskeligere at bestemme vibrationernes art ved inspektion (som vi gjorde for vand). For eksempel kan man overveje følgende forbindelser:
H2O 3 atomer 3 vibrationer
PH3 4 atomer 6 vibrationer
CO22- 4 atomer 6 vibrationer
XeF4 5 atomer 9 vibrationer
B2H6 8 atomer 18 vibrationer
For diboran (B2H6), som har D2h-symmetri, ville det være en uoverkommelig opgave at finde ud af arten og symmetriarterne af alle 18 vibrationer ved inspektion. Bevæbnet med karaktertabellen for D2h og viden om symmetriegenskaber er det imidlertid en ligetil opgave at bestemme symmetriarten for alle vibrationer.
For vands vedkommende kunne vi præsentere karaktertabellen (C2v) med de 3 vibrationer (ν1, v2, v3) opført i kolonnen med molekylære egenskaber som vist nedenfor. (ν = græsk symbol “nu”)

Men generelt er denne fremgangsmåde dog upraktisk. Tag f.eks. pyridin (C5H5N). Punktgruppen er også C2v, men molekylet har 11 atomer. Antallet af fundamentale vibrationsformer er 27 ( 3 x 11 – 6 = 27).
I dette tilfælde ville vi være nødt til at opstille en C2v-karaktertabel, der viser symmetrierne for alle 27 vibrationer. Af denne grund er vibrationer normalt ikke medtaget i karaktertabeller. I stedet er det op til brugeren (dig) at bestemme antallet og typen af vibrationer (som defineret af deres symmetriarter) for alle molekyler, som man støder på. Hvordan vi gør dette, er beskrevet nedenfor.
Reducible repræsentationer
Som tidligere nævnt er en af de vigtige egenskaber ved karaktertabeller, at symmetrioperationerne er medlemmer af en matematisk gruppe, og at der findes vigtige relationer mellem dem. Generelt kan det samme siges om symmetriarter eller irreducible repræsentationer af de molekylære egenskaber. De produkter, der fremkommer ved at kombinere karaktererne af irreducible repræsentationer enten ved multiplikation eller addition/subtraktion, adlyder også gruppens regler. De nye repræsentationer er ikke længere de mest enkle mulige og kaldes “reducerbare repræsentationer”, fordi de kan “reduceres” ned til deres bestanddele.
For eksempel kan for vand symmetrierne for translationer (Tx, Ty, Tz) uddrages direkte fra C2v-karaktertabellen. De er A1, B1 og B2. Vi kan repræsentere alle disse tre frihedsgrader ved en repræsentation ΓT, og vi kan skrive nedenstående udtryk. (Γ = det store græske bogstav “gamma”).
ΓT = A1 + B1 + B2
Vi ved, at A1, B1 og B2 blot er forkortede betegnelser for symmetriarterne (irreducible repræsentationer). Vi kan derfor blot nedskrive tegnene for ΓT ved at lægge de enkelte tegn for A1, B1 og B2 fra C2v-tegntabellen sammen.
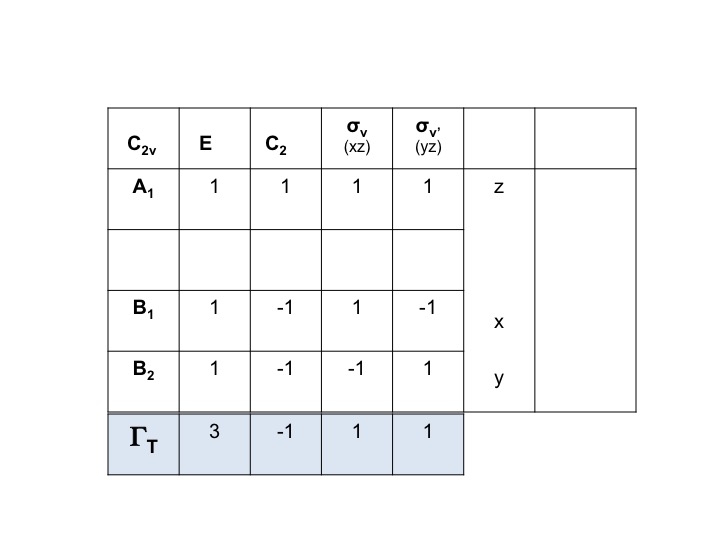
Dermed er ΓT = 3 -1 1 1 1.
Dette er en gyldig reducerbar repræsentation og et medlem af C2v-gruppen.
På samme måde kan vi nedskrive den reducerbare repræsentation for alle tre rotationer og alle vibrationer.
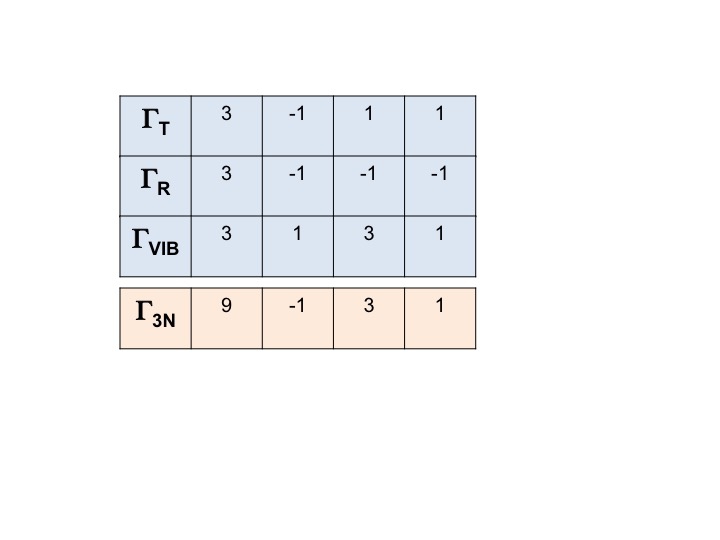
Den repræsentation for ALLE frihedsgrader for molekylet (3N) kan skrives som
Γ3N = ΓT + ΓR + ΓVIB
og den reducerbare repræsentation for den fås ved simpelthen at summere tegnene for ΓT, ΓR og ΓVIB.
Γ3N = 9 -1 3 1
Gem dette til efterretning – det kommer op senere!
Og selv om tegnsættet 9 -1 3 1 er et gyldigt medlem af C2v-gruppen er det ikke særlig nyttigt, når man diskuterer molekylære egenskaber. Det, der virkelig er brug for, er sproget for de kortfattede symmetriarter (Mulliken-symboler, A1, B1 osv.). Med andre ord ønsker vi at udtrykke Γ3N i form af A1, B1 osv. Ud fra de oplysninger, der er behandlet ovenfor, kan det let vises ved inspektion, at:
Γ3N = 3A1 +A2 + 3B1 +2B2
Den gode nyhed er, at vi for andre mere komplekse molekyler ikke behøver at udføre denne opgave ved inspektion, fordi:
1. Vi kan nemt generere Γ3N som en reducerbar repræsentation for et molekyle (hvis vi kender dets punktgruppesymmetri).
2. Vi kan nemt omdanne den reducerbare repræsentation Γ3N til summen af dets symmetriarter (Mulliken-symboler) ved hjælp af en “simpel” formel, der kaldes reduktionsformlen.
Generel metode til at opnå Γ3N
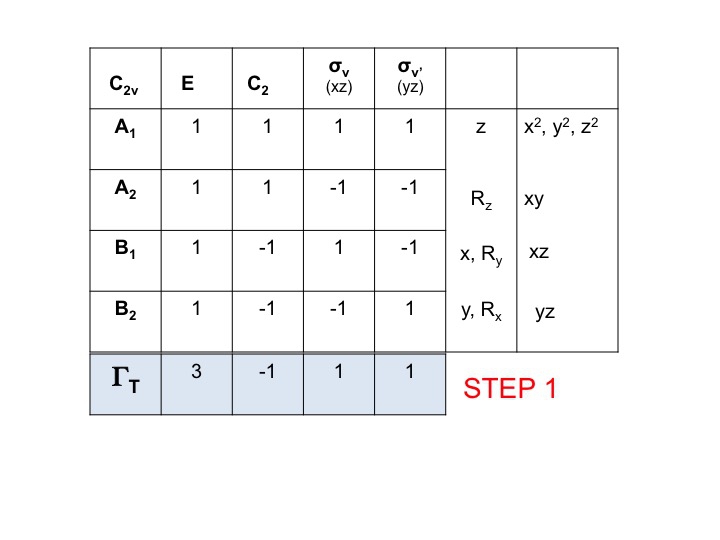
Stræk 1
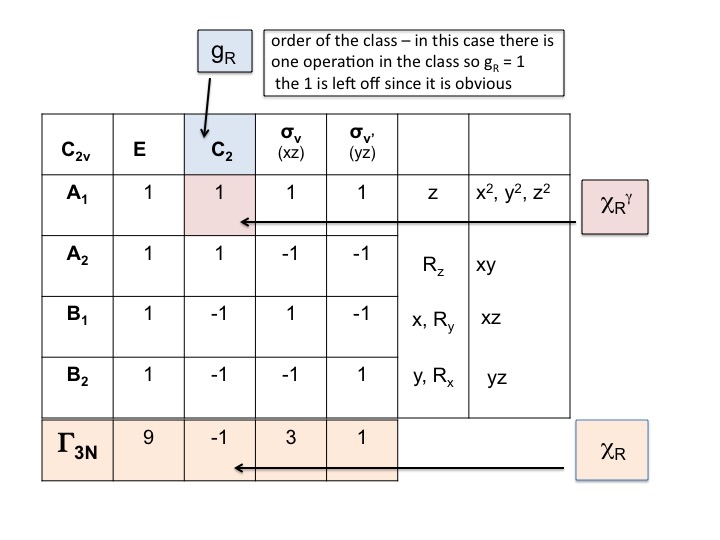
Tag karaktertabellen for molekylet og tilføj en række i bunden. I denne række genererer du den reducerbare repræsentation for ΓT (eller Γxyz) som vi gjorde ovenfor, blot ved at tilføje de tegn for hver operation, der svarer til molekyleegenskaberne for x, y og z. For C2v har vi allerede vist, at det er de tegn, der svarer til A1, B1 og B2.
Stræk 2
Føj endnu en række under ΓT og skriv antallet af atomer, der IKKE FORANDRER deres placering under hver symmetrioperation, op. Det er her, du indser, hvor nyttigt et rigtigt molekylærmodelsæt er. For at gøre dette skal du også vide, hvor symmetrielementerne befinder sig, og hvordan symmetrioperationerne påvirker molekylet. Selvfølgelig ved du allerede, hvordan du skal gøre dette, fordi du har studeret Schönflies notation og ved, hvordan man tildeler punktgruppen for et molekyle. Karaktertabellen har også alle symmetrioperationer opført efter klasse langs den øverste række.
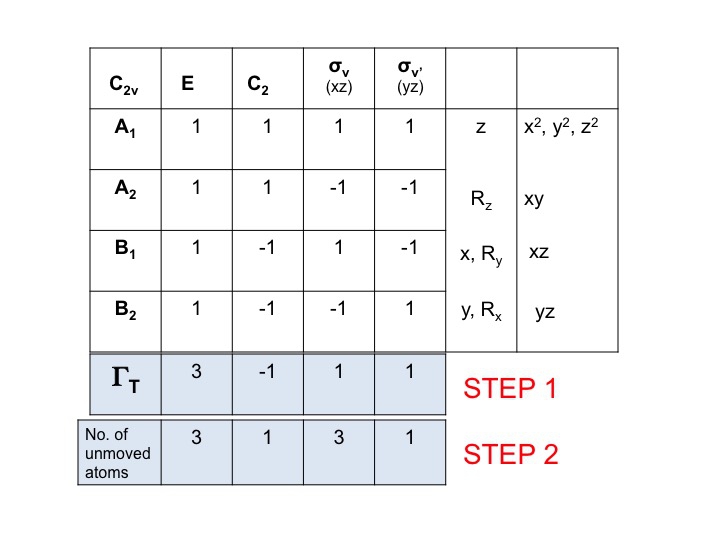
Så for vand (3 atomer) under E er der 3 ubevægelige atomer, men for C2 bevæger begge H’er sig, men da O-atomet sidder på C2-aksen ændrer det ikke sin placering, og derfor noterer vi 1 under C2-kolonnen. Det nye sæt tal, der blev genereret i trin 2 (3 1 3 3 1), er også en reducerbar repræsentation i C2v og adlyder gruppens regler.
Strin 3
I dette trin multiplicerer vi simpelthen de tegn, der er blevet genereret i trin 1 og 2, sammen. Resultatet (tredje række) er den reducerbare repræsentation for Γ3N (eller ΓTOT). Så enkelt er det.
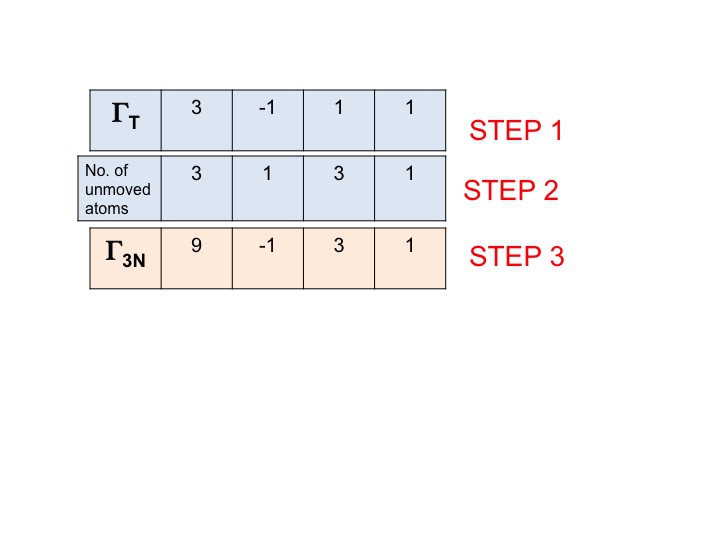
Du vil bemærke, at den nye reducerbare repræsentation (9 -1 1 3) er identisk med den repræsentation for Γ3N, som vi tidligere har fået ved inspektion.
Reduktion af den reducerbare repræsentation
For at omdanne EN reducerbar repræsentation til summen af dens irreducerbare repræsentationer (symmetriarter eller Mulliken-symboler) bruger vi en reduktionsformel:

Disse oplysninger kan du nemt finde i karaktertabellen:
Vi vender tilbage til vores eksempel for vand: Punktgruppe C2v, orden (g) = 4
Den reducerbare repræsentation for Γ3N = 9 -1 3 1
Det antal gange A1 optræder i denne repræsentation er derfor
aA1 = 1/4 { 1.1.1.9 + 1.1.1. (-1) + 1.1.3 +1.1.1} = 3
så Γ3N indeholder 3 A1-symmetriske arter. Antallet af de øvrige symmetriarter beregnes som følger:
aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).3 + 1.(-1).1 } = 1 en A2 tilstede
aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 3 B1 stede
aB2 = 1/4 {1.1.9 + 1.(-1)(-1)(-1) + 1.(-1).3 + 1.1.1.1} = 2 2 2 B2 tilstede
Vi kan nu skrive Γ3N = 3A1 + A2 + 3B1 + 2B2 (præcis hvad vi fik ved “inspektion” ovenfor. Vi kan nu trække symmetriarterne for translationer og rotationer fra, og dette vil give os antallet og symmetriarterne for de fundamentale vibrationsformer. ΓT og ΓR kan fås direkte fra karaktertabellen.
Γ3N = 3A1 + A2 + 3B1 + 2B2
ΓT = A1 + B1 + B2
ΓR = A2 + B1 + B2
ΓVIB = Γ3N – ΓT – ΓR = 2A1 +B1
Så de tre normale vibrationsformer for vand har symmetrierne A1, A1 og B1.
Vi har nu en generel metode til at bestemme alle de fundamentale vibrationsformer for et molekyle og til at udtrykke disse former i Mulliken-symbolernes kortfattede sprog. Dette er en af de opgaver, som du vil blive testet på i eksamen 1. Den bedste måde at blive fortrolig med denne metode på er at øve sig på så mange mulige eksempler som muligt!
Næste: Udvælgelsesregler