Jednou z rostoucích oblastí zájmu vědců zkoumajících význam, moc nebo vliv mezi entitami je tzv. teorie grafů. Kořeny teorie grafů sahají do roku 1736, kdy matematik Carl Ehler seznámil Leonharda Eulera s problémem mostů v Konigsbergu.
Problém mostů v Konigsbergu vychází z bývalého německého města Konigsberg, které leží na obou březích řeky Pregel. V jeho středu se nacházely dva velké ostrovy, které byly navzájem a s břehy řeky spojeny sedmi mosty. Carl Ehler se stal posedlým hledáním trasy, kterou by prošel přes každý ze sedmi mostů, aniž by přes některý z nich přešel více než jednou. Ehler se obrátil na švýcarského matematika Leonharda Eulera. Euler potvrdil Ehlerovu hypotézu, že problém nemá řešení, a Eulerovo vysvětlení bylo podkladem pro nové matematické paradigma nazvané Geometrie polohy.
Eulerovo nové geometrické paradigma tvrdilo, že na poloze mostů nezáleží. Problém lze naopak zjednodušit tím, že každý most proměníme v bod (uzel) s přímkami (hranami), které představují vazby mezi nimi. Tento postup používání uzlů a hran je dnes znám jako teorie grafů.
Další informace o problému mostů v Königsbergu si můžete přečíst zde.
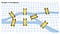
Zpočátku teorie grafů neměla při řešení problémů velký význam a matematici si jí příliš nevážili. Moderní výpočetní výkon pro zpracování velkých permutací však učinil principy Teorie grafů praktičtějšími. Tento článek vás naučí aplikovat principy Teorie grafů na analýzu v jazyce Python.


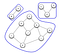
Ne všechny sítě v systému Graph jsou vzájemně propojeny. K tomuto nepropojení dochází při tvorbě komponent. Jak ukazuje následující graf, komponenta vzniká pouze tehdy, když má každý uzel cestu k jiným uzlům.
Aplikovaná teorie grafů v Pythonu
V Pythonu se často používá networkx pro aplikovanou teorii grafů známou také jako analýza sítí . Balík má užitečné funkce pro rychlé shrnutí charakteristik grafu. Můžete si prohlédnout níže uvedené kroky a sledovat, jak vytvoříme graf a pochopíme jeho složení.
Nejprve níže uvedený kód vytvoří prázdný objekt grafu P. V dalších krocích přidáme uzly a popíšeme hrany.
Argumenty jako <object>.nodes() nebo <object>.edges() slouží k rychlému zobrazení všech uzlů a hran systému grafů.
print(P.nodes())print(P.edges())
Nakonec se k vizualizaci sítě použije nx.draw.
%matplotlib inline
import matplotlib.pyplot as plt
nx.draw(P, with_labels = True)
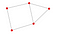
Cvičení 1:
Teď, když jsou probrány základní pojmy grafů, jsou následující cvičení vhodnou metodou k procvičení:
- Kolik uzlů má výše uvedený graf?
- Kolik hran je ve výše uvedeném grafu?
- Jaká je geodézie pro E a C?
- Je v grafu více než 1 komponenta?
Použití reálných dat
Následující cvičení použije data o letech v rámci Spojených států v roce 2015. Soubor dat obsahuje kromě atributů, které popisují let, včetně doby letu a zpoždění (v souvislosti s počasím, bezpečností nebo leteckou společností), také výchozí a cílová letiště.
Protože je soubor dat rozsáhlý, cvičení se zaměří na lety vycházející z letišť v oblasti Los Angeles (Los Angeles (LAX), Burbank (BUR), Orange County (SNA) a San Bernardino County (ONT)). Kromě toho se zaměříme na přezkoumání letů, které se podobají mému cestovnímu plánu společnosti Deloitte – odlétají v neděli a vracejí se ve čtvrtek.
Protože již máme údaje o původu a cíli, budou pole **** ORIGIN_AIRPORT a DESTINATION_AIRPORT sloužit jako zdrojová pole pro uzly a hrany – není třeba vytvářet uzly nebo hrany, jak jsme to udělali v prvním cvičení. Jakmile jsou uzly definovány, <object>.edges() poskytne všechny párové vztahy mezi nimi. Nakonec nx.draw pomůže vytvořit graf k hranám.

FG.edges()

nx.draw(FG, with_labels = True)

Výše uvedený výstup, jsou uzly označeny kódy letišť. Všechny hrany vedou na jedno ze čtyř letišť v oblasti Los Angeles, protože tato čtyři letiště byla jako jediná vybrána pro toto cvičení. Mezinárodní letiště Los Angeles (LAX) je největší z těchto čtyř letišť a z grafu je jasně patrné, že mnoho měst je dostupných pouze pro letiště LAX a ne z jiných menších letišť. To ukazuje na propojenost neboli centralitu stupně letiště LAX. V programu networkx se nx.algorithms.degree_centrality(<object>) ****používá ke zjištění centrality každého uzlu v systému grafů.
# Calculating the centrality of each of the airports
nx.algorithms.degree_centrality(FG)
Můžeme jít více do hloubky a použít krátkou „for smyčku“ k vytvoření hran mezi dvěma oblastmi zájmu. Například následující kód slouží k nalezení všech možných letů z okresu San Bernardino (ONT) do Newarku (EWR) v neděli nebo ve čtvrtek.
Z několika možností letu mezi okresem San Bernardino a Newarkem lze pomocí nx.dijkstra_path najít euklidovskou cestu (neboli nejkratší cestu).
#Finding the dijkstra path
djk_path = nx.dijkstra_path(FG, source='ONT', target='EWR')
djk_path
Cvičení 2:
- Vytvořte následující graf pomocí
nx.draw(). Poznámka: vaše síť nemusí vypadat přesně stejně, ale cesty, hrany a uzly by měly odpovídat níže uvedené síti. - Vytiskněte všechny hrany.
- Jaká je nejkratší cesta z L do F?

.