Less…
Pythagorova trojice je trojice kladných celých čísel 
, 
a 
taková, že existuje pravoúhlý trojúhelník s rameny 
a přeponou 
. Podle Pythagorovy věty to odpovídá nalezení kladných celých čísel 
, 
a 
splňujících
 |
(1)
|
Nejmenší a nejznámější Pythagorova trojice je 
. Pravoúhlý trojúhelník, který má tyto délky stran, se někdy nazývá trojúhelník 3,4,5.
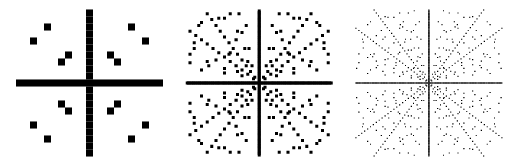
Výkresy bodů v 
rovině takové, že 
je Pythagorova trojice, jsou uvedeny výše pro postupně větší meze. Tyto grafy obsahují záporné hodnoty 
a 
, a jsou tedy symetrické kolem osy x i y.
Podobně jsou výše zobrazeny grafy bodů v rovině 
takové, že 
je Pythagorova trojice pro postupně větší meze.
Obvykle se uvažují pouze primitivní pythagorejské trojice (nazývané též „redukované“), v nichž 
a 
jsou relativně prvočíselné, protože z primitivních řešení lze triviálně generovat další. Primitivní trojice jsou znázorněny výše a hned je vidět, že radiální čáry odpovídající imprimitivním trojicím v původním grafu na tomto obrázku chybí. U primitivních řešení musí být jedno z 
nebo 
sudé a druhé liché (Shanks 1993, s. 141), přičemž 
je vždy liché.
Kromě toho je jedna strana každé pythagorovské trojice dělitelná 3, další 4 a další 5. Jedna strana může mít dva z těchto dělitelů, jako v (8, 15, 17), (7, 24, 25) a (20, 21, 29), nebo dokonce všechny tři, jako v (11, 60, 61).
Podle primitivní trojice 
získáme tři nové primitivní trojice z
 |
 |
 |
(2)
|
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
kde
 |
 |
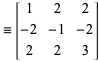(5)
|
 |
 |
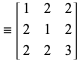(6)
|
 |
 |
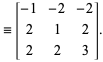(7)
|
Hall (1970) a Roberts (1977) dokazují, že 
je primitivní pythagorovská trojice, jestliže
 |
(8)
|
kde 
je konečný součin matic 
, 
, 
. Z toho vyplývá, že každá primitivní Pythagorova trojice musí být členem nekonečné matice
 |
(9)
|
Pythagoras a Babyloňané uvedli vzorec pro generování (ne nutně primitivních) trojic jako
 |
(10)
|
pro 
, který generuje množinu různých trojic neobsahujících ani všechny primitivní, ani všechny imprimitivní trojice (a kde ve speciálním případě 
, 
).
Raní Řekové uváděli
 |
(11)
|
kde 
a 
jsou relativně prvočíselné a opačné parity (Shanks 1993, str. 141), což generuje množinu různých trojic, která obsahuje právě prvočísla (po vhodném seřazení 
a 
).
Nechť 
je Fibonacciho číslo. Pak
 |
(12)
|
generuje různé pythagorejské trojice (Dujella 1995), i když ne vyčerpávajícím způsobem pro primitivní ani imprimitivní trojice. Obecněji řečeno, počínaje kladnými celými čísly 
, 
a konstrukcí Fibonacciho posloupnosti 
s členy 
, 
, 
, 
, 
, … generuje různé pythagorovské trojice
 |
(13)
|
(Horadam 1961), kde
 |
(24)
|
(Beiler 1966, str. 116). Všimněte si, že 
iff 
je prvočíslo nebo dvojnásobek prvočísla. Prvních několik čísel pro 
, 2, … je 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 4, 1, …. (OEIS A046079).
K nalezení počtu způsobů 
, kterými může být číslo 
přeponou primitivního pravoúhlého trojúhelníku, zapište jeho faktorizaci jako
 |
(25)
|
kde 
s má tvar 
a 
s má tvar 
. Počet možných primitivních pravoúhlých trojúhelníků je pak
 |
(26)
|
Např, 
, protože
 |
 |
 |
(27)
|
 |
 |
 |
(28)
|
H_p(n) pro 
, 2, … mají hodnoty 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, …. (OEIS A024362). Prvních několik prvočísel tvaru 
je 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, …. (OEIS A002144), takže nejmenší délky stran, které jsou přeponami 1, 2, 4, 8, 16, … primitivních pravoúhlých trojúhelníků, jsou 5, 65, 1105, 32045, 1185665, 48612265, …. (OEIS A006278).
Počet možných primitivních nebo neprimitivních pravoúhlých trojúhelníků, které mají 
jako přeponu, je
 |
 |
 |
(29)
|
 |
 |
 |
(30)
|
(oprava překlepu Beiler 1966, p. 117, kde se uvádí, že tento vzorec udává pouze počet neprimitivních řešení), kde 
je funkce součtu čtverců. Například existují čtyři různé celočíselné trojúhelníky s přeponou 65, protože
 |
(31)
|
Prvních několik čísel pro 
, 2, … je 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, …. (OEIS A046080). Nejmenší hypotenusy, které mají 
různých trojic, jsou 1, 5, 25, 125, 65, 3125, … (OEIS A006339). V následující tabulce jsou uvedeny hypotenusy, pro které existuje přesně 
různých pravoúhlých celočíselných trojúhelníků pro 
, 1, …, 5.
 |
OEIS | hypoteny, pro které existují  různé celočíselné trojúhelníky |
| 0 | A004144 | 1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, …. |
| 1 | A084645 | 5, 10, 13, 15, 17, 20, 26, 29, 30, 34, 35, … |
| 2 | A084646 | 25, 50, 75, 100, 150, 169, 175, 200, 225, …. |
| 3 | A084647 | 125, 250, 375, 500, 750, 875, 1000, 1125, 1375, … |
| 4 | A084648 | 65, 85, 130, 145, 170, 185, 195, 205, 221, 255, …. |
| 5 | A084649 | 3125, 6250, 9375, 12500, 18750, 21875, 25000, … |
Takže celkový počet způsobů, kterými může být 
buď ramenem, nebo přeponou pravoúhlého trojúhelníku, je dán vztahem
 |
(32)
|
Hodnoty pro 
, 2, … jsou 0, 0, 1, 1, 2, 1, 1, 2, 2, 2, 1, 4, 2, 1, 5, 3, …. (OEIS A046081). Nejmenší čísla 
, která mohou být stranami 
obecných pravoúhlých trojúhelníků pro 
, 2, …, jsou 3, 5, 16, 12, 15, 125, 24, 40, …. (OEIS A006593; Beiler 1966, s. 114).
Existuje 50 pythagorovských trojic s přeponou menší než 100, z nichž prvních několik, seřazených podle rostoucího 
, je (3, 4, 5), (6, 8,10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), … (OEIS A046083, A046084 a A009000).
Z těchto trojúhelníků je pouze 16 primitivních trojúhelníků s přeponou menší než 100 : (3, 4,5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65), (16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85), (39, 80, 89) a (65, 72, 97) (OEIS A046086, A046087 a A020882).
Počet trojic s přeponou 
označme 
, počet trojic s přeponou 
označme 
a počet primitivních trojic menších než 
označme 
. Následující tabulka pak shrnuje hodnoty pro mocniny 10.
 |
OEIS |  ,  , … |
 |
A101929 | 1, 50, 878, 12467, … |
 |
A101930 | 2, 52, 881, 12471, …. |
 |
A101931 | 1, 16, 158, 1593, … |
Lehmer (1900) dokázal, že počet primitivních řešení s hypotenózou menší než 
splňuje
 |
(33)
|
(OEIS A086201).
Inradia prvních několika primitivních pythagorejských trojúhelníků seřazených podle rostoucího 
jsou dána 1, 2, 3, 3, 6, 5, 4, 10, 5, …. (OEIS A014498).
Existuje obecná metoda pro získání trojic pythagorejských trojúhelníků se stejnými plochami. Vezměte tři množiny generátorů jako
 |
 |
 |
(34)
|
 |
 |
 |
(35)
|
 |
 |
 |
(36)
|
 |
 |
 |
(37)
|
 |
 |
 |
(38)
|
 |
 |
 |
(39)
|
Tedy pravoúhlý trojúhelník generovaný každou trojicí (
) má společný povrch
 |
(40)
|
(Beiler 1966, str. 126-127). Jediný extrém této funkce se vyskytuje v bodě 
. Protože 
pro 
, je nejmenší plocha sdílená třemi neprimitivními pravoúhlými trojúhelníky dána 
, což vede k ploše 840 a odpovídá trojicím (24, 70, 74), (40, 42, 58) a (15, 112, 113) (Beiler 1966, s. 126).
Mezi pravoúhlé trojúhelníky, jejichž plochu tvoří jediná číslice, patří 
(plocha 6) a 
(plocha 666666; Wells 1986, s. 89).
V roce 1643 vyzval Fermat Mersenna, aby našel pythagorejský trojúhelník, jehož přepona a součet ramen jsou čtverce. Fermat našel nejmenší takové řešení:
 |
 |
 |
(41)
|
 |
 |
 |
(42)
|
 |
 |
 |
(43)
|
s
 |
 |
 |
(44)
|
 |
 |
 |
(45)
|
Související úlohou je určit, zda zadané celé číslo 
může být plochou pravoúhlého trojúhelníku s racionálními stranami. 1, 2, 3 a 4 nejsou plochami žádného pravoúhlého trojúhelníku s racionálními stranami, ale 5 je (3/2, 20/3, 41/6), stejně jako 6 (3, 4, 5). Řešení úlohy zahrnuje eliptickou křivku
 |
(46)
|
Řešení (
, 
, 
) existuje, jestliže (46) má racionální řešení, v tom případě
 |
 |
 |
(47)
|
 |
 |
 |
(48)
|
(Koblitz 1993). Není známa žádná obecná metoda, jak určit, zda existuje řešení pro libovolné 
, ale technika navržená J. Tunnellem v roce 1983 umožňuje některé hodnoty vyloučit (Cipra 1996).
.