Více než 90 % přírodních a člověkem vyrobených pevných látek je krystalických. Většina pevných látek se tvoří s pravidelným uspořádáním svých částic, protože celkové přitažlivé interakce mezi částicemi jsou maximalizovány a celková mezimolekulární energie je minimalizována, když se částice nabalují co nejefektivněji. Pravidelné uspořádání na atomární úrovni se často odráží i na makroskopické úrovni. V tomto modulu prozkoumáme některé podrobnosti o strukturách kovových a iontových krystalických pevných látek a dozvíme se, jak se tyto struktury experimentálně určují.

Struktury kovů

Probírání krystalických pevných látek začneme úvahou o elementárních kovech, které jsou relativně jednoduché, protože každý z nich obsahuje pouze jeden typ atomu. Čistý kov je krystalická pevná látka s atomy kovu těsně vedle sebe v opakujícím se vzorci. Některé vlastnosti kovů obecně, jako je jejich kujnost a tažnost, jsou do značné míry způsobeny tím, že mají stejné atomy uspořádané v pravidelném vzoru. Rozdílné vlastnosti jednoho kovu ve srovnání s jiným částečně závisí na velikosti jejich atomů a na zvláštnostech jejich prostorového uspořádání. V následujících kapitolách se budeme zabývat podobnostmi a rozdíly čtyř nejběžnějších krystalových geometrií kovů.

Jednotkové buňky kovů

Strukturu krystalické pevné látky, ať už se jedná o kov nebo ne, nejlépe popíšeme, když vezmeme v úvahu její nejjednodušší opakující se jednotku, která se označuje jako jednotková buňka. Jednotková buňka se skládá z mřížkových bodů, které představují umístění atomů nebo iontů. Celá struktura se pak skládá z této jednotkové buňky opakující se ve třech rozměrech, jak je znázorněno na obrázku 1.

Obrázek 1. Jednotková buňka ukazuje umístění mřížkových bodů opakujících se ve všech směrech.

Začněme naše zkoumání struktury krystalové mřížky a jednotkových buněk nejjednodušší strukturou a nejzákladnější jednotkovou buňkou. Abychom si to představili, představme si, že vezmeme velké množství stejných kuliček, například tenisových míčků, a rovnoměrně je uspořádáme v nádobě. Nejjednodušší způsob, jak to udělat, by bylo vytvořit vrstvy, v nichž by koule v jedné vrstvě byly přímo nad koulemi ve vrstvě pod ní, jak je znázorněno na obrázku 2. Toto uspořádání se nazývá jednoduchá krychlová struktura a jednotková buňka se nazývá jednoduchá krychlová jednotková buňka nebo primitivní krychlová jednotková buňka.

Obrázek 2. Jsou-li atomy kovu uspořádány tak, že koule v jedné vrstvě jsou přímo nad nebo pod koulemi v jiné vrstvě, nazývá se mřížková struktura jednoduchá krychlová. Všimněte si, že koule jsou v kontaktu.

V jednoduché krychlové struktuře nejsou koule zabaleny tak těsně, jak by mohly být, a „vyplňují“ jen asi 52 % objemu nádoby. To je poměrně neefektivní uspořádání a v jednoduché krychlové struktuře krystalizuje pouze jeden kov (polonium, Po). Jak ukazuje obrázek 3, pevná látka s tímto typem uspořádání se skládá z rovin (nebo vrstev), v nichž se každý atom dotýká pouze čtyř nejbližších sousedů ve své vrstvě; jeden atom přímo nad ním ve vrstvě nad ním a jeden atom přímo pod ním ve vrstvě pod ním. Počet ostatních částic, se kterými se každá částice v krystalické pevné látce stýká, se nazývá její koordinační číslo. Pro atom polonia v jednoduchém krychlovém poli je tedy koordinační číslo šest.

Obrázek 3. Atom v jednoduché krychlové mřížkové struktuře se dotýká šesti dalších atomů, takže má koordinační číslo šest.

V jednoduché krychlové mřížce je jednotkovou buňkou, která se opakuje ve všech směrech, krychle vymezená středy osmi atomů, jak je znázorněno na obrázku 4. Na obrázku 4 je znázorněno koordinační číslo atomu. Atomy v sousedních rozích této jednotkové buňky se vzájemně dotýkají, takže délka hrany této buňky je rovna dvěma atomovým poloměrům neboli jednomu atomovému průměru. Krychlová jednotková buňka obsahuje pouze ty části těchto atomů, které se v ní nacházejí. Protože atom v rohu jednoduché kubické jednotkové buňky je obsažen celkem v osmi jednotkových buňkách, nachází se uvnitř konkrétní jednotkové buňky pouze jedna osmina tohoto atomu. A protože každá jednoduchá krychlová jednotková buňka má v každém ze svých osmi „rohů“ jeden atom, je v jedné jednoduché krychlové jednotkové buňce 8krát \frac{1}{8}=1 atom.

Obrázek 4. Vpravo je zobrazena krychlová jednotka, označená jako „8 rohů“. Jednoduchá krychlová mřížková jednotková buňka obsahuje v každém ze svých osmi rohů jednu osminu atomu, takže celkem obsahuje jeden atom.

Příklad 1: Výpočet atomového poloměru a hustoty pro kovy, část 1

Délka hrany jednotkové buňky alfa polonia je 336 pm.

1. Určete poloměr atomu polonia.
2. Určete hustotu alfa polonia.

Ukažte řešení

Alfa polonium krystalizuje v jednoduché krychlové jednotkové buňce:

1. Dva sousední atomy Po se vzájemně dotýkají, takže délka hrany této buňky je rovna dvěma poloměrům atomů Po: l=2r. Poloměr Po je tedy r=\dfrac{\text{l}}{2}=\dfrac{\text{336 pm}}{2}=\text{168 pm}.
2. Hustota je dána vztahem \text{hustota}=\dfrac{\text{hmota}}{\text{objem}}. Hustotu polonia lze zjistit stanovením hustoty jeho jednotkové buňky (hmotnost obsažená v jednotkové buňce dělená objemem jednotkové buňky). Protože jednotková buňka Po obsahuje jednu osminu atomu Po v každém ze svých osmi rohů, obsahuje jednotková buňka jeden atom Po.

Hmotnost jednotkové buňky Po lze zjistit takto:

\text{1 jednotková buňka Po}\krát \dfrac{\text{1 atom Po}}{\text{1 jednotková buňka Po}}\krát \dfrac{\text{1 mol Po}}{6.022\times {10}^{23}\text{Po atomy}}\times \dfrac{208,998\text{g}}{\text{1 mol Po}}=3.47\krát {10}^{-22}\text{g}

Objem jednotkové buňky Po lze zjistit takto:

V={l}^{3}={(336\krát {10}^{-10}\text{cm})}^{3}=3.79\krát {10}^{-23}{\text{cm}}^{3}

(Všimněte si, že délka hrany byla převedena z pm na cm, abychom získali obvyklé objemové jednotky pro hustotu)

Takže hustota \text{Po}=\dfrac{3.471\krát {10}^{-22}\text{g}}{3,79\krát {10}^{-23}{\text{cm}}^{3}}={\text{9,16 g/cm}}^{3}

Ověř si své znalosti

Délka hrany jednotkové buňky pro nikl je 0,3524 nm. Hustota Ni je 8,90 g/cm3. Krystalizuje nikl v jednoduché krychlové struktuře? Vysvětlete.

Ukažte řešení

Ne. Kdyby byl Ni jednoduchý krychlový, jeho hustota by byla dána:

\text{1 atom Ni}\times \dfrac{\text{1 mol Ni}}{6.022\times {10}^{23}\text{atomů Ni}}\times \dfrac{58,693\text{g}}{\text{1 mol Ni}}=9,746\times {10}^{-23}\text{g}
V={l}^{3}={(3,524\times {10}^{-8}\text{cm})}^{3}=4.376\krát {10}^{-23}{\text{cm}}^{3}

Tedy hustota Ni by byla =\dfrac{9,746\krát {10}^{-23}\text{g}}{4,376\krát {10}^{-23}{\text{cm}}^{3}}={\text{2.23 g/cm}}^{3}

Protože se skutečná hustota Ni této hodnotě neblíží, netvoří Ni jednoduchou krychlovou strukturu.

Většina krystalů kovů má jeden ze čtyř hlavních typů jednotkových buněk. Prozatím se zaměříme na tři kubické jednotkové buňky: jednoduchou kubickou (kterou jsme již viděli), tělesově centrovanou kubickou jednotkovou buňku a čelně centrovanou kubickou jednotkovou buňku – všechny jsou znázorněny na obrázku 5. (Všimněte si, že ve skutečnosti existuje sedm různých mřížkových soustav, z nichž některé mají více než jeden typ mřížky, celkem tedy 14 různých typů jednotkových buněk. Složitější geometrie si necháme na pozdější část tohoto modulu.“

Obrázek 5. Vpravo je stejný výkres se šesti červenými molekulami uvnitř políčka. Krychlové jednotkové buňky kovů ukazují (na horních obrázcích) umístění mřížkových bodů a (na dolních obrázcích) atomy kovu umístěné v jednotkové buňce.

Některé kovy krystalizují v uspořádání, které má krychlovou jednotkovou buňku s atomy ve všech rozích a atomem uprostřed, jak je znázorněno na obrázku 6. Na obrázku 6 je znázorněno uspořádání krychlové jednotkové buňky s atomy ve všech rozích. Takové těleso se nazývá těleso s centrovanou krychlí (BCC). Atomy v rozích jednotkové buňky BCC se vzájemně nedotýkají, ale dotýkají se atomu ve středu. Jednotková buňka BCC obsahuje dva atomy: jednu osminu atomu v každém z osmi rohů ( 8\krát \frac{1}{8}=1 atom z rohů) a jeden atom ze středu. Každý atom v této struktuře se dotýká čtyř atomů ve vrstvě nad ním a čtyř atomů ve vrstvě pod ním. Atom ve struktuře BCC má tedy koordinační číslo osm.

Obrázek 6. Vpravo vidíme, že se krychle rozpadá na dvě části. V tělesově centrované krychlové struktuře se atomy v určité vrstvě navzájem nedotýkají. Každý atom se dotýká čtyř atomů ve vrstvě nad ním a čtyř atomů ve vrstvě pod ním.

Atomy v uspořádání BCC jsou mnohem efektivněji zabaleny než v jednoduché krychlové struktuře, zabírají přibližně 68 % celkového objemu. Mezi izomorfní kovy s BCC strukturou patří K, Ba, Cr, Mo, W a Fe při pokojové teplotě. (O prvcích nebo sloučeninách, které krystalizují se stejnou strukturou, se říká, že jsou izomorfní.)

Mnoho dalších kovů, například hliník, měď a olovo, krystalizuje v uspořádání, které má krychlovou jednotkovou buňku s atomy ve všech rozích a ve středech každé stěny, jak je znázorněno na obrázku 7. Na obrázku 7 je znázorněno uspořádání krychlové jednotkové buňky s atomy ve všech rozích. Toto uspořádání se nazývá krychlové těleso s centrovaným povrchem (FCC). Jednotková buňka FCC obsahuje čtyři atomy: osminu atomu v každém z osmi rohů (8\krát \frac{1}{8}=1 atom z rohů) a polovinu atomu na každé ze šesti stěn (6\krát \frac{1}{2}=3 atomy ze stěn). Atomy v rozích se dotýkají atomů ve středech sousedních stěn podél úhlopříček stěn krychle. Protože atomy leží na shodných bodech mřížky, mají shodné prostředí.

Obrázek 7. Vpravo jsou šedé molekuly, které jsou vně krychle, oholeny, takže zůstaly jen části šedých molekul a šest polovin červených molekul (protože byly rozděleny na poloviny). Krychlové těleso s centrovanými stěnami má atomy v rozích a, jak název napovídá, ve středech stěn svých jednotkových buněk.

Atomy v uspořádání FCC jsou nabaleny co nejtěsněji u sebe, přičemž atomy zabírají 74 % objemu. Tato struktura se také nazývá kubické nejtěsnější balení (CCP). V CCP jsou tři opakující se vrstvy hexagonálně uspořádaných atomů. Každý atom se dotýká šesti atomů ve své vrstvě, tří ve vrstvě nad ní a tří ve vrstvě pod ní. V tomto uspořádání se každý atom dotýká 12 blízkých sousedů, a má tedy koordinační číslo 12. Skutečnost, že uspořádání FCC a CCP jsou ekvivalentní, nemusí být hned zřejmá, ale proč se vlastně jedná o stejnou strukturu, je znázorněno na obrázku 8.

Obrázek 8. Uspořádání CCP se skládá ze tří opakujících se vrstev (ABCABC…) hexagonálně uspořádaných atomů. Atomy ve struktuře CCP mají koordinační číslo 12, protože se dotýkají šesti atomů ve své vrstvě plus tří atomů ve vrstvě nad ní a tří atomů ve vrstvě pod ní. Pootočením perspektivy vidíme, že struktura CCP má jednotkovou buňku, jejíž stěna obsahuje atom z vrstvy A v jednom rohu, atomy z vrstvy B přes úhlopříčku (ve dvou rozích a uprostřed stěny) a atom z vrstvy C ve zbývajícím rohu. To je totéž jako krychlové uspořádání se soustředěnými stěnami.

Protože těsnější uspořádání maximalizuje celkovou přitažlivost mezi atomy a minimalizuje celkovou mezimolekulovou energii, atomy většiny kovů se balí tímto způsobem. V jednoduchých krystalických strukturách kovů nacházíme dva typy nejtěsnějšího balení: CCP, se kterým jsme se již setkali, a hexagonální nejtěsnější balení (HCP), které je znázorněno na obrázku 9. Oba se skládají z opakujících se vrstev hexagonálně uspořádaných atomů. V obou typech je druhá vrstva (B) umístěna na první vrstvě (A) tak, že každý atom ve druhé vrstvě je v kontaktu se třemi atomy v první vrstvě. Třetí vrstva je umístěna jedním ze dvou způsobů. V HCP jsou atomy ve třetí vrstvě přímo nad atomy v první vrstvě (tj. třetí vrstva je také typu A) a stohování se skládá ze střídajících se těsně zabalených vrstev typu A a typu B (tj. ABABAB⋯). V případě CCP nejsou atomy ve třetí vrstvě nad atomy v žádné z prvních dvou vrstev (tj. třetí vrstva je typu C) a uspořádání se skládá ze střídajících se těsně zabalených vrstev typu A, typu B a typu C (tj. ABCABCABC⋯). Přibližně dvě třetiny všech kovů krystalizují v nejtěsněji zabalených vrstvách s koordinačním číslem 12. Mezi kovy, které krystalizují ve struktuře HCP, patří Cd, Co, Li, Mg, Na a Zn a mezi kovy, které krystalizují ve struktuře CCP, patří Ag, Al, Ca, Cu, Ni, Pb a Pt.

Obrázek 9. V obou typech nejužšího balení jsou atomy zabaleny co nejkompaktněji. Šestihranné nejbližší balení se skládá ze dvou střídajících se vrstev (ABABAB…). Kubické nejtěsnější uspořádání se skládá ze tří střídajících se vrstev (ABCABCABC…).

Příklad 2: Výpočet atomového poloměru a hustoty pro kovy, část 2

Vápník krystalizuje v kubické struktuře s centrovaným povrchem. Délka hrany jeho jednotkové buňky je 558,8 pm.

1. Jaký je atomový poloměr Ca v této struktuře?
2. Vypočítejte hustotu Ca.

Zobrazit řešení

Část 1

Ve struktuře FCC se atomy Ca dotýkají napříč diagonálou stěny, takže délka diagonály je rovna čtyřem poloměrům atomů Ca (d = 4r). Dvě sousední hrany a úhlopříčka stěny tvoří pravoúhlý trojúhelník s délkou každé strany 558,8 pm a délkou přepony rovnou čtyřem atomovým poloměrům Ca:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}\longrightarrow {(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}={(4r)}^{2}

Solving this gives r=\sqrt{\dfrac{{(558.8\text{pm})}^{2}+{(558.5\text{pm})}^{2}}{16}}=\text{197,6 pmg pro poloměr Ca}.

Část 2

Hustota je dána vztahem \text{hustota}=\dfrac{\text{hmota}}{\text{objem}}. Hustotu vápníku lze zjistit určením hustoty jeho jednotkové buňky: například hmotnost obsažená v jednotkové buňce dělená objemem jednotkové buňky. Jednotková buňka Ca s centrovanou stěnou má osminu atomu v každém z osmi rohů \left(8\times \dfrac{1}{8}=1\text{ atom}\right) a polovinu atomu na každé ze šesti stěn \left(6\times \dfrac{1}{2}=3\text{ atomy}\right), celkem tedy čtyři atomy v jednotkové buňce.

Hmotnost jednotkové buňky lze zjistit takto:

\text{1 jednotková buňka Ca}\times \dfrac{\text{4 atomy Ca}}{\text{1 jednotková buňka Ca}}\times \dfrac{\text{1 mol Ca}}{6.022\times {10}^{23}\text{Atomy Ca}}\times \dfrac{40,078\text{g}}{\text{1 mol Ca}}=2.662\krát {10}^{-22}\text{g}

Objem jednotkové buňky Ca lze zjistit takto:

V={a}^{3}={(558,8\krát {10}^{-10}\text{cm})}^{3}=1.745\krát {10}^{-22}{\text{cm}}^{3}

(Všimněte si, že délka hrany byla převedena z pm na cm, abychom získali obvyklé jednotky objemu pro hustotu.)

Tedy hustota \text{Ca}=\dfrac{2,662\times {10}^{-22}\text{g}}{1,745\times {10}^{-22}{\text{cm}}^{3}}={\text{1.53 g/cm}}^{3}

Zkontrolujte si své znalosti

Stříbro krystalizuje ve struktuře FCC. Délka hrany jeho jednotkové buňky je 409 pm.

1. Jaký je atomový poloměr Ag v této struktuře?
2. Vypočítejte hustotu Ag.

Ukázat řešení

1. 144 pm
2. 10. Jaký je atomový poloměr Ag v této struktuře?5 g/cm3

Všeobecně je jednotková buňka definována délkami tří os (a, b a c) a úhly (α, β a γ) mezi nimi, jak je znázorněno na obrázku 10. Jak je znázorněno na obrázku 10? Osy jsou definovány jako délky mezi body v prostorové mřížce. Z toho vyplývá, že osy jednotkové buňky spojují body se shodným okolím.

Obrázek 10. Jednotková buňka je definována délkami svých tří os (a, b a c) a úhly (α, β a γ) mezi osami.

Existuje sedm různých mřížkových soustav, z nichž některé mají více než jeden typ mřížky, celkem čtrnáct různých jednotkových buněk, které mají tvary znázorněné na obrázku 11.

Obrázek 11. Mřížková soustava. Existuje sedm různých mřížkových soustav a 14 různých jednotkových buněk.

Struktury iontových krystalů

Iontové krystaly se skládají ze dvou nebo více různých druhů iontů, které mají obvykle různé velikosti. Uspořádání těchto iontů do krystalové struktury je složitější než uspořádání atomů kovů, které mají stejnou velikost.

Většina jednoatomových iontů se chová jako nabité koule a jejich přitažlivost pro ionty s opačným nábojem je ve všech směrech stejná. V důsledku toho vznikají stabilní struktury iontových sloučenin (1) když jsou ionty jednoho náboje obklopeny co největším počtem iontů opačného náboje a (2) když jsou kationty a anionty ve vzájemném kontaktu. Struktury jsou určeny dvěma hlavními faktory: relativní velikostí iontů a poměrem počtu kladných a záporných iontů ve sloučenině.

Obrázek 12. Kationty mohou obsadit dva typy otvorů mezi anionty: oktaedrické nebo tetraedrické otvory.

V jednoduchých iontových strukturách obvykle nacházíme anionty, které jsou obvykle větší než kationty, uspořádané v nejtěsnějším poli. (Jak jsme viděli dříve, další elektrony přitahované ke stejnému jádru zvětšují anionty a menší počet elektronů přitahovaných ke stejnému jádru zmenšuje kationty ve srovnání s atomy, z nichž jsou vytvořeny). Menší kationty obvykle obsazují jeden ze dvou typů děr (nebo mezer), které zůstávají mezi anionty. Menší z děr se nachází mezi třemi anionty v jedné rovině a jedním aniontem v sousední rovině. Čtyři anionty obklopující tuto díru jsou uspořádány v rozích čtyřstěnu, proto se díra nazývá tetraedrická díra. Větší typ díry se nachází uprostřed šesti aniontů (tří v jedné vrstvě a tří v sousední vrstvě) umístěných v rozích oktaedru; tato díra se nazývá oktaedrická díra. Oba tyto typy děr jsou znázorněny na obrázku 12.

V závislosti na relativní velikosti kationtů a aniontů mohou kationty iontové sloučeniny zaujímat tetraedrické nebo oktaedrické díry, jak je znázorněno na obrázku 13.

. Relativně malé kationty obsazují tetraedrické otvory a větší kationty obsazují oktaedrické otvory. Pokud jsou kationty příliš velké na to, aby se vešly do oktaedrických otvorů, mohou anionty zaujmout otevřenější strukturu, například jednoduché krychlové uspořádání. Větší kationty pak mohou obsadit větší krychlové otvory umožněné otevřenějším uspořádáním.

Obrázek 13. Vpravo jsou všechny mřížové body fialové. Velikost kationtu a tvar díry obsazené sloučeninou spolu přímo souvisí.

Pro každý aniont existují dvě tetraedrické díry v poli aniontů HCP nebo CCP. Sloučenina, která krystalizuje v nejbližším uspořádání aniontů s kationty v tetraedrických otvorech, může mít maximální poměr kationtů k aniontům 2:1; všechny tetraedrické otvory jsou zaplněny v tomto poměru. Příkladem jsou Li2O, Na2O, Li2S a Na2S. Sloučeniny s poměrem menším než 2:1 mohou také krystalizovat v nejtěsnějším uspořádání aniontů s kationty v tetraedrických otvorech, pokud tomu odpovídají velikosti iontů. V těchto sloučeninách však některé tetraedrické otvory zůstávají volné.

Poměr oktaedrických děr k aniontům ve struktuře HCP nebo CCP je 1:1. Jaký je vzorec selenidu lithného? Sloučeniny s kationty v oktaedrických dírách v nejbližším uspořádání aniontů tedy mohou mít maximální poměr kationtů k aniontům 1:1. Například v NiO, MnS, NaCl a KH jsou všechny oktaedrické otvory zaplněny. Poměr menší než 1:1 se vyskytuje, když některé z oktaedrických otvorů zůstávají prázdné.

V jednoduchém krychlovém poli aniontů je pro každý aniont v poli jeden krychlový otvor, který může být obsazen kationtem. V CsCl a v dalších sloučeninách se stejnou strukturou jsou obsazeny všechny kubické otvory. Polovina kubických otvorů je obsazena v SrH2, UO2, SrCl2 a CaF2.

Různé typy iontových sloučenin často krystalizují ve stejné struktuře, pokud jsou relativní velikosti jejich iontů a jejich stechiometrie (dvě hlavní vlastnosti určující strukturu) podobné.

Jednotkové buňky iontových sloučenin

Mnoho iontových sloučenin krystalizuje s kubickými jednotkovými buňkami a my tyto sloučeniny použijeme k popisu obecných vlastností iontových struktur.

Když je iontová sloučenina složena z kationtů a aniontů podobné velikosti v poměru 1:1, tvoří obvykle jednoduchou kubickou strukturu. Příkladem je chlorid cesný, CsCl (znázorněný na obrázku 14), jehož Cs+ a Cl- mají poloměry 174 pm, resp. 181 pm. Můžeme si to představit tak, že chloridové ionty tvoří jednoduchou krychlovou jednotkovou buňku s cesiovým iontem uprostřed; nebo jako ionty cesia tvořící jednotkovou buňku s chloridovým iontem uprostřed; nebo jako jednoduché krychlové jednotkové buňky tvořené ionty Cs+ překrývající jednotkové buňky tvořené ionty Cl-. Ionty cesia a chloridové ionty se dotýkají podél tělesných úhlopříček jednotkových buněk. V každé jednotkové buňce je přítomen jeden cesiový ion a jeden chloridový ion, což dává stechiometrii l:l požadovanou vzorcem pro chlorid cesný. Všimněte si, že ve středu buňky není žádný mřížkový bod a CsCl není BCC strukturou, protože cesiový ion není totožný s chloridovým iontem.

Obrázek 14. Vpravo se objeví hromada krychlí s fialovými koulemi, mezi nimiž se na jedné straně zobrazují malé zelené koule. Iontové sloučeniny s podobně velkými kationty a anionty, jako je CsCl, obvykle tvoří jednoduchou krychlovou strukturu. Lze je popsat jednotkovými buňkami s kationty v rozích nebo s anionty v rozích.

Řekli jsme, že umístění mřížkových bodů je libovolné. To ilustruje alternativní popis struktury CsCl, v němž jsou mřížkové body umístěny ve středech cesiových iontů. V tomto popisu jsou cesiové ionty umístěny na mřížkových bodech v rozích buňky a chloridový ion se nachází ve středu buňky. Obě jednotkové buňky se liší, ale popisují identickou strukturu.

Pokud se iontová sloučenina skládá z kationtů a aniontů v poměru 1:1, které se výrazně liší velikostí, obvykle krystalizuje s jednotkovou buňkou FCC, jako je znázorněno na obrázku 15.

. Příkladem je chlorid sodný, NaCl, jehož Na+ a Cl- mají poloměry 102 pm, resp. 181 pm. Můžeme si to představit tak, že chloridové ionty tvoří buňku FCC, přičemž sodíkové ionty se nacházejí v oktaedrických otvorech uprostřed okrajů buňky a ve středu buňky. Ionty sodíku a chloridu se vzájemně dotýkají podél okrajů buňky. Jednotková buňka obsahuje čtyři ionty sodíku a čtyři chloridové ionty, což dává stechiometrii 1:1, kterou vyžaduje vzorec, NaCl.

Obrázek 15. Iontové sloučeniny s anionty, které jsou mnohem větší než kationty, například NaCl, obvykle tvoří FCC strukturu. Lze je popsat jednotkovými buňkami FCC s kationty v oktaedrických otvorech.

Kubická forma sulfidu zinečnatého, blend zinečnatý, rovněž krystalizuje v jednotkové buňce FCC, jak je znázorněno na obrázku 16. Tato struktura obsahuje sulfidické ionty na mřížkových bodech FCC mřížky. (Uspořádání sulfidových iontů je totožné s uspořádáním chloridových iontů v chloridu sodném.) Poloměr zinečnatého iontu je jen asi 40 % poloměru sulfidového iontu, takže tyto malé ionty Zn2+ jsou umístěny ve střídavých tetraedrických otvorech, tj. v jedné polovině tetraedrických otvorů. V jednotkové buňce jsou čtyři zinečnaté ionty a čtyři sulfidové ionty, což dává empirický vzorec ZnS.

Obrázek 16. Znázornění krychle. ZnS, sulfid zinečnatý (nebo zinkový blende) tvoří jednotkovou buňku FCC se sulfidovými ionty v mřížkových bodech a mnohem menšími ionty zinku, které zaujímají polovinu tetraedrických otvorů ve struktuře.

Jednotková buňka fluoridu vápenatého, podobně jako na obrázku 17, je také jednotkovou buňkou FCC, ale v tomto případě jsou kationty umístěny v mřížkových bodech; ekvivalentní ionty vápníku jsou umístěny v mřížkových bodech mřížky FCC. Všechna tetraedrická místa ve FCC mřížce vápenatých iontů jsou obsazena fluoridovými ionty. V jednotkové buňce jsou čtyři vápenaté ionty a osm fluoridových iontů, což dává poměr vápníku a fluoru l:2, jak vyžaduje chemický vzorec CaF2. Při pozorném zkoumání obrázku 17 zjistíme jednoduché krychlové uspořádání fluoridových iontů s vápenatými ionty v jedné polovině krychlových otvorů. Strukturu nelze popsat pomocí prostorové mřížky bodů na fluoridových iontech, protože všechny fluoridové ionty nemají identické prostředí. Orientace čtyř vápenatých iontů kolem fluoridových iontů se liší.

Obrázek 17. Fluorid vápenatý, CaF2, tvoří FCC jednotkovou buňku s vápenatými ionty (zelené) v mřížkových bodech a fluoridovými ionty (červené), které obsazují všechna tetraedrická místa mezi nimi.

Výpočet iontových poloměrů

Známe-li délku hrany jednotkové buňky iontové sloučeniny a polohu iontů v buňce, můžeme vypočítat iontové poloměry pro ionty ve sloučenině, pokud předpokládáme tvary a kontakty jednotlivých iontů.

Příklad 5: Výpočet iontových poloměrů

Délka hrany jednotkové buňky LiCl (struktura podobná NaCl, FCC) je 0.514 nm neboli 5,14 Å. Předpokládejte, že iont lithia je dostatečně malý, takže chloridové ionty jsou v kontaktu, jako na obrázku 15, vypočítejte iontový poloměr pro chloridový iont.

Poznámka: Délková jednotka angström, Å, se často používá k vyjádření rozměrů v atomovém měřítku a odpovídá 10-10 m.

Zobrazit řešení

Na stěně jednotkové buňky LiCl se chloridové ionty dotýkají přes úhlopříčku stěny:

Kreslíme-li pravoúhlý trojúhelník na stěnu jednotkové buňky, vidíme, že délka úhlopříčky je rovna čtyřem chloridovým poloměrům (jeden poloměr od každého rohového chloridu a jeden průměr – což se rovná dvěma poloměrům – od chloridového iontu ve středu stěny), takže d = 4r. Z Pythagorovy věty máme:

{\text{a}}^{2}+{\text{a}}^{2}={\text{d}}^{2}

což dává:

\levá(0,514\text{ nm{}}pravá)^{2}+\levá(0.514\text{ nm}\right)^{2}={\left(4r\right)}^{2}=16{r}^{2}

Solving this gives:

r=\sqrt{\dfrac{{(0.514\text{nm})}^{2}+{(0.514\text{nm})}^{2}}{16}}=\text{0.182 nm} (1,82 Å) pro poloměr Cl-

Zkontrolujte si znalosti

Délka hrany jednotkové buňky KCl (struktura podobná NaCl, FCC) je 6,28 Å. Za předpokladu kontaktu aniont-kationt podél hrany buňky vypočítejte poloměr draselného iontu. Poloměr chloridového iontu je 1,82 Å.

Zobrazit řešení

Poloměr draselného iontu je 1,33 Å.

Je důležité si uvědomit, že hodnoty iontových poloměrů vypočítané z délky hran jednotkových buněk závisí na mnoha předpokladech, jako je například dokonalý kulový tvar iontů, které jsou v nejlepším případě aproximací. Proto jsou takové vypočtené hodnoty samy o sobě přibližné a srovnání nelze příliš posouvat. Přesto se tato metoda ukázala jako užitečná pro výpočet iontových poloměrů z experimentálních měření, jako jsou rentgenová krystalografická stanovení.

Rentgenová krystalografie

Velikost jednotkové buňky a uspořádání atomů v krystalu lze určit z měření difrakce rentgenového záření krystalem, tzv. rentgenové krystalografie. Difrakce je změna směru šíření, kterou zažívá elektromagnetická vlna, když narazí na fyzikální překážku, jejíž rozměry jsou srovnatelné s rozměry vlnové délky světla. Rentgenové záření je elektromagnetické záření s vlnovou délkou přibližně stejně dlouhou, jako je vzdálenost mezi sousedními atomy v krystalech (řádově několik Å).

Při dopadu svazku monochromatických rentgenových paprsků na krystal jsou jeho paprsky rozptýleny atomy uvnitř krystalu do všech směrů. Když se rozptýlené vlny putující stejným směrem setkají, dochází k interferenci, což je proces, při kterém se vlny kombinují a v závislosti na tom, do jaké míry jsou maxima kombinujících se vln od sebe vzdálena, dochází buď ke zvýšení, nebo snížení amplitudy (intenzity) (viz obrázek 18).

Obrázek 18. U světelných vln, které zaujímají stejný prostor, dochází k interferenci a jejich kombinací vznikají vlny s větší (a) nebo menší (b) intenzitou v závislosti na vzdálenosti jejich maxim a minim.

Pokud jsou rentgenové paprsky určité vlnové délky, λ, rozptýleny atomy v sousedních krystalových rovinách vzdálených od sebe vzdálenost d, mohou projít konstruktivní interferencí, pokud je rozdíl vzdáleností, které obě vlny urazily před jejich kombinací, celočíselným faktorem, n, vlnové délky. Tato podmínka je splněna, když úhel rozptýleného paprsku θ souvisí s vlnovou délkou a meziatomovou vzdáleností podle rovnice:

n{\lambda }=2d\text{sin}\theta

Tento vztah je znám jako Braggova rovnice na počest W. H. Bragga, anglického fyzika, který tento jev poprvé vysvětlil. Na obrázku 19 jsou znázorněny dva příklady difraktovaných vln ze dvou stejných krystalových rovin. Obrázek vlevo znázorňuje vlny difraktované pod Braggovým úhlem, což vede ke konstruktivní interferenci, zatímco obrázek vpravo ukazuje difrakci a jiný úhel, který nesplňuje Braggovu podmínku, což vede k destruktivní interferenci.

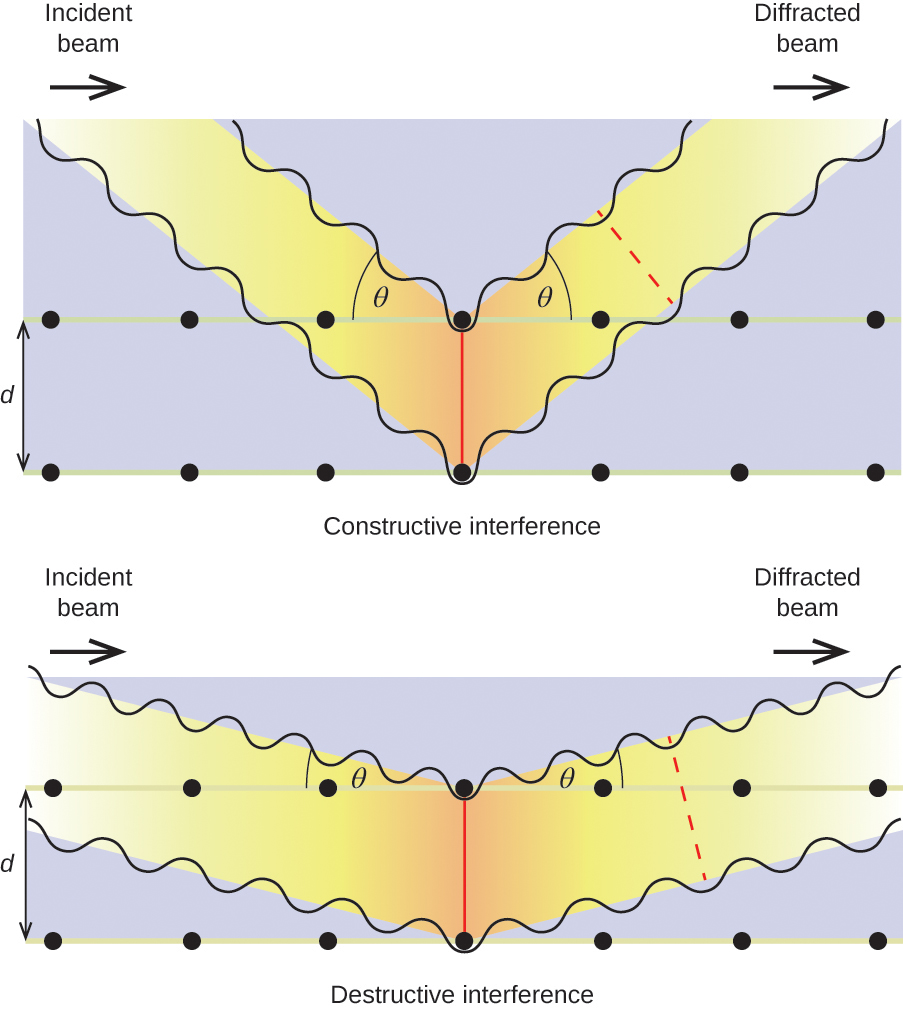
Obrázek 19. Difrakce rentgenového záření rozptýleného atomy v krystalu umožňuje určit vzdálenost mezi atomy. Horní obrázek znázorňuje konstruktivní interferenci dvou rozptýlených vln a výslednou difraktovanou vlnu vysoké intenzity. Spodní obrázek znázorňuje destruktivní interferenci a výslednou difraktovanou vlnu s nízkou intenzitou.

K měření úhlů, pod kterými se rentgenové paprsky difraktují při interakci s krystalem, jak je popsáno výše, lze použít rentgenový difraktometr, například ten, který je znázorněn na obrázku 20. Difraktometrem lze měřit úhly, pod kterými se rentgenové paprsky difraktují. Z takových měření lze pomocí Braggovy rovnice vypočítat vzdálenosti mezi atomy, jak je ukázáno v následujícím příkladovém cvičení.

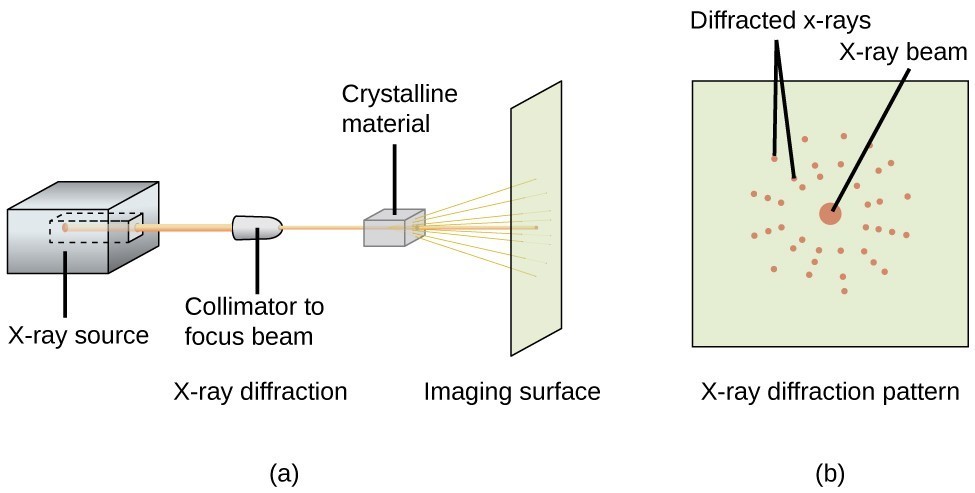
Obrázek 20. V difraktometru (a) dopadá svazek rentgenových paprsků na krystalický materiál a vytváří rentgenový difrakční obrazec (b), který lze analyzovat za účelem určení krystalické struktury.

Zápis z filmu „Celebrating Crystallography – An animated adventure“ si můžete prohlédnout zde (otevře se v novém okně).

Portrét chemika: Rosalind Franklinová, rentgenová krystalografka

Obrázek 21. Tato ilustrace ukazuje rentgenový difrakční obrázek podobný tomu, který Franklinová našla při svém výzkumu. (kredit: National Institutes of Health)

Objev struktury DNA v roce 1953 Francisem Crickem a Jamesem Watsonem je jedním z největších úspěchů v historii vědy. V roce 1962 jim byla udělena Nobelova cena za fyziologii nebo lékařství spolu s Mauricem Wilkinsem, který poskytl experimentální důkaz struktury DNA. K tomuto monumentálnímu úspěchu neocenitelně přispěla britská chemička Rosalind Franklinová svou prací při měření rentgenové difrakce DNA. Na počátku své kariéry se Franklinová věnovala výzkumu struktury uhlí, který se ukázal jako užitečný pro britské válečné úsilí. Poté, co počátkem 50. let 20. století přesunula své zaměření na biologické systémy, Franklinová spolu s doktorandem Raymondem Goslingem zjistila, že DNA se skládá ze dvou forem: dlouhého, tenkého vlákna, které vzniká za mokra (typ „B“), a krátkého, širokého vlákna, které vzniká za sucha (typ „A“). Její rentgenové difrakční snímky DNA (obr. 21) poskytly zásadní informace, které Watsonovi a Crickovi umožnily potvrdit, že DNA tvoří dvojitou šroubovici, a určit podrobnosti o její velikosti a struktuře.

Franklinová také prováděla průkopnický výzkum virů a RNA, která obsahuje jejich genetickou informaci, a odhalila nové informace, které radikálně změnily soubor poznatků v této oblasti. Poté, co Franklinová onemocněla rakovinou vaječníků, pokračovala v práci až do své smrti v roce 1958 ve věku 37 let. Mezi mnohá posmrtná uznání její práce patří to, že Chicagská lékařská fakulta Finchovy univerzity zdravotnických věd změnila v roce 2004 svůj název na Univerzitu medicíny a vědy Rosalindy Franklinové a jako oficiální logo univerzity přijala obrázek jejího slavného rentgenového difrakčního snímku DNA.

Glosář

těleso kubické (BCC) pevná látka: krystalická struktura, která má kubickou jednotkovou buňku s mřížkovými body v rozích a ve středu buňky

těleso kubické jednotkové buňky: Je to krychle obsahující mřížkové body v každém rohu a ve středu krychle

Braggova rovnice: rovnice, která vyjadřuje úhly, pod nimiž se rentgenové záření rozptyluje od atomů v krystalu

koordinační číslo: počet atomů nejbližších k danému atomu v krystalu nebo k centrálnímu atomu kovu v komplexu

cubic closest packing (CCP): Krystalová struktura, v níž jsou roviny těsně zabalených atomů nebo iontů uspořádány jako řada tří střídajících se vrstev s různou relativní orientací (ABC)

difrakce: krystalická struktura sestávající z krychlové jednotkové buňky s mřížkovými body v rozích a uprostřed každé stěny

krychlová jednotková buňka s mřížkovými body v rozích a uprostřed každé stěny

: Je to krychle obsahující mřížkové body v každém rohu a ve středu každé stěny

hexagonální těsné uspořádání (HCP): krystalická struktura, v níž jsou těsně zabalené vrstvy atomů nebo iontů uspořádány jako řada dvou střídajících se vrstev s různou relativní orientací (AB)

díra: (také meziprostor) prostor mezi atomy v krystalu

izomorfní: mající stejnou krystalovou strukturu

oktaedrická díra: otevřený prostor v krystalu ve středu šesti částic umístěných v rozích oktaedru

jednoduchá kubická jednotková buňka: (také primitivní kubická jednotková buňka) jednotková buňka v jednoduché kubické struktuře

jednoduchá kubická struktura: krystalická struktura s kubickou jednotkovou buňkou s mřížovými body pouze v rozích

prostorová mřížka: všechny body v krystalu, které mají shodné prostředí

tetraedrická díra: tetraedrický prostor tvořený čtyřmi atomy nebo ionty v krystalu

jednotková buňka: nejmenší část prostorové mřížky, která se opakuje ve třech rozměrech a tvoří celou mřížku

rentgenová krystalografie: experimentální technika určování vzdáleností mezi atomy v krystalu měřením úhlů, pod kterými se rentgenové záření při průchodu krystalem difraktuje