K čemu jsou znakové tabulky?

V této chvíli je dobré se zeptat: jaký smysl má učit se o znakových tabulkách? Jednoduchá odpověď zní, že symetrii a s ní spojenou znakovou tabulku molekuly lze použít k interpretaci a předpovědi mnoha aspektů chemicky významných spektroskopií i vazeb. To si příště ukážeme na příkladu vibračních módů molekuly.

V laboratoři můžeme získat užitečná experimentální data pomocí infračervené (IR) a Ramanovy spektroskopie. Tato data lze porovnat s počtem IR a/nebo Ramanových aktivních pásů předpovězených na základě aplikace teorie grup a správné tabulky znaků. Matematika (teorie grup a maticová algebra), která stojí za tímto zpracováním, slouží jako pevný teoretický základ. Níže popsané manipulace fungují, protože všechny operace symetrie molekuly tvoří matematickou grupu a řídí se jejími pravidly. Jak již bylo uvedeno dříve, nemusíme ovládat tuto oblast matematiky, abychom mohli dobře využít znakové tabulky.

Stupně volnosti a vibrace v molekulách

Na začátku probereme stupně volnosti pro jednoduchou molekulu (vodu). Velmi rychle uvidíme, proč je velmi výhodné využít symetrii při zkoumání větších molekul.

Pro molekulu s „N“ atomy existuje 3N stupňů volnosti (nezapomeňte, že žijeme v trojrozměrném světě souřadnic x, y, z). U nelineární molekuly lze 3 stupně volnosti podepsat na translaci – pohyb tělesa jako celku (Tx, Ty, Tz) a 3 na rotaci (Rx, Ry, Rz). Zbývající pohyby atomů jsou posuny atomů z jejich středních poloh – těžiště se nemění. Tyto základní vibrace se označují jako „normální módy“. Nelineární molekula má tedy 3N-6 normálních módů. Pro vodu je počet normálních módů 3 (3 x 3 – 6 = 3). Pro lineární molekuly existuje 3N-5 normálních módů.

Pro vodu, která byla samozřejmě intenzivně studována, víme, že 3 vibrace jsou následující.

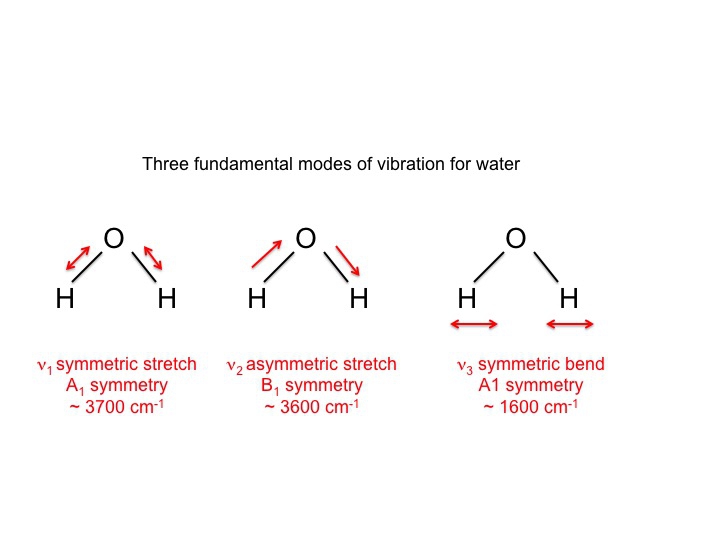
Symboly používané k popisu těchto módů (A1, B1) jsou stejné Mullikenovy symboly, se kterými jsme se setkali v naší diskusi o tabulkách znaků. Jinými slovy, vibrace, které jsou molekulovými vlastnostmi, lze popsat druhy symetrie nebo neredukovatelnými reprezentacemi. Ve skutečnosti velká část literatury týkající se vibrační spektroskopie používá tyto symboly jako zkrácený způsob sdělování informací.

Mělo by být zcela zřejmé, že počet vibrací rychle roste i při mírném zvýšení počtu atomů v molekule. Určování druhů vibrací prohlídkou (jak jsme to udělali u vody) je nyní mnohem obtížnější. Uvažujme například následující sloučeniny:

H2O 3 atomy 3 vibrace

PH3 4 atomy 6 vibrací

CO22- 4 atomy 6 vibrací

XeF4 5 atomů 9 vibrací

B2H6 8 atomů 18 vibrací

U diboranu (B2H6), který má symetrii D2h, by zjištění povahy a druhu symetrie všech 18 vibrací prohlídkou byl náročný úkol. Vyzbrojeni znakovou tabulkou pro D2h a znalostí symetrických vlastností je však úkol určit druh symetrie všech vibrací jednoduchý.

Pro případ vody bychom mohli uvést znakovou tabulku (C2v) se 3 vibracemi (ν1, v2, v3) uvedenými ve sloupci molekulových vlastností, jak je uvedeno níže. (ν = řecký symbol „nu“)

Všeobecně je však tento přístup nepraktický. Vezměme si například pyridin (C5H5N). Bodová skupina je také C2v, ale molekula má 11 atomů. Počet základních vibračních módů je 27 ( 3 x 11 – 6 = 27).

V tomto případě bychom museli sestavit tabulku znaků C2v zobrazující symetrie všech 27 vibrací. Z tohoto důvodu se vibrace obvykle do znakových tabulek nezahrnují. Místo toho je na uživateli (na vás), aby určil počet a typ vibrací (definovaných jejich druhy symetrií) pro všechny molekuly, se kterými se setká. Jak to uděláme, je popsáno níže.

Reduktivní reprezentace

Jak již bylo uvedeno, jednou z důležitých vlastností znakových tabulek je, že operace symetrie jsou členy matematické grupy a existují mezi nimi důležité vztahy. Obecně lze totéž říci o symetrických druzích neboli neredukovatelných reprezentacích molekulárních vlastností. Součin z kombinace znaků neredukovatelných zobrazení buď násobením, nebo sčítáním/odčítáním se také řídí pravidly grupy. Nová zobrazení již nejsou nejjednodušší možná a označují se jako „redukovatelná zobrazení“, protože je lze „redukovat“ na jejich složky.

Například pro vodu lze symetrie translace (Tx, Ty, Tz) získat přímo z tabulky znaků C2v. Jsou to A1, B1 a B2. Všechny tři tyto stupně volnosti můžeme znázornit pomocí zobrazení ΓT a můžeme zapsat níže uvedený výraz. (Γ = velké řecké písmeno „gama“).

ΓT = A1 + B1 + B2

Víme, že A1, B1 a B2 jsou pouze zkrácené zápisy pro druhy symetrie (neredukovatelná zobrazení). Můžeme tedy jednoduše zapsat znaky ΓT sečtením jednotlivých znaků pro A1, B1 a B2 z tabulky znaků C2v.

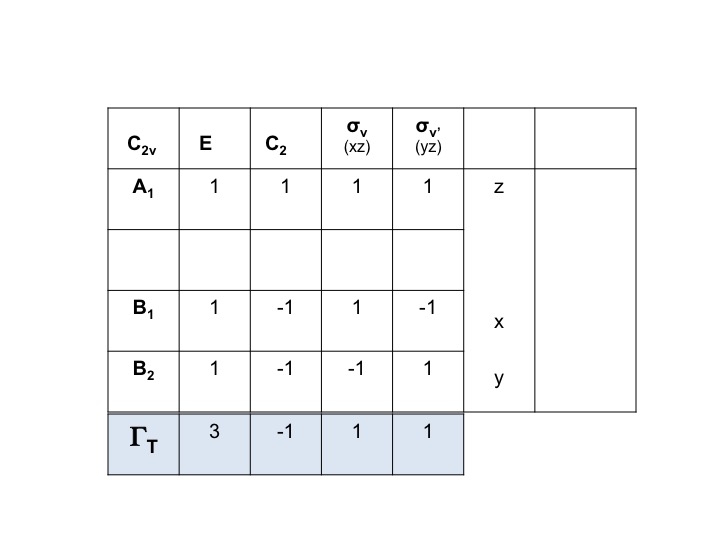
Tedy ΓT = 3 -1 1 1.

Toto je platné redukovatelné zobrazení a člen grupy C2v.

Podobným způsobem můžeme zapsat redukovatelné zobrazení pro všechny tři rotace a všechny vibrace.

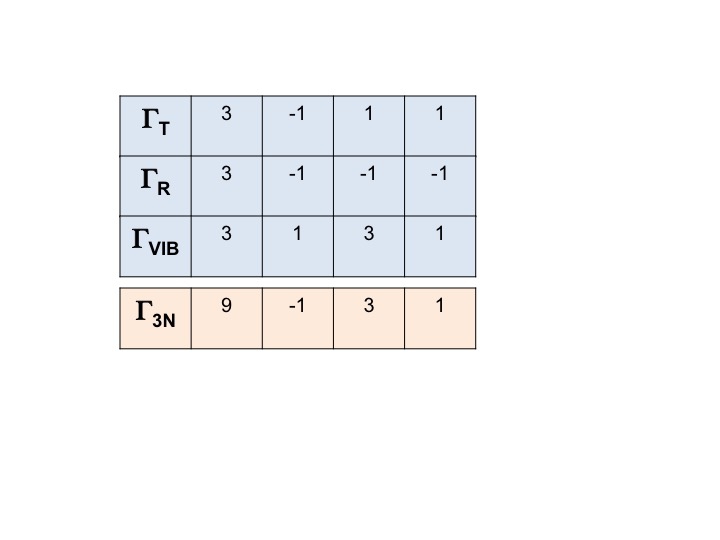
Zobrazení pro VŠECHNY stupně volnosti pro molekulu (3N) lze zapsat jako

Γ3N = ΓT + ΓR + ΓVIB

a redukovatelné zobrazení pro ni získáme prostým součtem znaků pro ΓT, ΓR a ΓVIB.

Γ3N = 9 -1 3 1

Zapište si to – přijde na to později!

Ačkoli množina znaků 9 -1 3 1 je platným členem grupy C2v, není při diskusi o molekulárních vlastnostech nijak zvlášť užitečná. To, co je skutečně zapotřebí, je jazyk zkrácených druhů symetrie (Mullikenovy symboly, A1, B1 atd.). Jinými slovy, chceme vyjádřit Γ3N v termínech A1, B1 atd. Z výše zahrnutých informací lze snadno ukázat inspekcí, že:

Γ3N = 3A1 +A2 + 3B1 +2B2

Dobrou zprávou je, že pro další složitější molekuly nemusíme tuto úlohu provádět inspekcí, protože:

1. Pro molekulu můžeme snadno vygenerovat Γ3N jako redukovatelné zobrazení (pokud známe její symetrii bodové skupiny).

2. Reduktivní zobrazení Γ3N můžeme snadno převést na součet jejích symetrických druhů (Mullikenových symbolů) pomocí „jednoduchého“ vzorce známého jako redukční vzorec.

Obecná metoda pro získání Γ3N

Krok 1

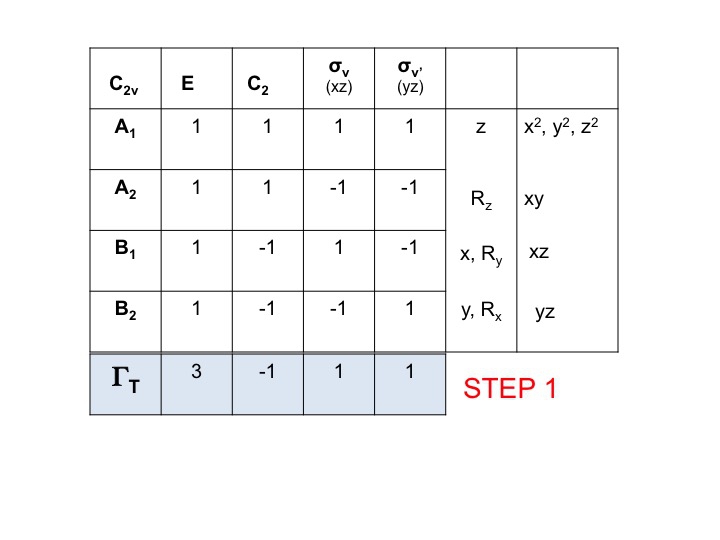
Vezměte tabulku znaků pro danou molekulu a přidejte řádek dole. V tomto řádku vytvořte redukovatelnou reprezentaci pro ΓT (nebo Γxyz), jak jsme to udělali výše, jednoduše přidáním znaků pro jednotlivé operace, které odpovídají molekulovým vlastnostem pro x, y a z. Pro C2v jsme si již ukázali, že to jsou znaky odpovídající A1, B1 a B2.

Krok 2

Přidejte pod ΓT další řádek a zapište počet atomů, které během každé operace symetrie NEMĚNÍ své umístění. Zde si uvědomíte, jak užitečná je skutečná sada molekulových modelů. K tomu budete také potřebovat vědět, kde se nacházejí prvky symetrie a jak operace symetrie ovlivňují molekulu. Samozřejmě už víte, jak to udělat, protože jste studovali Schönfliesův zápis a víte, jak přiřadit bodovou skupinu molekuly. V tabulce znaků jsou také všechny operace symetrie uvedeny podle tříd podél horního řádku.

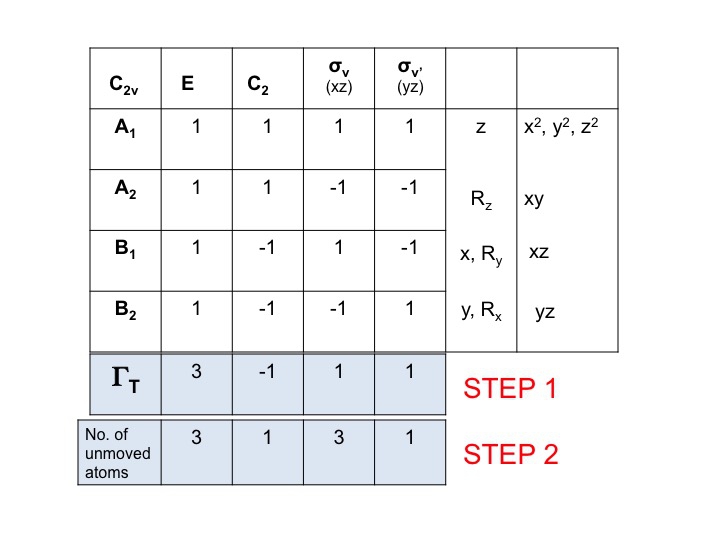
Tak pro vodu (3 atomy) jsou pod E 3 nepohyblivé atomy, ale pro C2 se pohybují oba H, ale protože atom O sedí na ose C2, nemění svou polohu, a tak pod sloupec C2 zapíšeme 1. V tabulce znaků jsou podél horního řádku uvedeny všechny operace symetrie. Nová množina čísel vygenerovaná v kroku 2 (3 1 3 1) je rovněž redukovatelným zobrazením v C2v a řídí se pravidly grupy.

Krok 3

V tomto kroku jednoduše vynásobíme dohromady znaky, které byly vygenerovány v krocích 1 a 2. V tomto kroku se nám podařilo vygenerovat znaky, které byly vygenerovány v krocích 2 a 3. Výsledkem (třetí řádek) je redukovatelné zobrazení pro Γ3N (nebo ΓTOT). Je to tak jednoduché.

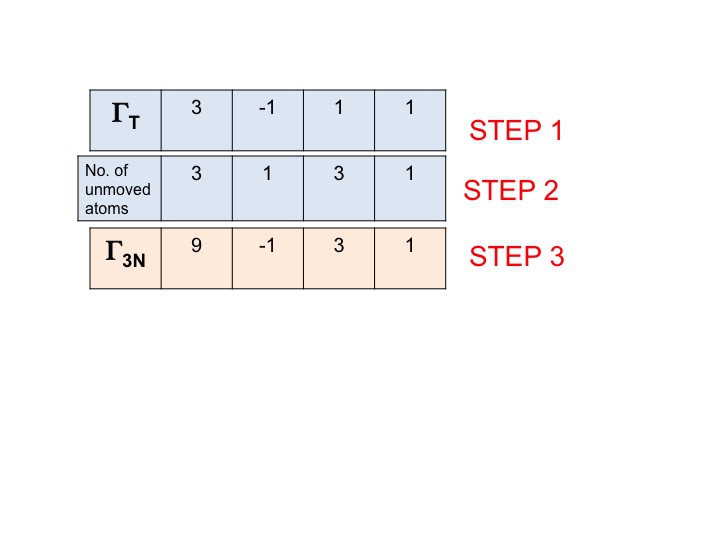
Všimněte si, že nová redukovatelná reprezentace (9 -1 1 3) je totožná s reprezentací pro Γ3N, kterou jsme získali dříve kontrolou.

Redukce redukovatelného zobrazení

K převodu KAŽDÉHO redukovatelného zobrazení na součet jeho neredukovatelných zobrazení (symetrických druhů nebo Mullikenových symbolů) použijeme redukční vzorec:

Tuto informaci snadno najdete v tabulce znaků:

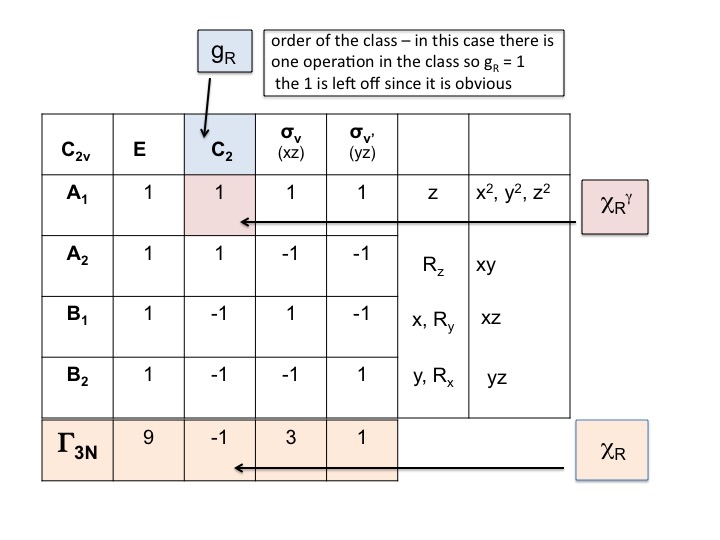
Zpět k našemu příkladu pro vodu: Bodová skupina C2v, řád (g) = 4

Reduktivní zobrazení pro Γ3N = 9 -1 3 1

Počet výskytů A1 v tomto zobrazení je tedy

aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3

takže Γ3N obsahuje 3 druhy symetrie A1. Počty ostatních druhů symetrie se vypočítají takto:

aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 přítomný druh A2

aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 B1 přítomný

aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1} = 2 2 B2 přítomný

Nyní můžeme psát Γ3N = 3A1 + A2 + 3B1 + 2B2 (přesně to, co jsme dostali „kontrolou“ výše. Nyní můžeme odečíst druhy symetrie pro translace a rotace a tím získáme počet a druhy symetrie základních modů kmitání. ΓT a ΓR lze získat přímo ze znakové tabulky.

Γ3N = 3A1 + A2 + 3B1 + 2B2

ΓT = A1 + B1 + B2

ΓR = A2 + B1 + B2

ΓVIB = Γ3N -. ΓT – ΓR = 2A1 +B1

Tři normálové vibrační módy pro vodu mají tedy symetrie A1, A1 a B1.

Máme nyní obecnou metodu pro určení všech základních modů vibrací pro molekulu a vyjádření těchto modů ve zkráceném jazyce Mullikenových symbolů. Toto je jedno z cvičení, ze kterého budete zkoušeni při zkoušce 1. Nejlepším způsobem, jak získat jistotu v této metodě, je procvičit si co nejvíce možných příkladů!

Další: Pravidla výběru