V sedmnáctém a zejména osmnáctém století, vedena jednak touhou porozumět přírodě, jednak snahou vyrobit balón, ve kterém by mohli létat (obr. 1), stanovila řada vědců vztahy mezi makroskopickými fyzikálními vlastnostmi plynů, tj. tlakem, objemem, teplotou a množstvím plynu. Přestože jejich měření nebyla podle dnešních měřítek přesná, dokázali určit matematické vztahy mezi dvojicemi těchto veličin (např. tlak a teplota, tlak a objem), které platí pro ideální plyn – hypotetickou konstrukci, které se skutečné plyny za určitých podmínek přibližují. Nakonec byly tyto jednotlivé zákony spojeny do jediné rovnice – zákona o ideálním plynu – která se vztahuje k plynným veličinám pro plyny a je poměrně přesná pro nízké tlaky a mírné teploty. Vezmeme v úvahu klíčový vývoj jednotlivých vztahů (z pedagogických důvodů ne zcela v historickém pořadí) a poté je spojíme do zákona o ideálním plynu.

Obrázek 1: Zákon o ideálním plynu. V roce 1783 došlo k prvnímu (a) letu balonu plněného vodíkem, (b) letu horkovzdušného balonu s posádkou a (c) letu balonu plněného vodíkem s posádkou. Když přistál balón plněný vodíkem znázorněný na obrázku (a), vyděšení vesničané z Gonesse jej údajně zničili vidlemi a noži. Start druhého z nich údajně v Paříži sledovalo 400 000 lidí.

Tlak a teplota: Gay-Lussacův zákon

Představte si, že naplníte pevnou nádobu připojenou k tlakoměru plynem a pak nádobu uzavřete tak, aby žádný plyn nemohl uniknout. Pokud nádobu ochladíme, plyn uvnitř se rovněž ochladí a pozorujeme, že jeho tlak klesá. Protože je nádoba pevná a těsně uzavřená, objem i počet molů plynu zůstávají konstantní. Pokud kouli zahřejeme, plyn uvnitř se zahřeje (Obrázek 2) a jeho tlak se zvýší.

Obrázek 2. Vliv teploty na tlak plynu: Když je horká deska vypnutá, je tlak plynu v kouli relativně nízký. Při zahřívání plynu se tlak plynu v kouli zvyšuje.

Tento vztah mezi teplotou a tlakem lze pozorovat pro jakýkoliv vzorek plynu uzavřený v konstantním objemu. Příklad experimentálních údajů o tlaku a teplotě je uveden pro vzorek vzduchu za těchto podmínek na obrázku 3. Zjistíme, že teplota a tlak jsou lineárně závislé, a pokud je teplota na kelvinově stupnici, pak jsou P a T přímo úměrné (opět při zachování konstantního objemu a molů plynu); pokud se teplota na kelvinově stupnici zvýší o určitý faktor, tlak plynu se zvýší o stejný faktor.

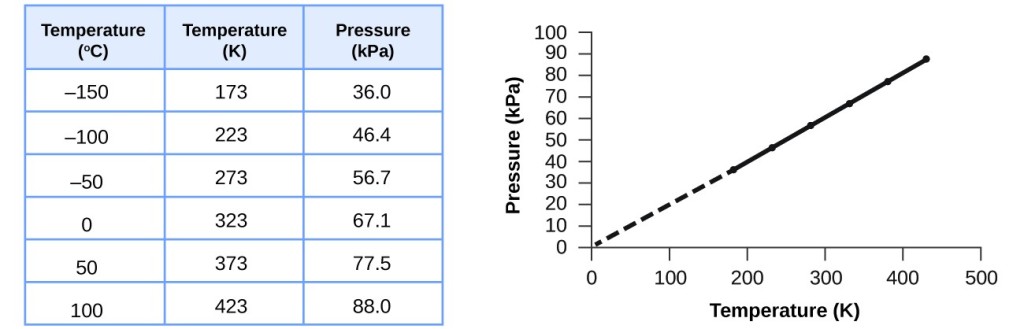
Obrázek 3. Pro konstantní objem a množství vzduchu jsou tlak a teplota přímo úměrné, pokud je teplota v kelvinech. (Při nižších teplotách nelze měření provádět z důvodu kondenzace plynu). Když tuto přímku extrapolujeme na nižší tlaky, dosáhneme tlaku 0 při teplotě -273 °C, což je 0 na kelvinové stupnici a nejnižší možná teplota, nazývaná absolutní nula.

Guillaume Amontons jako první empiricky stanovil vztah mezi tlakem a teplotou plynu (~1700) a Joseph Louis Gay-Lussac určil tento vztah přesněji (~1800). Z tohoto důvodu je vztah P-T pro plyny znám jako Gay-Lussacův zákon nebo Amontonsův zákon. Pod oběma názvy říká, že tlak daného množství plynu je přímo úměrný jeho teplotě na kelvinové stupnici, pokud je objem konstantní. Matematicky to lze zapsat takto:

\large P\propto T

\large P=\text{konstanta}\čas T

\large P=k\čas T

kde ∝ znamená „je úměrný“ a k je konstanta úměrnosti, která závisí na identitě, množství a objemu plynu.

\large\frac{{P}_{1}}{{T}_{1}}=\frac{{P}_{2}}{{T}_{2}}

Tato rovnice je užitečná pro výpočty tlaku a teploty uzavřeného plynu při konstantním objemu. Všimněte si, že pro jakékoliv výpočty podle plynového zákona musí být teploty na kelvinově stupnici (0 na kelvinově stupnici a nejnižší možná teplota se nazývá absolutní nula). (Všimněte si také, že existují nejméně tři způsoby, jak můžeme popsat, jak se mění tlak plynu při změně jeho teploty: Můžeme použít tabulku hodnot, graf nebo matematickou rovnici.)

Objem a teplota: Pokud naplníme balónek vzduchem a uzavřeme ho, obsahuje balónek určité množství vzduchu při atmosférickém tlaku, řekněme 1 atm. Vložíme-li balónek do chladničky, plyn uvnitř se ochladí a balónek se smrští (přestože množství plynu i jeho tlak zůstávají konstantní). Pokud balónek velmi ochladíme, velmi se smrští a po zahřátí se opět roztáhne.

Toto video ukazuje, jak ochlazení a zahřátí plynu způsobí zmenšení, respektive zvětšení jeho objemu.

Tyto příklady vlivu teploty na objem daného množství uzavřeného plynu při konstantním tlaku platí obecně: Objem se zvětšuje s rostoucí teplotou a zmenšuje s klesající teplotou. Údaje o závislosti objemu na teplotě pro vzorek 1 molu metanu při teplotě 1 atm jsou uvedeny a graficky znázorněny na obrázku 4.

Obrázek 4. Objem a teplota jsou lineárně závislé pro 1 mol metanu při konstantním tlaku 1 atm. Pokud je teplota v kelvinech, jsou objem a teplota přímo úměrné. Přímka se zastaví na teplotě 111 K, protože metan při této teplotě zkapalňuje; při extrapolaci protíná počátek grafu, což představuje teplotu absolutní nuly.

Závislost mezi objemem a teplotou daného množství plynu při konstantním tlaku je známá jako Charlesův zákon na počest francouzského vědce a průkopníka balónových letů Jacquese Alexandre Césara Charlese. Charlesův zákon říká, že objem daného množství plynu je přímo úměrný jeho teplotě na kelvinově stupnici při konstantním tlaku.

Matematicky to lze zapsat takto:

\velký V\propto T

\velký V=\text{konstanta}\cdot T

\velký V=k\cdot T

přičemž k je konstanta úměrnosti, která závisí na množství a tlaku plynu.

\large\frac{{V}_{1}}{{T}_{1}}=\frac{{V}_{2}}{{T}_{2}}

Objem a tlak: Boyleův zákon

Naplníme-li vzduchotěsnou injekční stříkačku částečně vzduchem, obsahuje stříkačka při konstantní teplotě, řekněme 25 °C, určité množství vzduchu. Pokud pomalu zatlačíme na píst při zachování konstantní teploty, plyn ve stříkačce se stlačí do menšího objemu a jeho tlak se zvýší; pokud píst vytáhneme, objem se zvětší a tlak se sníží. Tento příklad vlivu objemu na tlak daného množství uzavřeného plynu platí obecně. Zmenšením objemu uzavřeného plynu se zvýší jeho tlak a zvětšením jeho objemu se jeho tlak sníží. Ve skutečnosti platí, že pokud se objem zvětší o určitý faktor, tlak se o stejný faktor sníží a naopak. Údaje o objemu a tlaku vzorku vzduchu při pokojové teplotě jsou znázorněny v grafu na obrázku 5.

Obrázek 5. Když plyn zaujímá menší objem, působí vyšším tlakem; když zaujímá větší objem, působí nižším tlakem (za předpokladu, že se množství plynu a teplota nemění). Protože P a V jsou nepřímo úměrné, je graf závislosti 1/P na V lineární.

Na rozdíl od vztahů P-T a V-T nejsou tlak a objem navzájem přímo úměrné. Místo toho vykazují P a V nepřímou úměrnost: Zvyšování tlaku vede ke zmenšování objemu plynu. Matematicky to lze zapsat:

velký P\propto 1\text{/}V\text{ nebo }P=k\cdot 1\text{/}V\text{ nebo }P\cdot V=k\text{ nebo }{P}_{1}{V}_{1}={P}_{2}{V}_{2}

přičemž k je konstanta. Graficky je tento vztah znázorněn přímkou, která vznikne při vynesení inverzní hodnoty tlaku \velký\levý(\frac{1}{P}\pravý) v závislosti na objemu (V) nebo inverzní hodnoty objemu \velký\levý(\frac{1}{V}\pravý) v závislosti na tlaku (V). Grafy se zakřivenými čarami je obtížné přesně číst při nízkých nebo vysokých hodnotách proměnných a je obtížnější je použít při přiřazování teoretických rovnic a parametrů k experimentálním údajům. Z těchto důvodů se vědci často snaží najít způsob, jak svá data „linearizovat“. Pokud sestrojíme graf závislosti P na V, získáme hyperbolu (viz obrázek 6).

Závislost mezi objemem a tlakem daného množství plynu při konstantní teplotě poprvé publikoval anglický přírodovědec Robert Boyle před více než 300 lety. Je shrnut v tvrzení, které je dnes známé jako Boylův zákon:

Chemistry in Action: Dýchání a Boyleův zákon

Co děláte asi dvacetkrát za minutu po celý život, bez přestávky a často aniž byste si to uvědomovali? Odpovědí je samozřejmě dýchání neboli respirace. Jak to funguje? Ukazuje se, že zde platí plynové zákony. Vaše plíce přijímají plyn, který vaše tělo potřebuje (kyslík), a zbavují se odpadního plynu (oxidu uhličitého). Plíce jsou tvořeny houbovitou, pružnou tkání, která se při dýchání rozpíná a smršťuje. Při nádechu se stahuje bránice a mezižeberní svaly (svaly mezi žebry), čímž se rozšiřuje hrudní dutina a zvětšuje se objem plic. Zvětšení objemu vede ke snížení tlaku (Boyleův zákon). Tím dochází k proudění vzduchu do plic (z vysokého tlaku na nízký). Při výdechu se proces obrátí: Bránice a žeberní svaly se uvolní, hrudní dutina se stáhne a objem plic se zmenší, což způsobí zvýšení tlaku (opět Boyleův zákon) a vzduch proudí z plic ven (z vysokého tlaku na nízký). Poté se nadechujete a vydechujete znovu a znovu a tento cyklus Boyleova zákona se opakuje po zbytek vašeho života (Obrázek 7).

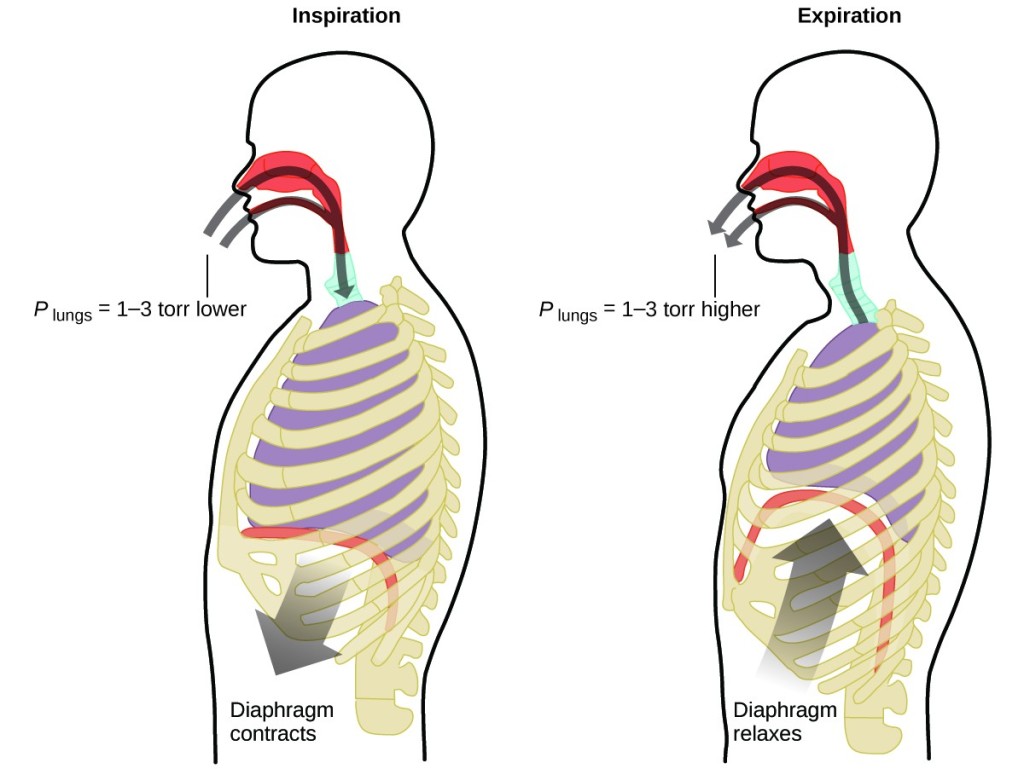
Obrázek 7. K dýchání dochází proto, že rozšiřování a smršťování objemu plic vytváří malé tlakové rozdíly mezi vašimi plícemi a okolím, což způsobuje nasávání vzduchu do plic a jeho vytlačování z plic.

Moly plynu a objem: Avogadrův zákon

Italský vědec Amedeo Avogadro vyslovil v roce 1811 hypotézu, která vysvětluje chování plynů a tvrdí, že stejný objem všech plynů měřený za stejných podmínek teploty a tlaku obsahuje stejný počet molekul. Postupem času byl tento vztah podpořen mnoha experimentálními pozorováními a vyjádřen Avogadrovým zákonem: Pro uzavřený plyn jsou objem (V) a počet molekul (n) přímo úměrné, pokud tlak a teplota zůstávají konstantní.

Ve tvaru rovnice je to zapsáno jako:

\large\begin{array}{ccccc}V\propto n& \text{nebo}& V=k\times n& \text{nebo}&. \frac{{V}_{1}}{{n}_{1}}=\frac{{V}_{2}}{{n}_{2}}\end{array}

Matematické vztahy lze určit i pro ostatní dvojice proměnných, například P versus n a n versus T.

Glosář

absolutní nula: teplota, při které by byl objem plynu podle Charlesova zákona nulový.

Avogadrův zákon: objem plynu při konstantní teplotě a tlaku je úměrný počtu molekul plynu

Boylův zákon: objem daného počtu molů plynu udržovaného při konstantní teplotě je nepřímo úměrný tlaku, za kterého se měří

Charlesův zákon: Objem daného počtu molů plynu je přímo úměrný jeho kelvinové teplotě při konstantním tlaku

Gay-Lussacův zákon: (také Amontonsův zákon) tlak daného počtu molů plynu je přímo úměrný jeho kelvinové teplotě, je-li objem konstantní