¿Para qué sirven las tablas de caracteres?
En este punto una buena pregunta es: ¿para qué sirve aprender sobre tablas de caracteres? La respuesta sencilla es que la simetría y la tabla de caracteres asociada de una molécula pueden utilizarse para interpretar y predecir muchos aspectos de las espectroscopias químicamente significativas, así como del enlace. Lo ilustraremos a continuación centrándonos en los modos vibracionales de una molécula.
En el laboratorio podemos reunir datos experimentales útiles utilizando espectroscopia infrarroja (IR) y Raman. Estos datos pueden compararse con el número de bandas activas IR y/o Raman predichas a partir de la aplicación de la teoría de grupos y la tabla de caracteres correcta. Las matemáticas (teoría de grupos y álgebra matricial) que subyacen a este tratamiento sirven de sólida base teórica. Las manipulaciones que se describen a continuación funcionan porque todas las operaciones de simetría de una molécula comprenden un grupo matemático y obedecen las reglas del grupo. Como se ha señalado anteriormente no tenemos que dominar esta área de las matemáticas para hacer un buen uso de las tablas de caracteres.
Grados de libertad y vibraciones en las moléculas
Aquí discutiremos inicialmente los grados de libertad para una molécula simple (agua). Rápidamente veremos por qué es muy beneficioso emplear la simetría cuando se investigan moléculas más grandes.
Para una molécula con «N» átomos hay 3N grados de libertad (recuerda que vivimos en un mundo tridimensional de coordenadas x, y, z). Para una molécula no lineal 3 grados de libertad pueden ser signados a traslaciones – movimiento de un cuerpo como un todo (Tx, Ty, Tz) y 3 a rotaciones (Rx, Ry, Rz). Los restantes movimientos de los átomos son desplazamientos de los átomos desde sus posiciones medias – el centro de gravedad no cambia. Estas vibraciones fundamentales se denominan «modos normales». Así, una molécula no lineal tiene 3N-6 modos normales. En el caso del agua, el número de modos normales es 3 (3 x 3 – 6 = 3). Para las moléculas lineales hay 3N-5 modos normales.
Para el agua, que por supuesto ha sido estudiada intensamente, sabemos que las 3 vibraciones son las siguientes.
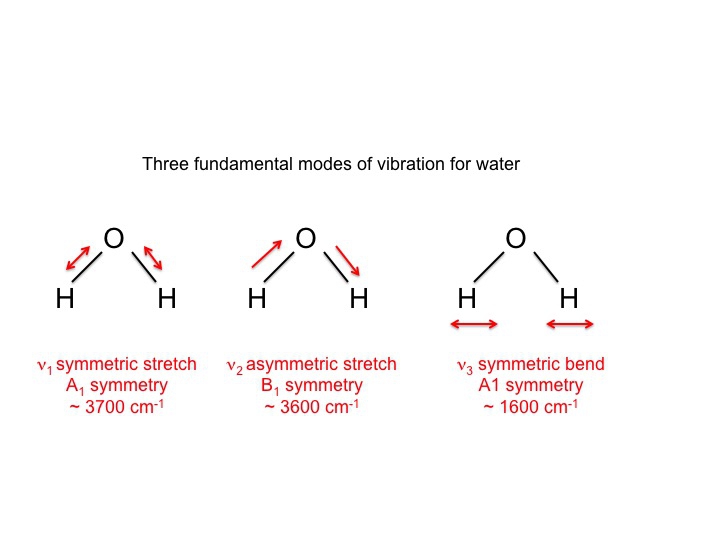
Los símbolos utilizados para describir estos modos (A1, B1) son los mismos símbolos de Mulliken que encontramos en nuestra discusión de las tablas de caracteres. En otras palabras, las vibraciones, que son propiedades moleculares, pueden describirse mediante especies de simetría o representaciones irreducibles. De hecho, gran parte de la literatura relacionada con la espectroscopia vibracional utiliza estos símbolos como una forma abreviada de comunicar la información.
Debería ser bastante obvio que el número de vibraciones aumenta rápidamente incluso con incrementos modestos en el número de átomos de la molécula. Determinar los tipos de vibraciones por inspección (como hicimos con el agua) se vuelve ahora mucho más difícil. Por ejemplo, consideremos los siguientes compuestos:
H2O 3 átomos 3 vibraciones
PH3 4 átomos 6 vibraciones
CO22- 4 átomos 6 vibraciones
XeF4 5 átomos 9 vibraciones
B2H6 8 átomos 18 vibraciones
Para el diborano (B2H6) que tiene simetría D2h averiguar la naturaleza y la especie de simetría de las 18 vibraciones por inspección sería una tarea desalentadora. Sin embargo, armados con la tabla de caracteres para D2h y el conocimiento de las propiedades de simetría, la tarea de determinar la especie de simetría de todas las vibraciones es sencilla.
Para el caso del agua podríamos presentar la tabla de caracteres (C2v) con las 3 vibraciones (ν1, v2, v3) listadas en la columna de propiedades moleculares como se muestra a continuación. (ν = símbolo griego «nu»)

Sin embargo, en general este enfoque es poco práctico. Tomemos como ejemplo la piridina (C5H5N). El grupo puntual es también C2v pero la molécula tiene 11 átomos. El número de modos fundamentales de vibración es 27 ( 3 x 11 – 6 = 27).
En este caso tendríamos que elaborar una tabla de caracteres C2v que muestre las simetrías de las 27 vibraciones. Por esta razón, las vibraciones no suelen incluirse en las tablas de caracteres. En su lugar, es el usuario (usted) quien debe determinar el número y el tipo de vibraciones (definidas por su especie de simetría) para cualquier molécula que se encuentre. A continuación se describe cómo hacerlo.
Representaciones Reducibles
Como se ha señalado anteriormente una de las propiedades importantes de las tablas de caracteres es que las operaciones de simetría son miembros de un grupo matemático y existen relaciones importantes entre ellas. En general, lo mismo puede decirse de las especies de simetría o representaciones irreducibles de las propiedades moleculares. Los productos de la combinación de los caracteres de las representaciones irreducibles, ya sea por multiplicación o adición/resta, también obedecen a las reglas del grupo. Las nuevas representaciones ya no son las más simples posibles y se denominan «representaciones reducibles» porque pueden ser «reducidas» a sus partes componentes.
Por ejemplo, para el agua las simetrías de las traslaciones (Tx, Ty, Tz) se pueden deducir directamente de la tabla de caracteres C2v. Son A1, B1 y B2. Podemos representar estos tres grados de libertad mediante una representación ΓT y podemos escribir la expresión siguiente (Γ = letra griega mayúscula «gamma»).
ΓT = A1 + B1 + B2
Sabemos que A1, B1 y B2 no son más que las notaciones abreviadas de las especies de simetría (representaciones irreducibles). Por lo tanto, podemos simplemente escribir los caracteres de ΓT sumando los caracteres individuales para A1, B1 y B2 de la tabla de caracteres C2v.
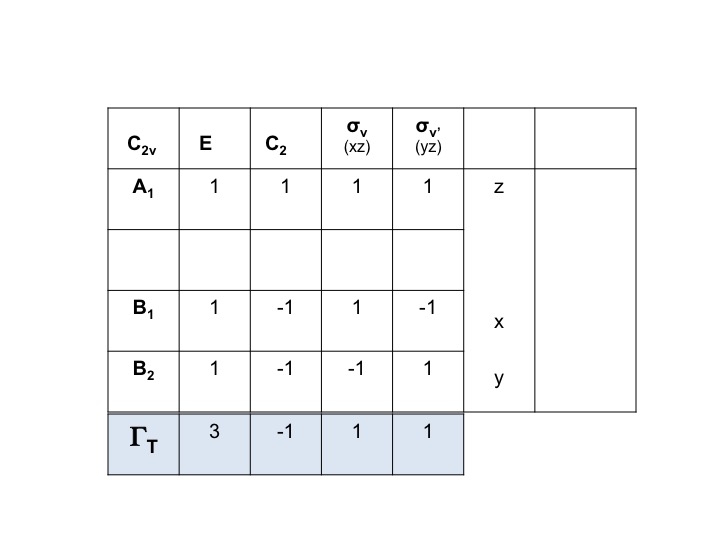
Así, ΓT = 3 -1 1 1.
Esta es una representación reducible válida y un miembro del grupo C2v.
De manera similar podemos escribir la representación reducible para las tres rotaciones y todas las vibraciones.
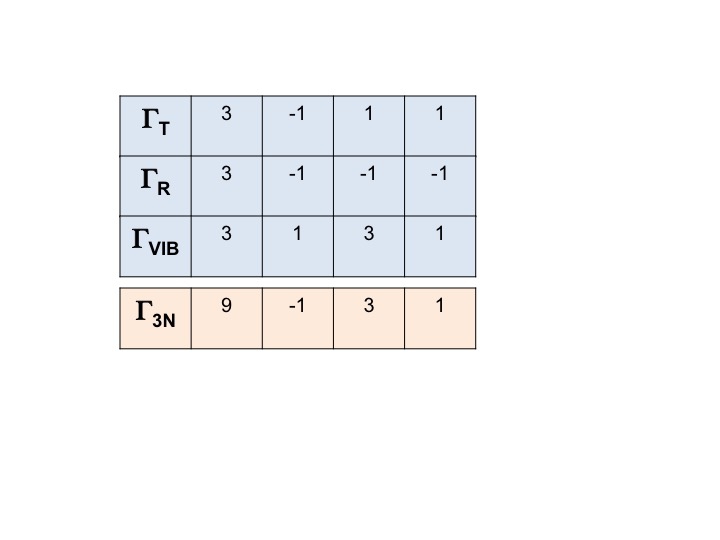
La representación para TODOS los grados de libertad de la molécula (3N) se puede escribir como
Γ3N = ΓT + ΓR + ΓVIB
y la representación reducible para ella se obtiene simplemente sumando los caracteres para ΓT, ΓR y ΓVIB.
Γ3N = 9 -1 3 1
Apunta esto – ¡surgirá más tarde!
Aunque el conjunto de caracteres 9 -1 3 1 es un miembro válido del grupo C2v no es particularmente útil cuando se discuten las propiedades moleculares. Lo que realmente se necesita es el lenguaje de las especies de simetría abreviada (símbolos de Mulliken, A1, B1, etc.). En otras palabras, queremos expresar Γ3N en términos de A1, B1, etc. A partir de la información cubierta anteriormente se puede demostrar fácilmente por inspección que:
Γ3N = 3A1 +A2 + 3B1 +2B2
La buena noticia es que para otras moléculas más complejas no tenemos que realizar esta tarea por inspección porque:
1. Podemos generar fácilmente Γ3N como representación reducible para una molécula (si conocemos su simetría de grupo puntual).
2. Podemos convertir fácilmente la representación reducible Γ3N en la suma de sus especies de simetría (símbolos de Mulliken) utilizando una fórmula «simple» conocida como fórmula de reducción.
Método general para obtener Γ3N
Paso 1
Toma la tabla de caracteres de la molécula y añade una fila en la parte inferior. En esta fila genera la representación reducible para ΓT (o Γxyz) como hicimos anteriormente, simplemente añadiendo los caracteres para cada operación que corresponden a las propiedades moleculares para x, y y z. Para C2v ya hemos demostrado que son los caracteres correspondientes a A1, B1 y B2.
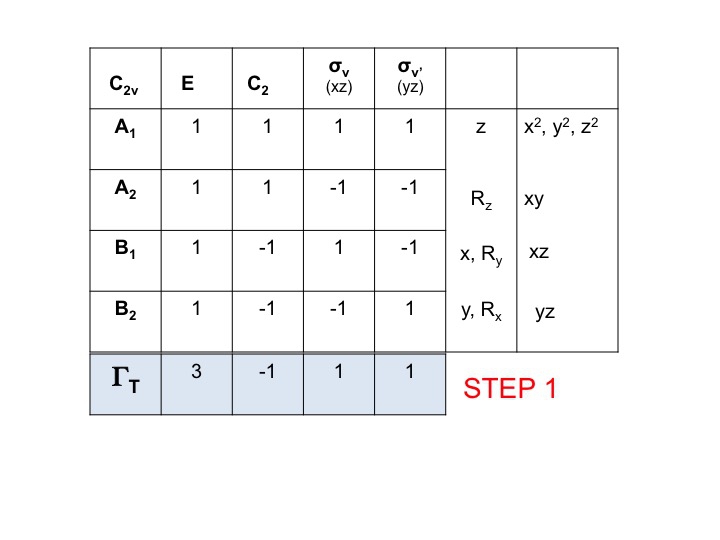
Paso 2
Agrega otra fila debajo de ΓT y anota el número de átomos que NO CAMBIAN su ubicación durante cada operación de simetría. Aquí es donde te das cuenta de lo útil que es un conjunto de modelos moleculares reales. Para ello también necesitarás saber dónde están los elementos de simetría y cómo afectan las operaciones de simetría a la molécula. Por supuesto, ya sabes cómo hacer esto porque has estudiado la notación de Schönflies y sabes cómo asignar el grupo de puntos de una molécula. La tabla de caracteres también tiene todas las operaciones de simetría listadas por clase a lo largo de la fila superior.
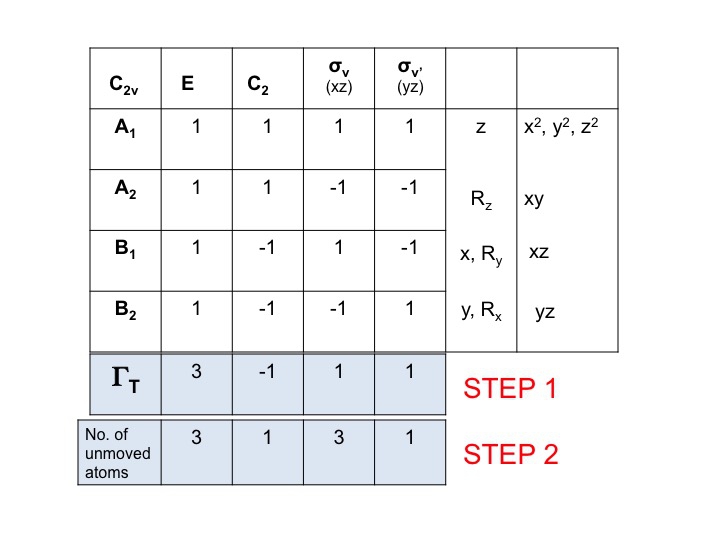
Así, para el agua (3 átomos) bajo E hay 3 átomos que no se mueven, pero para C2 ambos H se mueven pero como el átomo O se asienta en el eje C2 no cambia su ubicación y por eso registramos 1 bajo la columna C2. El nuevo conjunto de números generado en el paso 2 (3 1 3 1) es también una representación reducible en C2v y obedece a las reglas del grupo.
Paso 3
En este paso simplemente multiplicamos juntos los caracteres que se han generado en los pasos 1 y 2. El resultado (tercera fila) es la representación reducible para Γ3N (o ΓTOT). Es así de sencillo.
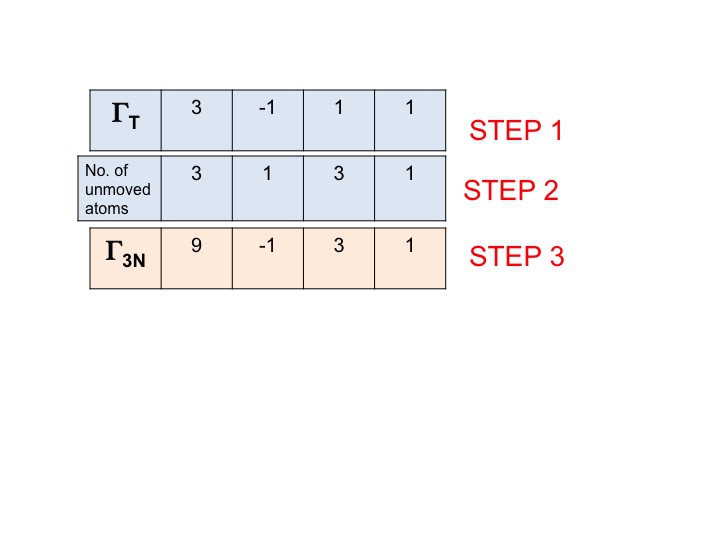
Notarás que la nueva representación reducible (9 -1 1 3) es idéntica a la representación para Γ3N que obtuvimos anteriormente por inspección.
Reducción de la representación reducible
Para convertir CUALQUIER representación reducible en la suma de sus representaciones irreducibles (especies de simetría o símbolos de Mulliken) utilizamos una fórmula de reducción:

Puedes encontrar fácilmente esta información en la tabla de caracteres:
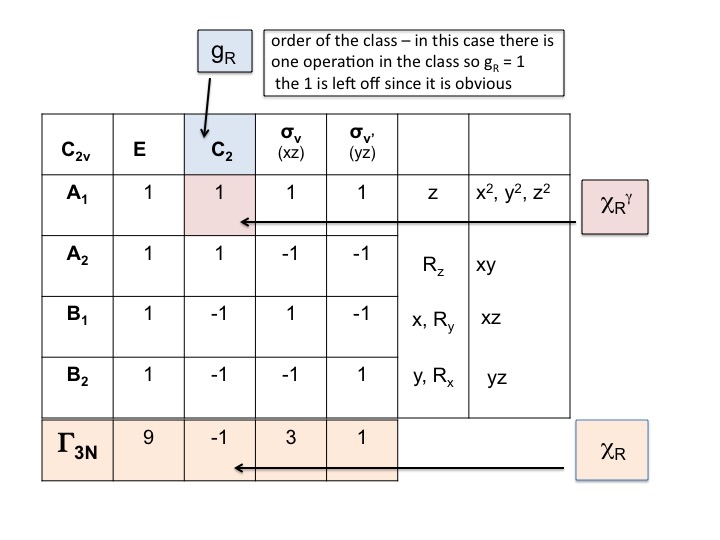
Volvemos a nuestro ejemplo del agua: Grupo puntual C2v, orden (g) = 4
La representación reducible para Γ3N = 9 -1 3 1
El número de veces que aparece A1 en esta representación es por tanto
aA1 = 1/4 { 1.1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3
por lo que Γ3N contiene 3 especies de simetría A1. Los números de las otras especies de simetría se calculan como sigue:
aA2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1).3 + 1.(-1).1 } = 1 un A2 presente
aB1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 B1 presente
aB2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1} = 2 2 B2 presente
Ahora podemos escribir Γ3N = 3A1 + A2 + 3B1 + 2B2 (exactamente lo que obtuvimos por «inspección» arriba. Ahora podemos restar las especies de simetría para las traslaciones y rotaciones y esto nos dará el número y las especies de simetría de los modos fundamentales de vibración. ΓT y ΓR se pueden obtener directamente de la tabla de caracteres.
Γ3N = 3A1 + A2 + 3B1 + 2B2
ΓT = A1 + B1 + B2
ΓR = A2 + B1 + B2
ΓVIB = Γ3N – ΓT – ΓR = 2A1 +B1
Así que los tres modos normales de vibración del agua tienen las simetrías A1, A1 y B1.
Ahora tenemos un método general para determinar todos los modos fundamentales de vibración de una molécula y expresar estos modos en el lenguaje abreviado de los símbolos de Mulliken. Este es uno de los ejercicios que se evaluarán en el Examen 1. La mejor manera de adquirir confianza con este método es practicar tantos ejemplos posibles como pueda
Siguiente: Reglas de selección